Тема уроку: Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною
Алгебра 9 клас
Методичні рекомендації до уроку
Тема уроку: Розв'язування систем (та сукупностей) лінійних нерівностей з однією змінною
Алгебра 9 клас
Методичні рекомендації до уроку
Тема уроку: Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною
Мета уроку: домогтися закріплення учнями змісту: поняття система нерівностей з однією змінною ( та поняття сукупності нерівностей з однією змінною); означення рівносильних нерівностей та властивостей рівносильних нерівностей; означення лінійної нерівності з однією змінною та схеми її розв’язування залежно від різних значень коефіцієнтів. Доповнити знання учнів уявленням про схему дій при розв’язуванні систем нерівностей з однією змінною, що зводиться до лінійних; схему дій при розв’язуванні сукупностей нерівностей з однією змінною, що зводяться до лінійних. Виробити вміння: виконувати дії відповідно до вивчених схем для розв’язування систем і сукупностей нерівностей з однією змінною. Продовжити роботу з вдосконалення вмінь: відтворювати зміст вивчених понять і алгоритмів; застосовувати їх для розв’язування вправ, що передбачають розв’язування лінійних нерівностей з однією змінною.
Компетентності, що формуються: математична – уміння оперувати числовою інформацією, розв’язувати вправи, що передбачають розв’язування лінійних нерівностей з однією змінною; ключові – інформаційно-цифрова; соціальна і громадянська; спілкування державною мовою; уміння вчитися впродовж життя.
Наочність та обладнання: опорний конспект, Т3Н.
Тип уроку: формування та закріплення знань, вироблення вмінь.
Хід уроку
- Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
- Перевірка домашнього завдання
Для здійснення поточного контролю засвоєння учнями матеріалу попередніх двох уроків пропонуємо учням виконати тестові завдання. Якість виконання завдань перевіряється одразу по виконанню роботи (для більшої ефективності роботи залучаємо Т3Н).
- Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Створити відповідні умови для мотивації навчальної діяльності учнів учитель може, як завжди , запропонувавши учням розв’язати конкретне практичне завдання, таке, що приводить їх до усвідомлення необхідності вивчення способів розв’язування як систем, так і сукупностей нерівностей з однією змінною ( це може бути , наприклад, завдання розв’язати нерівність з модулем або яка-небудь практична задача на розв’язання системи або сукупності нерівностей). Проаналізувавши запропоновану ситуацію, учні мають дійти висновку, що на практиці часто постає питання про відшукання всіх спільних розв’язків нерівностей з однією зміною ( розв’язання системи нерівностей ) або про відшукання всіх значень змінних, при яких хоча б одна з нерівностей перетворювалася на правильну ( розв’язання сукупності нерівностей ); а тому метою даного уроку є вивчення способів розв’язування систем нерівностей ( а також сукупностей нерівностей) з однією змінною.
- Актуалізація опорних знань та вмінь учнів
Усні вправи
-
При яких значеннях x дріб
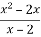 :
:
1)визначений; 2) дорівнює нулю?
- Розв’яжіть нерівність:
-
2х > 4; 2) –х ≥ 3; 3) –х ≤ 0; 4)
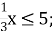 5)
5) 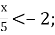 6)
6) 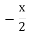 > 10.
> 10.
- Знайдіть переріз та об’єднання проміжків, що відповідають парі нерівностей:
- x ≥ 3 і х ≥ 5; 2) х ≥ 3 і х ≤ 5; 3) х ≥ 5 і х ≤ 3.
- Формування знань
План вивчення нового матеріалу
- Схема розв’язування систем нерівностей з однією змінною.
Приклади.
- Схема розв’язування сукупностей нерівностей з однією змінною.
Приклади.
Опорний конспект
|
Основні кроки розв’язування системи нерівностей з однією змінною 1. Розв’язуємо кожну нерівність системи. 2. Зображуємо множину розв’язків кожної нерівності на одній координатній прямій. 3. Знаходимо переріз числових проміжків , записуємо відповідь.
Приклад. Розв’яжемо систему нерівностей Розв’язання
Відповідь: Основні кроки розв’язування сукупності нерівностей з однією змінною
Приклад. Знайдемо розв’язок сукупності нерівностей
0 4 х
Відповідь:
|
Методичний коментар
Якщо на попередніх уроках в учнів сформувалися чіткі уявлення про зміст понять: система нерівностей з однією змінною, сукупність нерівностей з однією змінною, переріз та об’єднання числових проміжків, розв’язок нерівності з однією змінною , розв’язок системи та сукупності нерівностей з однією змінною, а також сталі навички розв’язування лінійних нерівностей з однією змінною та рівносильних перетворень нерівностей до виду лінійних, то при вивченні матеріалу даного уроку учні зазвичай не мають труднощів. Тому перед вивченням змісту нового матеріалу уроку доречно буде провести актуалізацію основних необхідних для цього знань та вмінь, яких учні набули протягом попередніх уроків (див. усні вправи вище).
Схеми , що пропонуються до опрацювання ( див. план), є стандартними і повністю відповідають уявленням учнів про зміст понять «що означає розв’язати систему нерівностей з однією змінною» і « що означає розв’язати сукупність нерівностей з однією змінною» (тому можна запропонувати скласти ці схеми самим учням). Проте приклади на застосування складених схем доречно підібрати таким чином, щоб учні побачили якомога більше різних випадків розв’язків цих систем або сукупностей (наприклад, коли одна з нерівностей не має розв’язків або коли одна з нерівностей має розв’язком усю числову пряму і т.д.). Також (якщо дозволяє час та рівень активності інтелектуальної діяльності учнів) на даному уроці можна розглянути «особливі випадки» систем лінійних нерівностей з однією змінною, які можна розв’язувати без допомоги числової прямої за правилами «більше більшого»(для системи нерівностей виду x>a, x>b). Наприкінці бесіди про застосування вивчених схем слід обговорити питання про застосування розв’язування систем нерівностей з однією змінною для розв’язування подвійних нерівностей (особливо у випадку, коли іншим способом, тобто через застосування властивостей числових нерівностей, це зробити буває досить проблематично).
- Формування вмінь
Усні вправи
- Чи є числа: - 4;0; 5 – розв’язками:
-
Системи
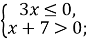 2) сукупності
2) сукупності 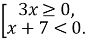
- На рисунках позначено множини розв’язків нерівностей системи. Чи є правильним запис множини розв’язків системи?
-
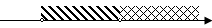 2)
2) 
3 4 х 0 3 х
![]() Розв’язків немає
Розв’язків немає
3) ![]() 4)
4) ![]()
( - 4; 1] ![]()
Письмові вправи
Вправи , запропоновані до розв’язання на уроці , мають відтворювати описані в теоретичній частині уроку ситуації, а саме передбачати закріплення знань та вироблення умінь застосовувати:
- Схему розв’язування систем нерівностей з однією змінною, що зводяться до лінійних нерівностей;
- Схему розв’язування сукупностей нерівностей з однією змінною, що зводяться до лінійних нерівностей ;
А також подальше вдосконалення вмінь учнів виконувати рівносильні перетворення нерівностей з однією змінною та розв’язування лінійних нерівностей з однією змінною.
Методичний коментар
Вправи , які слід розв’язати на уроці, мають бути спрямовані на вироблення навичок швидкого, послідовного та безпомилкового виконання дій:
а) розв’язування кожної нерівності системи (сукупності);
б) знаходження перерізу (об’єднання) знайдених проміжків.
При цьому вчителеві слід нагадати учням, що координатну пряму учні використовують для своєї зручності , тому рисунок відіграє допоміжну роль; це означає, що важливим у рисунку є лише правильне зображення послідовності розташування чисел на прямій. Після набуття певного досвіду з розв’язання систем нерівностей деякі учні усвідомлюють, що досить часто розв’язок системи нерівностей можна знаходити і без рисунка, тому від таких учнів не слід вимагати обов’язкового виконання рисунків. Для закріплення всіх контрольних моментів, відтворених у прикладах, які вчитель наведе при поясненні нового матеріалу, слід підібрати відповідні за змістом тренувальні вправи.
- Підсумки уроку. Рефлексія
На цьому етапі уроку, учні мають самі визначити, чи досягли вони своєї навчальної мети, щоб це зробити більш-менш обґрунтовано, пропонуємо їм цікаві вправи:
- Що означає «розв’язати систему нерівностей»? Опишіть дії, які треба виконати, щоб отримати розв’язок системи нерівностей.
-
Дано систему
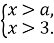 При яких a розв’язком системи є проміжок:
При яких a розв’язком системи є проміжок:
- (3;+∞); 2) (4;+∞); 3) (3;4)?
-
Дано систему:
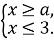 При яких a система має розв’язок:
При яких a система має розв’язок:
-
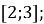 2) розв’язків немає; 3) x=5?
2) розв’язків немає; 3) x=5?
- Домашнє завдання
- Вивчити алгоритми виконання дій, складених та опрацьованих на уроці.
- Розв’язати завдання на формування навичок використання вивчених алгоритмів.
- Повторити означення та геометричний зміст модуля числа.


про публікацію авторської розробки
Додати розробку