Алгебра і початки аналізу "Похідна та її застосування"

КРИВОРІЗЬКА ЗАГАЛЬНООСВІТНЯ ШКОЛА І-ІІІ СТУПЕНІВ №69

КРИВОРІЗЬКОЇ МІСЬКОЇ РАДИ ДНІПРОПЕТРОВСЬКОЇ ОБЛАСТІ

Алгебра і початки аналізу

Тема: Похідна та її застосування

Виконала: вчитель математики

І. Червяченко

Кривий Ріг

Мета: Систематизувати і узагальнити знання учнів з даної теми. Розвивати пізнавальну активність, вміння виділяти головне у вивчаємому матеріалі, розвивати потребу в самоосвіті. Виховувати інтерес до предмету, вміння раціонально використовувати робочий час, виховувати науковий світогляд учнів.

Тип уроку: урок - семінар.

Обладнання: таблиці, портрети І.Ньютона, Г.Лейбніца.

Учні за два тижні до уроку отримали питання.

1.   Поняття про похідну.
2.   Похідні тригонометричних функцій.
3.   Геометричний зміст похідної.
4.   Похідна у фізиці і техніці.
5.   Метод інтервалів.
6.   Екстремальні точки.
7.   Дослідження функції на монотонність.

Крім того, учні по групам підбирали історичний матеріал про виникнення диференціального числення, про застосування похідної до дослідження функції та ін.

Хід уроку

1. Організаційний момент.
2. Повідомлення теми і мети уроку.

Сьогодні на уроці ми узагальнюємо і систематизуємо ваші знання, що стосуються теми з курсу математичного аналізу « Похідна та її застосування»

Під час семінару учні також познайомлять з історичними відомостями про виникнення диференціального числення.

3. Повторення та узагальнення теоретичних знань.

1. Заслухаємо короткий звіт учнів, які працювали над міні-проектом: «Поняття про похідну» ( за виступ – 2 бали ).

Видатний французький математик, політичний і військовий діяч Карно в свій час писав: « Нет ни одного открытия, которое осуществило бы в математике такой счастливый и быстрый переворот, который был сделан анализом безконечно малых; ни одно другое открытие не дало более простих и действенных способов для проникновения в познание законов природы».

До відкриття похідної незалежно один від одного прийшли два відомих учених – І. Ньютон і Г. Лейбніц наприкінці XVII ст. (демонструються портрети цих вчених). Проте ще задовго до цього Архімед розв’язав задачу на побудову дотичної до кривої та знайшов максимум функції у = х²(а-х). Різні задачі, що пов’язані з поняттям похідної, зустрічалися в працях Н. Тартальї, Кеплера, Р. Декарта.

І. Ньютон сформулював і розв’язав основну проблему математичного аналізу: «За даною довжиною шляху в будь-який момент часу знайти швидкість руху у вказаний час». І якщо він виходив із задач механіки, то Г. Лейбніц – із геометричних задач. У Г. Лейбніца первісним поняттям для похідної була дотична, а у Ньютона – швидкість.

Швидкість зміни функції f(х) у точці х₀ називається похідною функції f(х) у точці х₀.

За допомогою похідної можна вивчати не тільки швидкість механічного руху.

Так, силу можна вважати похідною роботи по переміщенню.

F=A¹(s)

Сила струму – похідна заряду за часом.

I =q¹(t)

Лінійна густина – похідна маси за довжиною.

P₁=m¹(l)

Теплоємність – похідна теплоти за температурою.

C=Q¹(t⁰)

Потужність – похідна роботи за часом.

N = F¹(t)

Коефіцієнт лінійного розширення – похідна від функції видовження стержня.

а=l¹(l)

2. Математичний кросворд навпаки.

Учні працюють в групах і складають запитання до запропонованих відповідей.

3.   Після підведення підсумків по кросворду і виставлення балів (максимальна кількість – 2 бали ), 7 учнів запрошуються до дошки і готують відповіді на теоретичні питання 1-7.
4. Завдання для інших учнів класу.

Використовуючи приведену таблицю, складіть план знаходження похідних нижче приведених функцій (1 бал за правильно виконане завдання).

 Завдання: Знайди похідну заданої функції.

1.   у = ln(cos x);
2.   у =e^sin7x;
3.   у = (х² - 4х + 9)¹⁰;
4.   у =tg2х – ctg⁶x;
5.   у = 8х¹⁴-9х⁵ -;
6.   у =;
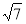7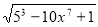.   у = sin¹²(5x + 7) .

5.   Заслуховуємо відповіді тих учнів, які готували біля дошки відповіді на теоретичні питання, причому за кожним із відповідаючих учнів закріплюється опонент, який в кінці коментує виступ і задає провокаційні питання. За повну і обґрунтовану відповідь - 2 бали.
6.   Слово надається учням групи № 2, які стисло знайомлять із своїм міні-проектом «Похідна у фізиці і техніці»

... основоположне поняття математичного аналізу - поняття функціональної залеж­ності , в якому, як у зародку, вже закладена вся ідея оволодіння явищами природи і процесами техніки за допомогою матема­тичного апарату.

О.Я.Хінчин

Поняття похідної виникло у XVII ст. у зв’язку з необхідністю розв’язувати деякі математичні і фізичні задачі. Задачу про побудову дотичної розв’язав Г. Лейбніц, про визначення миттєвої швидкості під час прямолінійного нерівномірного руху – І. Ньютон, який прийшов до поняття похідної, виходячи з положень механіки. Результати своїх досліджень він виклав у трактаті «Метод флексій», опублікованому в 1736р. Учений називав похідну флексією, а саму функцію – флюентою.

Похідна – це швидкість зміни функції. Нехай матеріальна точка рухається вздовж координатної прямої х за законом х = х(t). Тоді похідна від координати за часом у даний момент є швидкістю руху в цей момент часу. У цьому полягає її механічний зміст.

Поняття похідної як швидкості зміни функції використовується під час означень багатьох фізичних величин. Наприклад, похідна величини заряду за часом є сила струму; похідна потоку магнітної індукції за часом є електрорушійна сила індукції; похідна роботи за часом є потужність.

7.         Далі до дошки запрошуються ще 7 учнів і готують відповіді на запитання з теорії.
8.         Клас в цей час – робота в групах (завдання заздалегідь записані на переносній дошці).

1. Знайдіть стаціонарні точки функції: у = (х - 2)² - 3.
2. Запишіть рівняння дотичної до графіка функції у = 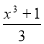в точці його перетину з віссю ОХ.
3.   В яких точках дотична до графіка функції у = 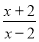утворює з віссю ОХ кут в 135^о.

Під час роботи в групах учні з’ясовують усі незрозумілі для себе питання, в разі потреби можуть отримати консультацію вчителя. Після обговорення результатів роботи, заслуховуємо відповіді учнів біля дошки.

9.         Міні-проект учнів III групи: «Застосування похідної до дослідження функції».

У світі не проходить нічого, в чому було б не видно змісту якого-небудь максимуму або мінімуму.

Л.Ейлер.

Іноді може виникнути запитання: для чого потрібна похідна? Може це лише «гола» теорія і все?

Як ми переконалися, похідна широко застосовується у фізиці. Крім того, з її допомогою проводять дослідження функції на зростання і спадання, екстремуми, найбільше і найменше значення. Із знаходженням найбільшого і найменшого значень функції пов’язана красива старовинна легенда, яка вперше зустрічається у безсмертному творінні «Енеїда». А для математика вона носить назву «задачі Дідони».

Фінікійська царівна Дідона, рятуючись від переслідувань свого брата, відправилась на захід вздовж берегів Середземного моря, де шукала собі пристановища. На узбережжі Туніської затоки вона почала вести переговори з Ярбом про купівлю для себе землі. І попросила вона зовсім небагато – стільки, скільки «можна обгородити шкірою з бика». І коли Ярб погодився, Дідона порізала шкуру бика на тоненькі смужки, зв’язала їх і обгородила ними велику територію, чого Ярб аж ніяк не чекав. На ній Дідона побудувала місто Карфаген, в якому прийняла згодом свою смерть.

Мовою математики задача звучить так: «Серед усіх замкнених кривих, що мають задану довжину, знайти ту, якою можна охопити найбільшу площу». Цю класичну задачу іноді називають ізопериметричною задачею Дідони. А кривою, що охоплює найбільшу площу, є круг – найдосконаліша, на думку Піфагора, плоска фігура.

Теорію задач на знаходження найбільших і найменших величин називають або теорією екстремальних задач, або теорією оптимізації. А якщо проблема стосується найкращого впливу на будь-які процеси і явища, якими людина, за певних умов, може керувати, то її відносять до розділу теорії екстремальних задач, що називається «оптимальним управлінням».

10.    Наступні 7 учнів працюють з теоретичним матеріалом біля дошки, а клас в цей час працює в парах. Цей вид роботи називається «Ти – мені, я – тобі». Суть його полягає в тому, що учень пропонує іншому учневі, з яким він працює в парі, завдання, тематику яких вказує вчитель. Після виконання роботи слідує взаємоперевірка, потім роботи здаються і вчитель ще раз перевіряє правильність як складеної умови завдання, так і його виконання. За запропоноване завдання - 1 бал, за виконання - 2 бали.
    1.   Задайте довільну функцію формулою і знайдіть область її визначення.
    2.   Область допустимих значень функції [ -9; 9], множина значень – [-4; 4]. Побудуйте графік функції, вкажіть проміжки монотонності, екстремуми функції.
    3.   Задайте формулою квадратичну функцію. Дослідіть її на монотонність і екстремуми.

Поки учні виконують завдання, вчитель заслуховує відповіді учнів біля дошки.

11.  НМШ

Задача, що пропонується для НМШ: Серед прямокутників, вписаних у коло, знайти прямокутник найбільшої площі.

Учні тієї групи, яка раніше запропонують план розв’язання задачі, отримують додатковий бал. Потім учень цієї групи оформлює розв’язок на дошці.

Розв’язання

Нехай сторони даного прямокутника дорівнюють х і у, а діаметр кола – 2R. За теоремою Піфагора маємо:

х² +у² = 4R²;

у =.

Площа прямокутника дорівнює:

S= xy=x , де х є [0;2R].

Знайдемо найбільше значення функції S(х) на відрізку [0;2R]:

1. S¹(x)=- = =.
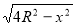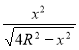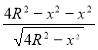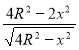2. S¹(x)=0, якщо

4R²-2x²=0,

2x²=4R²,

x2=2R²,

x=R.

3. S¹(0)=2R,

S(2R)=0,

S(R)= R*= R* R=2R².

Отже, для х=R функція S(х) набуває найбільшого значення, що дорівнює

у = ==R.

Тому шуканий прямокутник є квадратом зі стороною R. Відповідь. Квадрат зі стороною R.

12. Ми вже говорили про те, що основне призначення похідної – дослідження і побудова графіків функцій.

Вашій увазі пропонується графік функції:

у =

Учні 1 групи знаходять: ОДЗ, точки перетину з осями, досліджують функцію на парність (непарність).

2.     група знаходить у¹; досліджує функцію на монотонність.
3.     група знаходить у¹; досліджує функцію на екстремуми.

Потім прес-секретар від кожної групи знайомить учнів із своїми дослідженнями. Якщо все зроблено правильно, кожна група отримує 1 бал. Учні тієї групи, які раніше побудують графік, отримують додатково ще 1 бал.

IV. Самостійна робота по групам.

Група №1

1. Обчисліть похідну функції у(х) = 4х⁴ - Зх³ - 5х + 2 +tgх.
2.   Знайти стаціонарні точки функції f (х) = х² + 5х -107.
3.   Знайти найменше і найбільше значення функції f(х) =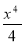+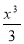- x² на відрізку [0;2].
4.   Дослідіть і побудуйте графік функції у = .
5.   Число 18 подати у вигляді суми двох невід’ємних доданків так, щоб добуток квадрата першого доданка і другого доданка був найбільшим.

Група №2

1. Обчисліть похідну функції f(х)=х⁵-Зх⁴+cos х.
2. Знайти зростання і спадання функції f(х) = 4х² - 15х +10.
3. Матеріальна точка рухається прямолінійно за законом: 5(7) = —Г + -Г

де s(t) – шлях у метрах, t – час у секундах.

4. Дослідіть і побудуйте графік функції у =
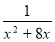
5.   Огорожею довжиною 24 м треба обгородити з трьох сторін прямокутну клумбу найбільшої площі. Знайти розміри клумби.

Група №3

1.               Обчисліть похідну функції f(х) = 5х²⁰ - 9х + 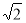+ctgх.
2.               Написати рівняння дотичної до графіка функції у=0,5х²-2х+2 в точці х₀=0.
3.               Розв язати методом інтервалів нерівність ≤0
4.               Знайти екстремуми функції у =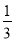sin x-1.
5.               Як зігнути кусок дроту довжиною l, щоб площа обмеженого ним прямокутника була найбільшою?

5.             Підсумки уроку.

Вчитель коментує роботу кожної із груп, знайомить з кількістю набраних балів за попередні види робіт, і повідомляє, що після перевірки самостійної роботи буде оголошено остаточну оцінку.

6.         Домашнє завдання.

1) Завершити роботу над навчальним портфоліо «Похідна навколо нас».

2) А: М. І. Сканаві. Збірник задач з математики №15.205; №15.146; №15.096;

    Б: №15.177; №15.228; №15.154.