ВИЗНАЧЕНИЙ ІНТЕГРАЛ ТА ЙОГО ЗАСТОСУВАННЯ. Інтегрований урок-семінар. 11 клас

ВИЗНАЧЕНИЙ ІНТЕГРАЛ ТА ЙОГО ЗАСТОСУВАННЯ. Інтегрований урок-семінар. 11 клас

 

Тема. Визначений інтеграл та його застосування

Мета: узагальнити та системати­зувати знання учнів з теми «Ви­значений інтеграл та його засто­сування»; розвивати логічне мис­лення учнів; показати значення математики в житті та розвитку різних наук; виховувати бачення цілісності світу.

Обладнання: плакати, рисунки, схеми алгоритмів, комп'ютерні програми обчислення визначених інтегралів, комп'ютери.

Підготовка: за тиждень до прове­дення семінару розбити клас на групи. Протягом тижня учні готу­ються за розподіленими завдан­нями.

 

ХІД УРОКУ-СЕМІНАРУ

 

...Природа формулює свої закони мовою математики.

Галілео Галілей

1. Організаційний етап

План семінару (2 години)

1.   Вступне слово вчителя. Оголо­шення теми та мети уроку.
2.    Історична довідка з розвитку питання про визначений інте­грал.
3.    Поняття визначеного інтеграла як границі інтегральної суми.
4.    Застосування визначених інте­гралів:

а) у геометрії (обчислення площ плоских фігур, об'ємів тіл обертання, де твірна — графік функції у = ƒ(х));

б) у фізиці (робота змінної сили та кількість електрики, що проходить через переріз про­відника за t с);

в) гідротехніці (відкачування води).

5.    Наближене обчислення інте­гралів:

а) методом прямокутників;

б) методом трапецій.

6.    Практична частина. Обчис­лення інтегралів за допомогою комп'ютера.
7.    Підбиття підсумків семінару.

2. Історична довідка з розвитку питання про визначений інтеграл

(Доповідь учня)

Початок інтегральному численню поклали задачі на обчислення площ плоских фігур, поверхонь та об'ємів тіл різної форми, а та­кож задачі на знаходження сумар­ного шляху під час нерівномірно­го руху.

Геометричні задачі розв'язували ще математики Стародавньої Греції. За допомогою розкладан­ня фігур на нескінченно тонкі шари на основі так званого мето­ду вичерпування було виведено формули для об'ємів піраміди, конуса, кулі.

8.   Математики XVII—XVIII ст. ще не користувалися поняттям границі. Вони говорили про «суму нескін­ченної кількості нескінченно ма­лих доданків». Саме на такій ос­нові німецький астроном, математик і механік Й. Кеплер (1571— 1630) у творах «Нова астрономія» (1609) та «Стереометрія винних бочок» (1615) обчислив ряд площ (площу еліптичного сектора, яка входить у формулювання другого закону Кеплера) та об'ємів різних тіл обертання. Ці дослідження продовжив італійський матема­тик Б. Кавальєрі (1598-1647).

Інтегральне та диференціальне числення тривалий час розвива­лися незалежно одне від одного. Англійський математик і філолог

9.                 Барроу (1630-1677) відкрив зв'язок між задачами знаходжен­ня площі і проведення дотичної до кривої. В загальному вигляді зв'язок між операціями інтегру­вання та диференціювання було встановлено англійським, фізи­ком і математиком І. Ньютоном (1643—1727) та німецьким мате­матиком і фізиком Г. Лейбніцом (1646—1716). Сучасне позначення інтеграла належить Лейбніцу, на­зва «інтеграл» — учневі Лейбніца, швейцарському математику Я. Бернуллі (1654-1705).

Значний внесок у вивчення по­няття інтеграла зробили україн­ські математики М. В. Остроград- ський (1801-1862), В. Я. Буня- ковський (1804-1889), Д. О. Граве (1863-1939), М. П. Кравчук (1892-1942) та інші.

3. Поняття визначеного інтегра­ла як границі інтегральної суми

За готовим рисунком (рис. 1) про­водимо фронтальне опитування. Основні етапи введення поняття визначення інтеграла записуються на дошці.

1). Яку фігуру називають криволінійною трапецією?

2). Які умови задовольняє функ­ція у = ƒ(х)?

3). Сформулюйте теорему Вейєрштрасса.

4). Яка фігура називається квадровною?

5). Дайте означення інтегральної суми для функції ƒ(х) на від­різку [а; b].

6). Що називається визначеним ін­тегралом? Як його позначають?

7). Чому дорівнює площа кри­волінійної трапеції?

8). Запишіть формулу Ньютона - Лейбніца для обчислення ви­значених інтегралів.

4. Застосування визначених інтегралів

Обчислення площ плоских фігур, об'ємів тіл обертання

а) Учні за готовими рисунками самостійно розв'язують задачі (усно).

Відповіді записують на окремих аркушах. Після виконання робо­ти (15 хв) проводиться самопе­ревірка за заздалегідь підготовле­ними за дошкою відповідями. Кожна правильна відповідь оці­нюється в 1 бал.

Завдання. Обчисліть площу за­штрихованої фігури.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

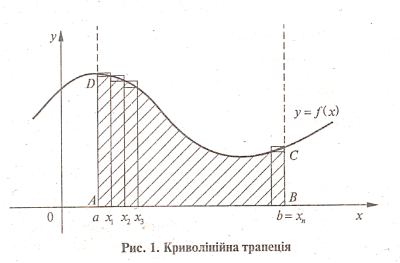
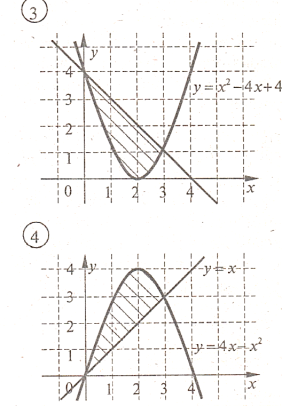
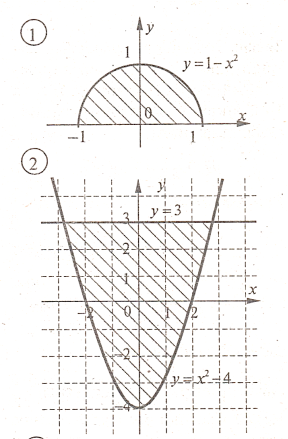
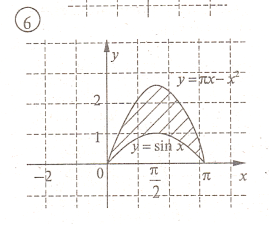
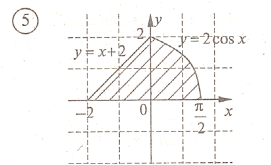
б). Задачі для письмового самостійного розв’язування (20 хв).

Задача 1. Знайдіть площу фігури, обмеженої віссю абсцис, параболою                у=2х² –х-1 і прямою х=-1 та віссю абсцис і цією параболою.

 

План розв’язування.

1.               Будуємо фігуру, площу якої треба знайти.

 

 

 

 

 

 

 

 

 

 

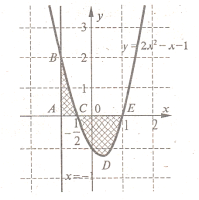
2.               S=S_ABC +S_CDE

 

3.                

 

Задача 2. Знайдіть площу фігури, обмеженої віссю абсцис, парабо­лою у--X^і -Зх і дотичною до цієї параболи в точці з абсцисою х = —1.

План розв'язування

1. Записуємо рівняння дотичної (;у = -х + 1).

1. Фігуру з шуканою площею схе­матично зображуємо і заштри­ховуємо на рисунку.
2. Площу шукаємо як

V — V - 9

*^{J —} ^ ABD ABC'

3. ABD — òðèêóòíèê ç êàòåòàìè BD = 2, AB = 2.

_BD₁AB_

ABD ~ j ~

4. ABC — êðèâîë³í³éíà òðàïåö³ÿ, ÿêà îáìåæåíà ãðàô³êîì ôóíê­ö³¿ ó = -õ

х= -1, х = 0, у = 0

0 у

Sak = J(-*² -3x)dx=-,

Відповідь. Б - —.

6

Після завершення роботи розв'я­зання задач обговорюються (за­здалегідь за дошкою або на плівці кодоскопа приготовлено пра­вильні розв'язання), проводиться взаємоперевірка. Кожна правиль­но розв'язана задача оцінюється в 3 бали.

Обчислення кількості електрики

За означенням, сила струму є по­хідною від кількості електрики 0 = 0(^г)>^де * ^{— час}' ^т°б^то

/(0-ОЧ0-

А тоді функція 0 - £?(ґ) є первіс­ною для функції / = /(ґ), тому кількість електрики, що прохо­дить через переріз провідника за час ґ, від ґ₂, можна знайти за фор- <2

мулою (? = |/(/)<#.

'і

Задача 3. Знайдіть кількість елек­трики, що проходить через попе­речний переріз провідника за 10 с, якщо сила струму зміню­ється за законом

/(/)=(4Г+І)(у0.

Розв'язання

л

і,

Є = |(4Г+1)Л = (2/²+Г)||₎⁰ = 210(КЛ).

Відповідь. 210 Кл.

Обчислення роботи змінної сили

Нехай тіло, що розглядається як матеріальна точка, рухається під дією змінної сили ^(х), напрям­леної вздовж осі Ох Знайдемо формулу для обчислення роботи під час переміщення з точки х = а у точку х = Ь.

Нехай Л(х) — робота під час пе­реміщення тіла з точки а в точку х. Надамо х приросту Ах Тоді А(х + Ах) -А(х) — робота, яка виконується силою Г(х) під час переміщення тіла з точки х у точ­ку х+Ах Коли Ах-ч>0, силу Г(х) на відрізку [х; х + А х] вва­жатимемо сталою, що дорівнює /■(*). Тому

А (х+ А х) - А(х) « ^(х) • А х,

звідки

4^х)

А х

або, за означенням похідної,

Л'(х) = /'(х).

Остання рівність означає, що Л(х) є первісною для функції

F(xy Тоді за формулою Ньюто­на—Лейбніца

ь

| х)ск = А(Ь)- А(а) =А(Ь) = А,

а

ОСКІЛЬКИ =0.

Отже, робота змінної сили /'(х) під час переміщення тіла з точки а

А

в точку Ьдорівнює А = | /'(х)^

а

Задача 4. Обчисліть роботу, яку треба виконати, щоб викачати воду з ями глибиною 4 м, що має квадратний переріз зі стороною

2 м. Густина води р = 10 —.

м³

Розв'язання

Спрямуємо вісь Ох вздовж діючої сили. Значення сили /'(х), що діє на переріз прямокутного парале­лепіпеда площею 4 м², визнача­ють вагою шару води, що знахо­диться вище від цього перерізу.

4 м

		X
У
1	1 1 1 1 1 1
	1 1 —		7
	2 м

Отже, Р(^х) -4р^(4 -х), де

хє[0;4],_Я = 9,84.

с

4

А = |4#р(4 - х)</х = о

4 / :

= 4£р|(4-х)оЬс=4£р 4х-—

О V ¹

= 4#р(16 —8) — 4 • 10³ -9,8-8 = = 313,6 ТО³ (Дж) = 3,1 • 10⁵ (Дж). Відповідь. =3,1-10⁵ Дж.

Обчислення шляху

Нехай точка рухається прямо­лінійно з деякою швидкістю V = у(7) залежно від часу Треба знайти шлях, який проходить точка за інтервал часу від ґ = 7", до ґ = Г₂.

Якщо швидкість руху стала і до­рівнює У₀ , то шлях 5 дорівнює до­бутку швидкості на час руху, тоб- то5 = У₀(Г₂ -І*).

Якщо ж швидкість не є сталою, то

S = \v(i)dt.

к=0

Точне значення шляху £ дістане­мо, якщо в цій сумі перейдемо до границі при Х(Г) -> 0,

Х(Т) = шах М_к, 0 < к < п -1.

Якщо функція неперервна на відрізку [7^і, ;Г₂], то ця границя дорівнюватиме інтегралу

Ті

Наведемо приклад застосування цієї формули.

Задача 5. Тіло рухається прямо­лінійно зі швидкістю, яка зміню

ється за законом V = 2/ +1

M

V у

Знайдіть шлях, який пройшло тіло за інтервал часу від г¹, = 1 с до ґ₂ =3с.

Розв'язання

Запишемо загальну формулу

't.

Підставимо у формулу свої зна­чення даної задачі

7 А „ N З

Завдання 2. Знайдіть число я, ко­ристуючись інтегралом

й!х

. ,1 п - arctg - —

^І0 4

(з 6 правильними знаками).

7. Підсумок уроку

Література

1. Каплан И. А. Практические занятия по высшей математике,— X., 1967.
2. Натансон И. П. Краткий курс высшей математики.— М., 1963.
3. Ивлев В. М. и др. Дидактические материалы по алгебре и началам анализа для 10 класса.— М.: Про­свещение, 1991.
4. Зморович В. Л. Математика. Посібник для факультативних за­нять.— К.: Радянська школа, 1972.
5. Шкіль. МЛ., Колесник Т. В., Хма­ра Т. М. Алгебра і початки ана­лізу,— К.: Освіта, 2003.
6. Вольвачев А Н., Крисевич В. С. Программирование на языке Пас­каль для ПЭВМ ЕС,- Минск, 1989.
7. Зуев Е. А. Язык программирова­ния Turbo Paskal.— M., 1992.
8. Скляров В. А. Знакомтесь: Пас­каль.— М., 1988.

/т

п *

ШЇКА

W.:» шкодах..України .

ПОГЛИБЛЕНЕ ВИВЧЕННЯ

Доведемо це.

Розглянемо Т — розбиття відрізка [Т,; Г₂ ] на п довільних частин точ­ками

7; =ґ₀</,<..</'* <?_і+1.■■</„_, <К=Т_г.

Вважатимемо, що швидкість на кожному проміжку \і_к;] стала

і дорівнює у(с_а), де с_к— деяка

точка відрізка \і_к \ Тоді шлях,

який проходить точка за час від ї=і_к до г = ґ_к+и наближено дорів­нює добутку

а шлях на відрізку [Г,; Г₂] дорів­нюватиме наближено

5 = |(2ґ + 1)Л =

= (9 +3-(1 + 1)) = 10 (м).

Відповідь. 5 = 10 м.

Наближені методи обчислення визначених інтегралів завжди по­глинають багато часу. Тому до­цільним буде використання об­числювальної техніки при засто­суванні методів прямокутників та трапецій.

5. Практична частина

Завдання 1. Обчисліть інтеграл