Алгебра-інформатика. Геометричні перетворення графіків тригонометричних функцій

Предмет: Алгебра                                                                                                  Вчитель: Околіта М. В.

Клас 10

Тема: Геометричні перетворення графіків тригонометричних функцій

Мета: удосконалити вміння та навички побудови графіків функцій за допомогою геометричних перетворень; ознайомлення студентів з можливостями використання прикладного програмного забезпечення для побудови графіків функцій;  розвивати логічне мислення, просторову уяву, а також творчі здібності студентів.

Тип уроку: систематизація та удосконалення знань, умінь і навичок.

Обладнання: комп’ютерний клас, матеріал з даної теми, плакати з графіками функцій, програмне забезпечення (MS Power Point, Advanced Grapher 2.2), дошка, маркери, лінійка, функціональні лінійки, індивідуальні картки.

Хід уроку

І. Організаційний етап.

- привітання;

- перевірка готовності учнів до уроку;

- налаштування на робочу обстановку;

ІІ. Фронтальне опитування.

На минулих уроках, ми вивчали і знаємо як зображаються графіки тригонометричних функцій.

Отже, потрібно дати відповіді на декілька запитань.

• Що є графіком функції y=sin x ? (синусоїда)
• Як з графіка функції y=sin x отримати графік y=cos x? (Треба виконати паралельне перенесення графіка y=sin x вліво на 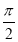одиниць, виходячи з рівняння .)
• Що є графіком функції y=tg x ? (Тангенсоїда.)
• Який період мають графіки y=sin x, y=cos x? (.)
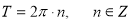• Які перетворення графіків функцій ви знаєте? (Симетрія, паралельне перенесення, деформація(стиск, розтяг).)

Відповідно до заданих запитань, ми з’ясували вигляд графіків, основних тригонометричних функцій. Але на практиці нам прийдеться будувати складніші графіки функцій.

Візьмемо за приклад таку функцію, яка описується даним рівнянням:

Щоб побудувати даний графік, потрібно виконати геометричне перетворення над графіком y=sin x.

III. Узагальнення знань з даної теми.

З даної бесіди, ви вже напевно зрозуміли, що темою нашого уроку буде: «Геометричні перетворення графіків тригонометричних функцій»

Проаналізуйте малюнок і назвіть геометричні перетворення, які виконуються для побудови графіків.

1)

2) - паралельне перенесення  графіка вправо на одиниць.

3) розтяг попереднього графіка вздовж осі ОХ  в 2 рази

4) паралельне перенесення останнього графіка

 вниз на одиницю.

Серед графіків, які зображено на малюнках 1- 4 назвіть графік функції:

 а) y=2sin x+2

б) y=2cos 2x 

в)

г)

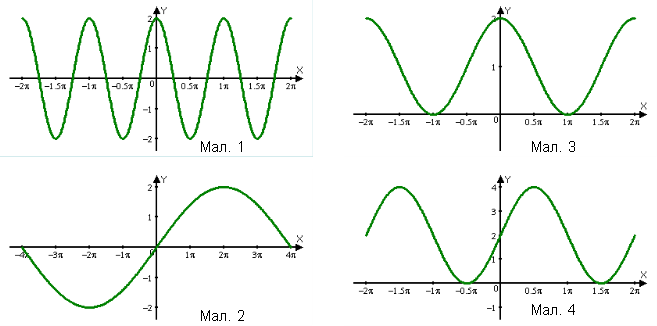
Відповідь:  а) мал.. 4;    б) мал.. 1;      в) мал.. 2;      г) мал.. 3.

Виконати в зошиті індивідуальне завдання з картки та перевірити правильність побудови за допомогою комп’ютера (програма Advanced Grapher 2.2).

 (Роздаються картки по одній на 2 студентів. Вони виконують побудову в зошиті. Пересідають за комп’ютери та будують ту саму функцію за допомогою запропонованої програми. Порівнюють результати).

V. Підсумки. (Оголошення оцінок). Д/з.:  

• 1. Побудувати графіки функцій:

 ; 

• 2. Повторити значення синусів,  косинусів, тангенсів від 0 до 180⁰.