Алгоритмічні картки як засіб активізації самостійної роботи учнів в умовах змішаного навчання
Алгоритмічні картки активізції самостійної роботи учнів в умовах змішаного навчання розроблені на весь курс алгебри у 8 класі. Алгоритмічні картки містять правила, формули, алгоритми, зразки розв'язання завдань, які у доступній формі показують учням як виконувати завдання, запропоновані для самостійного опрацювання, та різні завдання для закріплення і перевірки отриманих знань.
Навчаємось скорочувати
дроби за алгоритмом
Алгоритм
1.Розкладіть чисельник і знаменник дробу на множники (якщо в цьому є потреба).
2.Виділіть у чисельнику та знаменнику дробу найбільший спільний дільник.
3.Поділіть чисельник та знаменник дробу на найбільший спільний дільник.
ПРИКЛАДИ
Скоротіть дріб:
![]()
![]()
![]()
![]() 1)
1)![]() =2x2; 3)
=2x2; 3)![]() ;
;
![]()
![]()
![]()
![]()
![]()
![]() 2)
2)![]() ; 4)
; 4)![]() .
.
![]()
Варіант І Варіант ІІ
Скоротіть дріб: Скоротіть дріб:
1)![]() ; 1)
; 1) ![]() ;
;
2)![]() ; 2)
; 2)![]() ;
;
3)![]() ; 3)
; 3)![]() ;
;
4)![]() ; 4)
; 4)![]() ;
;
5)![]() . 5)
. 5)![]() .
.
![]()
Скорочення дробів
Як ми навчилися
користуватися алгоритмами
Варіант І
Знайдіть помилки у розв’язанні прикладів
та наведіть правильні розв’язання:
1)![]() ;
;
2)![]() ;
;
3)![]() ;
;
4)![]()
5)![]() .
.
Варіант ІI
Знайдіть помилки у розв’язанні прикладів
та наведіть правильні розв’язання:
1)![]() ;
;
2)![]() ;
;
3)![]() ;
;
4)![]() ;
;
5)![]() .
.
![]()
Скорочення дробів
Як ми навчилися користуватися алгоритмами
Варіант І
Виконайте скорочення дробів, заповнюючи пропуски:
1)![]() =
=![]() =
=![]() ;
;
2)![]() ;
;
3)![]() ;
;
4)![]() ;
;
5)![]() .
.
Варіант ІІ
Виконайте скорочення дробів, заповнюючи пропуски:
1)![]()
2)![]()
3)![]()
4)![]()
5)![]()
![]()
Скорочення дробів
Навчаємось додавати і віднімати дроби за алгоритмом
Алгоритм
1.Якщо дроби мають однакові ![]() , виконайте дії над чисельниками, а знаменник залиште без змін.
, виконайте дії над чисельниками, а знаменник залиште без змін.
2.Якщо дроби мають різні знаменники, зведіть їх до спільного знаменника таким чином:
1) знайдіть найменше спільне кратне (НСК) даних знаменників;
2) знайдіть додаткові множники до кожного дробу;
3) запишіть дроби зі спільним знаменником;
4) виконайте дії над одержаними дробами.
3. Спростіть результат, якщо це можливо.
ПРИКЛАДИ
Виконайте дії:
1![]()
2)![]() ;
;
3) .
.
![]() Варіант І Варіант ІІ
Варіант І Варіант ІІ
Виконайте дії Виконайте дії
1)![]() ; 1)
; 1) ![]() ;
;
2)![]() ; 2)
; 2) ![]() ;
;
3)![]() ; 3)
; 3)![]() ;
;
4)![]() ; 4)
; 4)![]() ;
;
5)![]() . 5)
. 5)![]() .
.
![]()
Додавання і віднімання
раціональних дробів
Як ми навчилися користуватися алгоритмом
Варіант І
Знайдіть помилки у розв’язанні прикладів
та наведіть правильні розв’язання:
1)![]() ;
;
2)![]() ;
;
3)![]()
4)![]() ;
;
5)![]() .
.
Варіант ІI
Знайдіть помилки у розв’язанні прикладів
та наведіть правильні розв’язання:
1)![]() ;
;
2)![]() ;
;
3)![]() ;
;
4)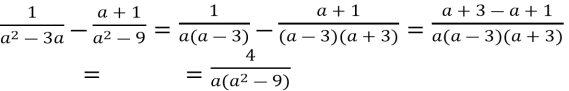 ;
;
5)![]() .
.
![]()
Додавання і віднімання
раціональних дробів
Ми свідомо застосовуємо набуті знання
Варіант І
Виконайте дії, заповнюючи пропуски:
1)![]() ;
;
2)![]() ;
;
3)![]() ;
;
4)![]() ;
;
5)![]() .
.
Варіант ІІ
Виконайте дії, заповнюючи пропуски:
1)![]() ;
;
2)![]() ;
;
3)![]() ;
;
4)![]() ;
;
5)![]() .
.
![]()
Додавання і віднімання
раціональних дробів
Навчаємося виконувати множення
і ділення дробів за алгоритмом
Алгоритм множення дробів
1.Чисельник першого дробу помножити на чисельник другого дробу.
2.Знаменник першого дробу помножити на знаменник другого дробу.
3.Перший добуток запишіть у чисельник дробу, а другий добуток – у знаменник дробу.
4.Скоротіть одержаний дріб, якщо це можливо.
Приклад
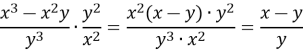
Алгоритм ділення дробів
1.Ділене залиште без змін.
2.Дію ділення замініть дією множення.
3.Дільник запишіть оберненим дробом.
4.Виконайте множення.
Приклад
![]() .
.
![]() Варіант І Варіант ІІ
Варіант І Варіант ІІ
Виконайте дії Виконайте дії
1)![]() ; 1)
; 1)![]() ;
;
2)![]() ; 2)
; 2)![]() ;
;
3)![]() ; 3)
; 3)![]() ;
;
4)![]() ; 4)
; 4)![]() .
.
![]()
Множення і ділення
раціональних дробів
Навчаємося виконувати піднесення
дробу до степеня за алгоритмом
Алгоритм
1.Піднесіть чисельник дробу до степеня.
2. Піднесіть знаменник дробу до степеня.
3. Перший одержаний вираз запишіть у чисельник нового дробу, а другий – у знаменник.
ПРИКЛАДИ
Піднесіть дріб до степеня:
![]() ;
;
2) ![]() =
=![]()
4) ( ![]()
![]()
Варіант І Варіант ІІ
Виконайте дії Виконайте дії:
1) ![]() ; 1)
; 1) ![]() ;
;
![]() 2)
2)![]() ;
;
3) ![]() ; 3)
; 3) ![]() ;
;
4) ![]() . 4)
. 4) ![]() .
.
![]() Піднесення раціонального
Піднесення раціонального
дробу до степеня
Як ми навчилися користуватися алгоритмом
Варіант І
Знайдіть помилки у розв’язанні прикладів та наведіть правильні розв’язання:
![]() )=3x;
)=3x;
![]() .
.![]()
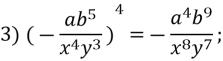
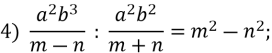
![]() =
=![]()
Варіант ІІ
Знайдіть помилки у розв’язанні прикладів та наведіть правильні розв’язання:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]()
![]()
Дії з раціональними
дробам
Як ми навчилися користуватися алгоритмами
Варіант І
Виконайте дії, заповнюючи пропуски:
![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() .
.
Варіант ІІ
Виконайте дії, заповнюючи пропуски:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() .
.
![]()
Дії з раціональними
дробами
Ми свідомо застосовуємо набуті знання
Варіант І
Виконайте дії та з наданих відповідей виберіть правильну:
1)![]()
Відповіді: а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г) інша відповідь.
; г) інша відповідь.
Додаткове завдання
2)* 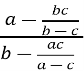
Відповіді: а) ![]() ; б)
; б)![]() ;
;
в) 1; г) інша відповідь.
Варіант ІІ
Виконайте дії та з наданих відповідей виберіть правильну:
1)![]()
Відповіді: а) ![]() ; б)
; б) ![]() ;
;
в)![]() г)інша відповідь
г)інша відповідь
Додаткове завдання
2)* 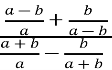
Відповіді: а) ![]() ; б)
; б)![]() ;
;
в) 1; г) інша відповідь.
![]()
Дії з раціональними
дробами
Навчаємось виконувати перетворення коренів за тотожностями
Тотожності
1)![]() ,
, ![]()
2)![]() ,
, ![]()
3)![]() натуральне число.
натуральне число.
ПРИКЛАДИ
Знайдіть значення виразу:
1)![]()
2)![]()
3)![]() =
=![]()
4)![]() =
=![]() ;
;
5)![]() =36.
=36.
![]() Варіант І Варіант ІІ
Варіант І Варіант ІІ
Знайдіть значення виразу: Знайдіть значення виразу:
1)![]()
2)![]() ; 2)
; 2)![]() ;
;
3)![]() ; 3)
; 3)![]() ;
;
4)![]() 4)
4)![]() ;
;
5)![]() ; 5)
; 5)![]()
6)![]() . 6)
. 6)![]() .
.
![]()
Квадратні корені
Навчаємось виконувати перетворення
коренів за тотожностями
Тотожності
1.![]() =
=![]() .
.
2.![]()
3.![]() =
=![]() натуральне число
натуральне число
4.![]()
5.![]()
![]() Варіант І Варіант ІІ
Варіант І Варіант ІІ
1) Спростіть вираз ![]() 1) Спростіть вираз
1) Спростіть вираз ![]()
2) Винесіть множник за знак кореня 2) Винесіть множник за знак кореня
![]() , якщо х
, якщо х![]()
![]() , якщо <
, якщо <![]()
3) Внесіть множник під знак кореня 3) Внесіть множник під знак кореня
![]() , якщо а
, якщо а![]()
![]() якщо х
якщо х![]()
4) Спростіть вираз 4) Спростіть вираз
(![]() (
(![]()
5) Позбавтесь ірраціональності 5) Позбавтесь ірраціональності
у знаменнику дробу у знаменнику дробу
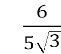
![]()
![]()
Квадратні корені
Як ми навчилися виконувати тотожності перетворення
виразів із коренями
Варіант І
Знайдіть помилки у розв’язанні вправ та наведіть правильні розв’язання.
1. Спростіть вираз:
1) ![]() , якщо х
, якщо х![]() .
. ![]() .
.
2) 3![]()
2. Порівняйте вирази 2![]()
3. Скоротіть дріб: ![]()
4. Розв’яжіть рівняння ![]() x+2=7; x=5.
x+2=7; x=5.
Варіант ІІ
Знайдіть помилки у розв’язанні вправ та наведіть правильні розв’язання.
1. Спростіть вираз:
1) ![]() , якщо b
, якщо b![]() .
. ![]() .
.
2) 5![]()
2. Порівняйте вирази 7![]()
3. Скоротіть дріб: ![]()
4. Розв’яжіть рівняння ![]() x - 5=3; x=8.
x - 5=3; x=8.
![]()
Квадратні корені
Як ми навчилися виконувати тотожні перетворення виразів із коренями
Варіант І
Виконайте вправи, заповнюючи пропуски.
1)![]() -
-![]() +
+![]()
2)![]()
2.Розкладіть на множники:![]()
3.Порівняйте:3![]() * 2
* 2![]() .
.
4.Спростіть вираз:![]()
![]() =
=![]()
Варіант ІІ
Виконайте вправи, заповнюючи пропуски.
1.Обчисліть:
![]() +
+![]() +
+![]() -
-![]() =2
=2![]() +4
+4![]() =*
=*
2)![]() =9.
=9.
2.Розкладіть на множники: 11-![]() =(
=(![]() -m)(
-m)(![]() +m).
+m).
3.Порівняйте: 10![]() .
.
4.Спростіть вираз:![]() ,якщо a
,якщо a![]()
![]() =
=![]()
![]()
Квадратні корені
Ми свідомо застосовуємо набуті знання
Варіант І
Виконайте вправи та з наданих відповідей виберіть правильну.
1.Спростіть вираз:
1) 5![]()
Відповіді: a) 5![]() , б)-5
, б)-5![]() , в) 5
, в) 5![]() , г) інша відповідь.
, г) інша відповідь.
2) ![]()
Відповіді: а)-1, б) 7-2![]() , в) 1-2
, в) 1-2![]() , г)інша відповідь.
, г)інша відповідь.
3) (1+![]() -
-![]() )(1+
)(1+![]() +
+![]() ).
).
Відповіді: а) 2![]() , б)0, в)16+2
, б)0, в)16+2![]() , г)інша відповідь.
, г)інша відповідь.
2.Розв’жіть рівняння:![]()
Відповіді: а) 13, б) 12, в) 3, г) інша відповідь.
3.Звільніться від ірраціональності в знаменнику дробу.![]()
Відповіді: а) ![]() . б)
. б) ![]() . в)
. в) ![]()
Варіант ІІ
Виконайте вправи та з наданих відповідей виберіть правильну.
1.Спростіть вираз.
1) -5а![]()
Відповіді: а) -5а![]() , б)5а
, б)5а![]() , в)-5а
, в)-5а![]() , г) інша відповідь.
, г) інша відповідь.
2)![]()
Відповіді: а) 1, б) -1, в) 2![]() -5, г) інша відповідь.
-5, г) інша відповідь.
3) (1+![]() )(1+
)(1+![]() +
+![]() , б)2
, б)2![]()
2.Розв’яжіть рівняння: ![]() =7.
=7.
Відповіді: а) 4, б) 25, в) 24, г) інша відповідь.
3.Звільніться від ірраціональності в знаменнику дробу: ![]()
Відповіді: а)-![]() -
-![]() , б)
, б) ![]() +
+![]() , в)
, в)![]() , г) інша відповідь.
, г) інша відповідь.
![]()
Квадратні корені
Навчаємося розв’язувати неповні квадратні
рівняння за схемою.
 Схема
Схема
![]()



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


 Корінь рівняння: Корені рівняння: Корені рівняння:
Корінь рівняння: Корені рівняння: Корені рівняння:
![]()
![]() x=0
x=0 ![]() = -
= -![]()
Якщо -![]()



![]() Приклад Приклад
Приклад Приклад ![]()
3![]()
х=0 х(4х-7)=0 -4![]()
![]() =4
=4
![]()
![]() Варіант І Варіант ІІ
Варіант І Варіант ІІ
Розв’яжіть рівняння: Розв’яжіть рівняння:
1) 7![]()
2)1,3![]()
3)![]()
Додаткове завдання: Додаткове завдання:
4) 5(![]()
![]()
Квадратні рівняння
Навчаємося розв’язувати повні квадратні
рівняння за алгоритмом
Алгоритм
![]()
1. Випишіть коефіцієнти а, b, c.
2. Знайдіть дискримінант за формулою D=![]()
3. Порівняйте значення дискримінанта з нулем та зробіть висновок про кількість коренів рівняння:
якщо D>0 – рівняння має два різні корені;
якщо D=0 – рівняння має два рівні корені;
якщо D![]() 0 – рівняння не має коренів.
0 – рівняння не має коренів.
4. Знайдіть корені рівняння за формулами: ![]() .
.
ПРИКЛАДИ
Розв’яжіть рівняння: ![]()
1. a=3, b=-5, c=2.
2. D=52-4 ![]() 3
3 ![]() 2=25-24=1.
2=25-24=1.
3. D>0, отже рівняння має два різні корені.
4. ![]() ;
; ![]() ;
;
Відповідь: ![]() .
.
![]()
Варіант І Варіант ІІ
1. Знайдіть дискримінант 1. Знайдіть дискримінант
рівняння ![]() рівняння
рівняння ![]()
Скільки коренів має рівняння? Скільки коренів має рівняння?
2.Розв’яжіть рівняння: 2. Розв’яжіть рівняння:
1) ![]() 1)
1) ![]()
2) ![]() 2)
2) ![]()
![]()
Квадратні рівняння
Навчаємося розв’язувати зведені квадратні
рівняння за теоремою Вієта
ТЕОРЕМА ВІЄТА
1. Для коренів х1 і х2 зведеного квадратного рівняння ![]() виконуються такі рівності: х1 +х2=-р і х1
виконуються такі рівності: х1 +х2=-р і х1 ![]() х2=
х2=![]() .
.
2. Якщо сума чисел m i n дорівнює (-р), а їхній добуток дорівнює ![]() , то числа m i n є коренями зведеного рівняння
, то числа m i n є коренями зведеного рівняння ![]()
ПРИКЛАДИ
1. У зведеному квадратному рівняння ![]() дискримінант
дискримінант
D=![]()
D>0; рівняння має два різні корені. За теоремою Вієта:
х1 +х2=16 і х1 ![]() х2=28
х2=28
2.Числа (-3) і 15 є коренями зведеного квадратного рівняння![]() .
.
Тому р=-(-3+15)=-12; ![]() =(-3)
=(-3)![]() 15=-45. Отже, рівняння має вигляд:
15=-45. Отже, рівняння має вигляд:
![]()
![]() Варіант І Варіант ІІ
Варіант І Варіант ІІ
1. Знайдіть суму і добуток коренів 1.Знайдіть суму і добуток коренів рівняння ![]() рівняння
рівняння ![]()
2. Визначте знаки коренів рівняння 2. Визначте знаки коренів рівняння
![]()
![]()
3. Запишіть квадратне рівняння, 3. Запишіть квадратне рівняння,
корені якого дорівнюють – 0,4 і 2,5 корені якого дорівнюють ![]() і 0,6
і 0,6
4. Один з коренів рівняння 4. Один з коренів рівняння
![]() дорівнює 9.
дорівнює 9. ![]() дорівнює 7.
дорівнює 7.
Знайдіть другий корінь. Знайдіть другий корінь.
![]()
Квадратні рівняння
Як ми навчилися розв’язувати квадратні рівняння
Варіант І
Знайдіть помилки в розв’язані вправ та наведіть правильні розв’язання.
1. Розв’яжіть рівняння:
1) 10х-5![]() =0 5х(5-х)=0 х=0 або х=-5;
=0 5х(5-х)=0 х=0 або х=-5;
2) 2![]() -7х-4=0 D=49+32=81
-7х-4=0 D=49+32=81 ![]() ;
; ![]()
3) ![]()
![]()
![]()
![]()
![]()
![]()
2. Запишіть квадратне рівняння, корені якого дорівнюють
![]()
![]()
![]()
![]()
Варіант ІІ
Знайдіть помилки в розв’язані вправ та наведіть правильні розв’язання.
1. Розв’яжіть рівняння:
1) 7![]() =0 7х(х-9)=0 х=0 або х=-9;
=0 7х(х-9)=0 х=0 або х=-9;
2) 3![]() -х-2=0 D=1+24=25
-х-2=0 D=1+24=25![]() ;
; ![]()
3) ![]()
![]()
![]()
![]()
![]()
![]()
![]() 2. Запишіть квадратне рівняння, корені якого дорівнюють
2. Запишіть квадратне рівняння, корені якого дорівнюють
![]()
![]()
![]()
![]()
Квадратні рівняння
Як ми навчилися розв’язувати квадратні рівняння
Варіант І
Розв’яжіть рівняння, заповнюючи пропуски:
1)![]()
D=36 – 4 ![]()
![]()
![]()
![]() ;
;
![]()
2)![]()
![]()
![]()
![]()
![]()
Відповідь: ![]()
Варіант ІІ
Розв’яжіть рівняння, заповнюючи пропуски:
1)![]()
D=225 – 4 ![]()
![]()
![]()
![]() ;
;
![]()
2)![]()
![]()
![]()
![]()
![]()
![]() Відповідь:
Відповідь: ![]()
Квадратні рівняння
Ми свідомо застосовуємо набуті знання
Варіант І
Розв’яжіть вправи та виберіть із наведених відповідей правильну
1. За яких значень змінної х числові значення виразів
![]()
Відповіді: а) ![]() і
і ![]() ; б) -1,4; в)
; б) -1,4; в) ![]() і
і ![]() г) інша відповідь.
г) інша відповідь.
2. Розв’яжіть рівняння ![]()
Відповіді: а) 2,5; б) -2,5; в) ![]() ; г) інша відповідь.
; г) інша відповідь.
3. Запишіть рівняння, корені якого протилежні кореням рівняння
![]()
Відповіді: а) ![]() ; б)
; б) ![]()
в) ![]() г) інша відповідь.
г) інша відповідь.
Варіант ІІ
Розв’яжіть вправи та виберіть із наведених відповідей правильну
1. За яких значень змінної х числові значення виразів
![]()
Відповіді: а)![]() ; б)
; б) ![]() ; в)
; в) ![]() г) інша відповідь.
г) інша відповідь.
2. Розв’яжіть рівняння ![]()
Відповіді: а) 2; б) ![]() ; в)-2; г) інша відповідь.
; в)-2; г) інша відповідь.
3. Запишіть рівняння, корені якого протилежні кореням рівняння
![]()
Відповіді: а) ![]() ; б)
; б) ![]()
в) ![]() г) інша відповідь.
г) інша відповідь.
![]()
Квадратні рівняння
 Навчаємось розв’язувати задачі за допомогою таблиці
Навчаємось розв’язувати задачі за допомогою таблиці
Варіант І
Розв’яжіть задачу, користуючись таблицею.
Знаменник звичайного дробу більший за його чисельник на 3. Якщо до чисельника цього дробу додати 7, а до знаменника 5, то дріб збільшиться на
![]() цей дріб.
цей дріб.
Заповніть порожні клітинки таблиці, складіть рівняння та знайдіть його корені.
|
Ситуація |
Запис дробу і його компонентів через невідоме |
||
|
Чисельник |
Знаменник |
Дріб |
|
|
Було (за умовою) |
х |
х+3 |
|
|
Стало (після перетворення) |
|
|
|
Відповідь:![]()

Варіант ІІ
Розв’яжіть задачу, користуючись таблицею.
Чисельник нескоротного звичайного дробу на 5 менший за знаменник. Якщо чисельник цього дробу зменшити на 2, а знаменник збільшити на 16, то дріб зменшиться на ![]() Знайдіть цей дріб.
Знайдіть цей дріб.
Заповніть порожні клітинки таблиці, складіть рівняння та знайдіть його корені.
|
Ситуація |
Запис дробу і його компонентів через невідоме |
||
|
Чисельник |
Знаменник |
Дріб |
|
|
Було (за умовою) |
х-5 |
х |
|
|
Стало (після перетворення) |
|
|
|
![]() Відповідь:
Відповідь:![]()
Текстові задачі
Навчаємось розв’язувати задачі за запропонованим алгоритмом
Варіант І
Розв’яжіть задачу, користуючись алгоритмом:
Моторний човен пройшов 45 км за течією річки і 22 км проти течії. Знайдіть власну швидкість човна, якщо на шлях за течією річки човен витратив на 1 год більше, ніж на шлях проти течії. Швидкість течії – 2км/год.
Алгоритм
1. Позначте власну швидкість човна х км/год (х>2).
2. Виразіть швидкість човна за течією річки, якщо швидкість човна х км/год, а швидкість течії річки 2 км/год.
3. Виразіть час, що човен витратив на шлях за течією, за формулою t=![]() .
.
4. Виразіть швидкість човна проти течії річки.
5. Виразіть час, який човен витратив на шлях проти течії річки.
6. Запишіть різницю між часом, який човен витратив на шлях проти течії і за течією.
7. Складіть рівняння, якщо відомо, що ця різниця дорівнює 1 год.
8. Розв’яжіть складене рівняння.
Відповідь: 13 км/год; 10 км/год.
Варіант ІІ
Розв’яжіть задачу, користуючись алгоритмом:
Туристи проплили на човні 15 к озером і 6 км проти течії річки за 5 год. Яка швидкість човна, якщо швидкість течії річки 2 км/год.
Алгоритм
1. Позначте швидкість човна х км/год (х>2).
2. Виразіть час, який туристи витратили на шлях озером, за формулою t=![]() .
.
3. Виразіть швидкість човна проти течії річки, якщо власна швидкість човна х км/год, а швидкість течії річки 2 км/год.
4. Виразіть час, який човен витратив на шлях проти течії річки.
5. Виразіть час, який човен рухався озером і проти течії річки разом.
6. Складіть рівняння, якщо за умовою цей час дорівнює 5 год.
7. Розв’яжіть складене рівняння.
Відповідь: 5 км/год.
![]()
Текстові задачі
Навчаємося знаходити область визначення
функції за зразком
Варіант І
Зразок. Знайдіть область визначення функції ![]() .
.
Розв’язання
Функції ![]() має зміст, якщо знаменник дробу не дорівнює 0.
має зміст, якщо знаменник дробу не дорівнює 0.
Отже, 2-3х![]() ; х
; х![]() .
.
Відповідь: всі значення змінної х, крім ![]() .
.
Знайдіть область визначення функції:
1) ![]() ;
;
2) ![]() ;
;
3)* ![]()
Варіант ІІ
Зразок. Знайдіть область визначення функції ![]() .
.
Розв’язання
Функції ![]() має зміст, якщо знаменник дробу не дорівнює 0.
має зміст, якщо знаменник дробу не дорівнює 0.
Отже, 5х-1![]() ; х
; х![]() .
.
Відповідь: всі значення змінної х, крім ![]() .
.
Знайдіть область визначення функції:
1) ![]() ;
;
2) ![]() ;
;
3)* ![]() .
.
![]()
Функції
Навчаємося досліджувати
 лінійні функції
лінійні функції
Варіант І
1. Побудуйте графік функції у=-2х+3, заповнивши таблицю:
|
х |
0 |
|
|
у |
|
0 |
2. Укажіть область визначення функції у=-2х+3.
3. За яких значень змінної х значення функції у=-2х+3 додатні?
4. Заповніть таблицю для функції у=0,5х+3.
|
х |
-4 |
-1 |
4 |
|
|
|
|
у |
|
|
|
-2 |
-0,5 |
6 |
5. Визначте, яка з точок – А(21;1) чи В(3;-6) – належить графіку функції ![]() , заповнюючи пропуски:
, заповнюючи пропуски:
А(21;1): ![]() ; В(3;-6):
; В(3;-6): ![]() Відповідь:
Відповідь:![]() .
.
6. У яких точках графік функції ![]() перетинає вісь Ох і вісь Оу?
перетинає вісь Ох і вісь Оу?

Варіант ІІ
1. Побудуйте графік функції у=2х-3, заповнивши таблицю:
|
х |
0 |
|
|
у |
|
0 |
2. Укажіть область визначення функції у=2х-3.
3. За яких значень змінної х значення функції у=2х-3 від’ємні?
4. Заповніть таблицю для функції у=-0,2х+4.
|
х |
-5 |
-1 |
5 |
|
|
|
|
у |
|
|
|
-4 |
1 |
4 |
5. Визначте, яка з точок – А(-3;1) чи В(3;2) – належить графіку функції ![]() , заповнюючи пропуски:
, заповнюючи пропуски:
А(-3;1): ![]() ; В(3;2):
; В(3;2): ![]() Відповідь:
Відповідь:![]() .
.
6. У яких точках графік функції ![]() перетинає вісь Ох і вісь Оу?
перетинає вісь Ох і вісь Оу?
![]()
Функції
 Навчаємося досліджувати функції виду
Навчаємося досліджувати функції виду ![]()
Варіант І
1. Побудуйте графік функції ![]() , заповнивши таблицю.
, заповнивши таблицю.
|
х |
-4 |
-2 |
-1 |
1 |
2 |
4 |
|
у |
|
|
|
|
|
|
2. Укажіть область визначення функції ![]() .
.
3. За яких значень змінної х значення функції ![]() додатні?
додатні?
4. Графік функції ![]() проходить через точку М(3;-3).
проходить через точку М(3;-3).
Чи проходить графік через точку С(-3;3)?
5. У яких чвертях розташовано графік функції ![]() ?
?

Варіант ІІ
1. Побудуйте графік функції ![]() , заповнивши таблицю.
, заповнивши таблицю.
|
х |
-6 |
-3 |
-2 |
-1 |
1 |
2 |
3 |
4 |
6 |
|
у |
|
|
|
|
|
|
|
|
|
2. Укажіть область визначення функції ![]() .
.
3. За яких значень змінної х значення функції ![]() додатні?
додатні?
4. Графік функції ![]() проходить через точку М(-2;4).
проходить через точку М(-2;4).
Чи проходить графік через точку С(-8;-1)?
5. У яких чвертях розташовано графік функції ![]() ?
?
![]()
Функції
Як ми навчилися розпізнавати функції
Варіант І
1. Яка з функцій: а)![]() ; б)
; б) ![]() ; в)
; в) ![]() – є оберненою пропорційністю?
– є оберненою пропорційністю?
2. На якому рисунку зображено графік прямої пропорційності?
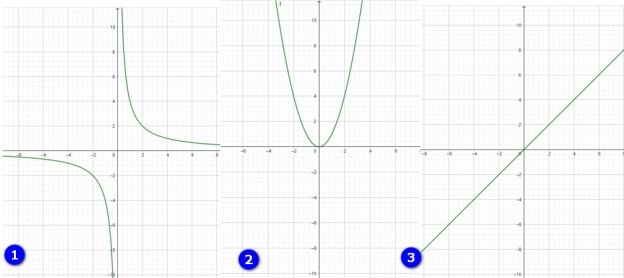
Варіант ІІ
1. Яка з функцій: а)![]() ; б)
; б) ![]() чи б)
чи б)![]() – є лінійною?
– є лінійною?
2 На якому рисунку зображено графік оберненої пропорційності?

![]()
Функції
Як ми навчилися досліджувати функції
![]()
 Варіант І
Варіант І
1. Побудуйте графік функції ![]() , заповнивши таблицю.
, заповнивши таблицю.
|
х |
0 |
1 |
2 |
-1 |
-2 |
|
у |
|
|
|
|
|
2. За яких значень змінної х значення функції ![]() додатні?
додатні?
3. За яких значень змінної х функція ![]() спадає?
спадає?
4. Укажіть область визначення функції ![]() .
.
5. Яких значень набуває змінна у для функції ![]() ?
?
6. Чи проходить графік функції ![]() через точки А(4;-2) і В(9;3)?
через точки А(4;-2) і В(9;3)?

Варіант ІІ
1. Побудуйте графік функції ![]() , заповнивши таблицю.
, заповнивши таблицю.
|
х |
0 |
1 |
4 |
9 |
|
у |
|
|
|
|
2. Чи існують значення змінної х, для яких значення функції ![]() від’ємні? Чому?
від’ємні? Чому?
3. Чи можна вказати значення змінної х, при яких функція ![]() спадає?
спадає?
4. Чи проходить графік функції ![]() через точки М(-6; -36) і К(-6;36)?
через точки М(-6; -36) і К(-6;36)?
5. Укажіть область визначення функції ![]() .
.
6. Яких значень набуває змінна у для функції ![]() ?
?
![]()
Функції
![]()


про публікацію авторської розробки
Додати розробку
