Початковий і середній рівні (6 балів)

Позначте одну правильну, на вашу думку, відповідь.

1. Розв’яжіть рівняння .

                А 14                             Б –2                             В 2                               Г  

Розв’язання

       | Перенесіть у ліву частину рівняння доданок, який містить невідоме з протилежним знаком

2. Розв’яжіть рівняння

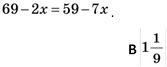                А –2                              Б 2                                                                 Г  

Розв’язання

        | Перенесіть у ліву частину рівняння всі доданки, який містять невідоме з протилежним знаком, а в праву — всі доданки, що не містять невідомого

3. Розв’яжіть рівняння .

                А –2                              Б 7                              В 2; –7                         Г –2; 7

Розв’язання

          | Добуток дорівнює нулю коли хоча б один із множників дорівнює нулю

  або   

Відповідь: Г

4. Складіть рівняння до задачі.

У магазин завезли 232 кг фруктів і продали за два дні. Другого дня було продано в 3 рази менше фруктів, ніж першого. Скільки фруктів продали першого та другого дня окремо?

                 А                   Б              В           Г  

Розв’язання

І дня — ?, в 3 рази більше, ніж 

 232 кг

ІІ дня — ?, х кг

Нехай другого дня було продано х кг фруктів, тоді першого дня продали 3х кг фруктів. За два дні продали 232 кг. Складемо рівняння:

Відповідь: В

5. Складіть рівняння до задачі.

Периметр прямокутника дорівнює 14,8 дм. Довжина однієї з його сторін на 4,2 дм менша за довжину іншої. Знайдіть сторони прямокутника.

Нехай довжина однієї сторони х дм, тоді другої сторони — (х – 4,2) дм. Периметр прямокутника дорівнює (Р = 2(а + b)) 14,8 дм. Отримали рівняння:

Відповідь: В

6. Складіть рівняння до задачі.

Легковий автомобіль за 4 год пройшов шлях, який вантажівка долає за 6 год. Знайдіть швидкості автомобілів, якщо швидкість вантажівки на 20 км/год менша за швидкість легкового автомобіля.

                    А               Б             В         Г  

Розв’язання

Нехай швидкість вантажівки х км/ год, тоді швидкість легкового автомобіля — (х + 20) км/год. Відстань, яку долає легковий автомобіль за 4 години дорівнює 4(х + 20)  км, а вантажівка за 6 год — 6х км . За умовою задачі, відстані які вони долають однакові. Складемо рівняння:

Відповідь: В

Достатній рівень (3 бали)

7. Розв’яжіть задачу.

Від пристані вниз по річці відправили пліт, який рухався зі швидкістю 4 км/год. Через 3 год слідом за ним відійшов човен, власна швидкість якого 9 км/год. На якій відстані від пристані човен наздожене пліт?

Розв’язання

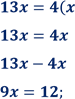
Нехай човен рухався х год, тоді пліт – (х + 3) год. Швидкість човна за течією — 13 км/год, тоді човен долає відстань 13х км, а пліт — 4(х + 3) км. За умовою задачі човен наздоганяє пліт. Отже відстані які вони долають однакові. Складемо рівняння:

(год) рухався 

(км) від пристані човен наздожене пліт

Відповідь: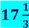км

8. Розв’яжіть рівняння .

Розв’язання

                   | Застосуємо основну властивість пропорції

 Відповідь: 2

Високий рівень (3 бали)

9. Розв’яжіть рівняння .

або

Відповідь: