Аналізуємо практичне завдання

Початковий і середній рівні (6 балів)

Позначте одну правильну, на вашу думку, відповідь.

1. Розв’яжіть рівняння .

А 22                             Б –2                             В 2                                   Г  

Розв’язання:

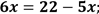       |Перенесіть у ліву частину рівняння доданки, які містять невідоме з протилежним знаком (с. 316)

 

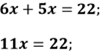
Відповідь: В

А 8                                      Б –8                                         В 1,6                                         Г –1,6

Розв’язання:

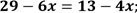   |Перенесіть у ліву частину рівняння доданки, які містять невідоме з протилежним знаком, а в праву — всі доданки, що не містять невідомого з протилежним знаком

 

 

Відповідь: A

А 0                               Б 2                                В Немає розв’язків     Г 2; 0

Розв’язання:

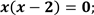      | Якщо добуток дорівнює нулю, то хоча б один із множників дорівнює нулю (с. 287)

 

Відповідь: Г

4.  Складіть рівняння до задачі.

За два дні було продано 245 кг овочів. Першого дня продано в 4 рази більше, ніж другого. Скільки овочів було продано першого та другого дня окремо?

А                         Б                 В                   Г  

Розв’язання:

І дня — ?, в 4 рази більше, ніж 

ІІ дня — ?, х кг

 Нехай другого дня було продано х кг овочів, тоді першого дня — 4х кг. За два дні було продано 245 кг. Отримали рівняння:  

Відповідь: Б

5.  Складіть рівняння до задачі.

Периметр прямокутника дорівнює 15,6 дм. Довжина однієї з його сторін на 2,8 дм більша від довжини іншої. Знайдіть сторони прямокутника.

А                Б           В              Г  

Розв’язання:

І сторона — ?, на 2,8 дм більша від  

ІІ сторона — ?, х дм

Нехай довжина другої сторони прямокутника дорівнює х дм, тоді довжина першої сторони прямокутника — (х + 2,8)дм. Периметр прямокутника дорівнює 15,6 дм (Р = 2a + 2b = 2(a + b)). Складемо рівняння:

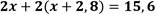;  | Заміна виразу ab + acна вираз a(b + c) називають винесення спільного множника  за дужки (с. 302)

 

Відповідь: Г

6. Складіть рівняння до задачі.

Пішохід пройшов за 45 хв таку саму відстань, яку велосипедист проїхав за 15 хв. Знайдіть швидкість кожного з них, якщо швидкість велосипедиста на 5 м/хв більша за швидкість пішохода.

А            Б           В           Г  

Розв’язання:

Нехай швидкість пішохода х м/хв, тоді швидкість велосипедиста — (х + 5) м/хв. Пішохід за 45 хв долає відстань 45х м, а велосипедист за 15 хв — 15(х + 5) м. В умові задачі маємо однакову відстань.

Складемо рівняння:  

Відповідь: B

Достатній рівень (3 бали)

7. Теплохід проходить за 15 год проти течії річки таку саму відстань, яку він подолає за 13 год за течією річки. Знайдіть швидкість течії річки, якщо власна швидкість теплохода 70 км/год.

Розв’язання:

 

Нехай швидкість течії річки дорівнює х км/год, тоді швидкість теплохода проти течії річки дорівнює (70 – х) км/год, а за течією річки — (70 + х) км/год. Відстань, яку долає теплохід за 15 год проти течії річки дорівнює 15(70 – х) км/год, а за 13 год за течією – 13(70 + х) км/год. З умови задачі маємо однакову відстань. Складемо рівняння:

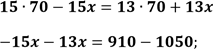
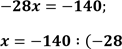
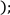
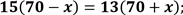   | Розкриємо дужки, застосовуючи розподільну властивість множення відносно віднімання та додавання

 (км/год) швидкість течії

Відповідь: 5 км/год

Розв’язання:

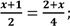    | Застосуємо основну властивість пропорції (с. 157)  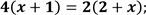   | Розкриємо дужки

 

      Відповідь: 0

Високий рівень (3 бали)

9. Розв’яжіть рівняння .

Розв’язання:

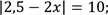    | Модуль – відстань від початку відліку до точка, яка зображує це число на координатній прямій

  

або

 

Відповідь: -3,75; 6,25