Аналіз міждисциплінарного зв'язку між математикою та іншими навчальними дисциплінами та математичні компетенції, якими повинен володіти учень для успішної реалізації своїх

Практична робота

      Аналіз міждисциплінарного зв'язку  між математикою та іншими навчальними дисциплінами та  математичні компетенції,  якими повинен володіти учень для успішної реалізації своїх професійних знань у майбутньому.

Зміст

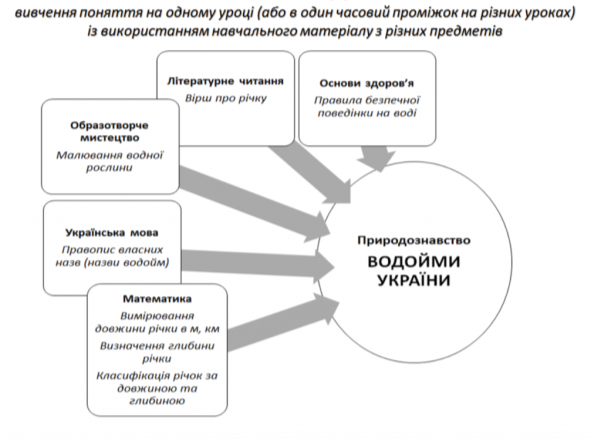
         На основі подібності змісту фундаментальних природничо-наукових, професійно-практичних дисциплін у підготовці  учнів, міждисциплінарні зв‘язки дозволяють побудувати цілісну систему навчання, в якій можна виділити: – основні елементи змісту підготовки; – взаємозв‘язки між навчальними дисциплінами, в т. ч. практик; – взаємозв‘язки між темами в самій дисципліні. За рахунок їх використання в організації освітнього процесу можна досягти збільшення науковості навчання, його доступності, що призведе до удосконалення процесу формування знань, умінь і навичок. При впровадженні міждисциплінарних зв‘язків у навчанні необхідно враховувати їх багаточисельність і в кожному конкретному випадку викладач вибирає форми і методи їх застосування.   В основі міждисциплінарної інтеграції лежить принцип міжпредметних зв‘язків, який виконує освітню, розвиваючу та виховну функції. Даний принцип сприяє формуванню системності знань, розвитку системного, самостійного мислення, пізнавальної активності  учнів, а також формує у них світоглядні переконання. 

      Одним з напрямків інтенсифікації й активізації навчального процесу, активізації навчально-пізнавальної діяльності  учнів є використання міжпредметних зв’язків математики з іншими навчальними дисциплінами. Міжпредметні зв’язки – це розвиток основних положень загальнонаукових теорій та законів, що вивчаються на заняттях зі споріднених дисциплін з метою засвоєння  учнями  цілісної теорії. Способи використання знань інших предметів можна визначити на основі ретельного вивчення навчальних програм, планів та матеріалів підручника.

       У навчанні математики міжпредметні зв’язки виконують методологічну, освітню, розвивальну, виховну, конструктивну функції.

• Методологічна функція полягає в тому, що тільки на базіміжпредметних зв’язків можливе формування у  учнів цілісного погляду на світ, на чому свого часу наголошував академік В.І. Вернадський.
• Навчальна функція полягає у формуванні  таких якостей набутих знань з математики, як системність, глибина, усвідомленість, гнучкість, що сприяють засвоєнню зв’язків між математичними та загальними поняттями.
• Розвивальна функція визначається роллю міжпредметних зв’язків в розвитку самостійного й творчого мислення  учнів, у формуванні їх пізнавальної активності, самостійності та інтересу до пізнання математики.
• Виховна функція полягає у сприянні міжпредметних зв’язків комплексного підходу до виховання молоді під час навчання математики.
• Конструктивна функція полягає в тому, що за допомогою міжпредметних зв’язків викладач удосконалює зміст навчального матеріалу, методи і форми навчання.

        Найбільш прозорими є міжпредметні зв’язки математики з фізикою, теоретичною механікою, спеціальними дисциплінами, при вивченні яких використовуються ряди, диференціальні рівняння тощо. Міжпредметність є сучасним принципом навчання, що впливає на відбір та структуру навчального матеріалу цілого ряду дисциплін, підсилює системність засвоєних знань, активізує навчання, орієнтує на застосування комплексних форм організації навчання, забезпечує єдність навчальновиховного процесу. Розвитку активності й самостійності  учнів при вивченні математики сприяє розв’язування задач міжпредметного змісту, прикладних, професійно спрямованих та дослідницьких задач. Можна сформулювати такі вимоги до складання цих задач: задача повинна бути правильно поданою викладачем, бути зрозумілою, бути посильною для  учнів, викликати інтерес завдяки зовні цікавого формулювання, незвичної постановки запитання або процесу розв’язування, а також розвивати життєвий досвід  учнів, показувати можливість використання набутих знань у деяких життєвих ситуаціях.

         Задачі міжпредметного змісту, професійно спрямовані, дослідницькі задачі виконують наступні функції:

  освітню (використання цих задач спрямовано на формування   системи знань, навичок і вмінь на різних етапах навчання математики),

 розвивальну (опрацювання таких задач розвиває вміння осмислювати отримані результати, робити відповідні узагальнення, порівняння, висновки),

 виховну (виховання майбутнього фахівця на заняттях з математики може здійснюватися завдяки означеним задачам),

 контролюючу (ці задачі є навчальними). Розв’язання задач міжпредметного змісту сприяє формуванню і розвитку базових, предметних, зокрема математичних, професійних і практичних компетентностей.

Пріклад

      Математичні компетенції, на  мій розсуд,  якими повинен  володіти учінь для успішної реалізації своїх професійних знань у майбутньому.

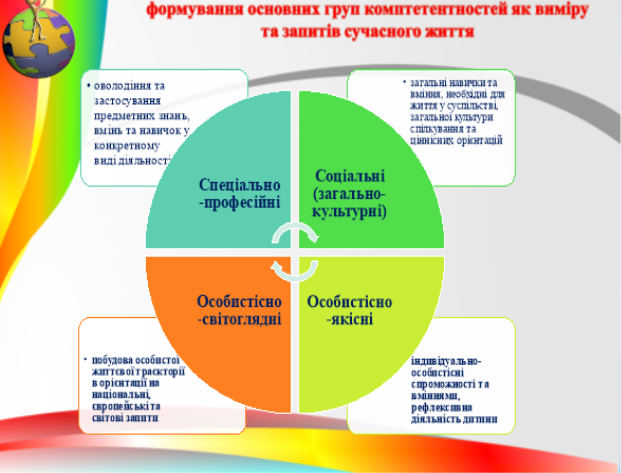
1. Спеціально-професійне.     Оволодіння та застосування предметних знань, вмінь та навичок у конкретному виді діяльності.
2. Соціальні (загально-культурні).  Загальні навички та вміння, необхідні для життя у суспільстві, загальної культури спілкування та ціннісних орієнтацій.
3. Особистісно-якісні.  Індивідуально-особистісні спроможності та вміння, рефлексивна діяльність дитини.
4. Особистісно-світоглядні. Побудова особистої життєвої траєкторії в орієнтації на національні, європейські та світові запити.