Курсова робота "ДИФЕРЕНЦІЙОВАНЕ НАВЧАННЯ ЯК ОДИН З МЕТОДІВ СТВОРЕННЯ СИТУАЦІЇ УСПІХУ"

 

 

 

 

 

 

 

ВИПУСКНА КВАЛІФІКАЦІЙНА РОБОТА

 

На тему:

 

« ДИФЕРЕНЦІЙОВАНЕ НАВЧАННЯ ЯК ОДИН З МЕТОДІВ СТВОРЕННЯ СИТУАЦІЇ УСПІХУ»

 

 

 

 

 

 

 

 

 

 

 

 

                                                          Демченко Оксани Георгіївни

(П.І.Б)

                                                                                        вчителя  математики, інформатики     

(посада слухача)

КЗ «Маріупольська загальноосвітня

                                                школа I-III  ступенів №18

                                                      Маріупольської міської ради

                                      Донецької області»

                                                                                місце роботи слухача

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗМІСТ

 

ВСТУП………………………………………………………………………...3

1. Сутність і шляхи реалізації принципів індивідуалізації і диференціації навчання……………………………………………………………………….3
2. Індивідуальний підхід - необхідна умова розвитку мислення учнів в процесі навчання математики………………………………………………..6
3. Реалізація індивідуального підходу до учнів при навчанні математики…………………………………………………………………...10
4. Технологія рівневої диференціації навчання математики………………..13
5. Реалізація розвиваючого навчання при навчанні математики (типи уроків)………………………………………………………………………...16

Висновок……………………………………………………………………..23

Доданок………………………………………………………………………24

Список використаної літератури…………………………………………...30

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Навчання учнів математиці це навчання їх математичній діяльності. Математична діяльність – формування та розвиток розумової діяльності визначеної структури. Загальноосвітня мета викладання математики вимагає від учителя: передати учням певну систему математичних знань, навичок; навчити усній і письмовій математичній мові; допомогти учням досягти обов’язкових результатів навчання, навчити застосовувати набуті знання для розв’язання найпростіших завдань життєвої практики та вивчення інших навчальних предметів; ознайомити з шляхами пізнання реальної дійсності, математичними методами; навчити користуватися математичними інструментами та приладами, а також умінню самостійно здобувати знання (робота з підручником, науково-популярною літературою).

Принцип доступності вимагає, щоб обсяг і зміст навчального матеріалу були під силу учням, відповідали рівню їх розумового розвитку та запасу знань, вмінь і навичок. Слід відмітити, що спрощений зміст навчання знижує його розвивальні і виховні можливості. Тому рекомендується (за Л.В. Занковим), щоб зміст завдань для учнів знаходився в зоні їх найближчого розвитку.

 

СУТНІСТЬ І ШЛЯХИ РЕАЛІЗАЦІЇ ПРИНЦИПІВ      ІНДИВІДУАЛІЗАЦІЇ І ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ

 

Під індивідуалізацією слід розуміти організацію процесу навчання на основі врахування індивідуальних особливостей учнів.

Під диференціацією слід розуміти організацію процесу навчання за декількома різними навчальними планами, програмами, завданнями в формі окремих груп, створених на основі врахування будь-яких узагальнених індивідуальних особливостей школярів.

Диференціація навчання є варіантом індивідуалізації, способом реалізації індивідуального підходу до учнів. Відмінність диференціації від індивідуалізації полягає в тому; що врахування індивідуальних особливостей учнів здійснюється в такій формі, де учні групуються на основі будь-яких особливостей для окремого навчання в умовах класу.

Суть принципу індивідуального підходу заключається в адаптації (пристосуванні) навчання до змісту і рівня знань, умінь та навичок кожного учня або до характерних для нього особливостей процесу засвоєння, або навіть до деяких стійких рис його особистості.

Основним засобом реалізації даного принципу є індивідуальні самостійні роботи, котрі виступають як дидактичний засіб організації і керівництва самостійною діяльністю учнів на всіх етапах навчання.

Під диференціацією розуміють таку систему навчання, при якій кожен учень одержує право і можливість приділяти переважну увагу тим напрямкам навчання, котрі у найбільшій мірі відповідають його схильностям. Види диференціації: рівнева і профільна.

Рівнева диференціація виражається у тому, що навчаючись в одному класі, за однією програмою та підручником, школярі можуть засвоювати матеріал на різних рівнях. Визначальним при цьому є рівень обов’язкової підготовки.

Профільна диференціація припускає навчання різних груп школярів за програмами, котрі відрізняються глибиною викладання матеріалу, обсягом відомостей і навіть номенклатурою питань, що вивчаються. Обидва види диференціації - рівнева та профільна - існують і взаємно доповнюють один одного на всіх ступенях шкільної математичної освіти, однак у різній питомій вазі.

У основній школі головним видом диференціації є рівнева. Профільне навчання математики у основній школі може існувати у рамках поглибленого вивчення математики, починаючи з 8 класу. На старшій ступені школи пріоритет віддається різноманітним формам профільного вивчення  предметів.

 

 

Вимоги до здійснення рівневої  диференціації:                     

• відкрите пред’явлення рівня обов’язкової підготовки повинно

         здійснюватися на всіх етапах навчання, учням повинні бути зрозумілі  

         і відомі наочні, повсякденні, так і підсумкові обов’язкові вимоги;

• рівень, на якому ведеться викладання, повинен бути вище обов’язкового рівня засвоєння матеріалу;
• всі учні повинні пройти через етап опорних знань, через етап роботи над обов’язковими результатами;
• послідовне просування за рівнями;
• облік індивідуального темпу досягнення обов’язкових результатів;
• відповідність змісту, контролю і оцінки прийнятому рівневому підходу;
• добровільний вибір засвоєння і звітності.

Виділеним і відкрите пред’явлення всім учасникам навчального процесу рівня обов’язкової підготовки є основою диференціації навчання.

Досягнення рівня обов’язкової підготовки є критерієм, підставою для організації диференційованої роботи у класі. Контроль повинен передбачати для всіх учнів перевірку обов’язкових результатів навчання і доповнюється перевіркою засвоєння матеріалу на більш високих рівнях.

Засвоєння матеріалу всіма учнями на обов’язковому рівні вимог програми називають базовим рівнем. Підвищення базового рівня спів відносно здібностям, бажаним і інтересам учнів називають підвищеним рівнем.

Вимоги до математичної підготовки сформульовані для кожного ступеня школи в програмі з математики і відображають собою цільові установки по відношенню до підсумкового результату навчання для кожного ступеня. Для кожного ступеня виділено два рівня оволодіння матеріалом:

- рівень обов’язкової підготовки (визначає той безумовний мінімум підготовки, який повинен бути осягнений кожним учнем із закінченням ступеня, і відповідає оцінці "4 – 6");

- підвищений рівень математичної підготовки, який повинна забезпечити школа для випускників, які мають оцінку "10 – 12".

Досягнення підвищеного рівня дає достатньо основу для одержання вищої освіти за спеціальностями, які пов’язані із застосуванням математики.

Диференціація навчального процесу математики реалізується через і дозування навчального матеріалу для учнів із врахуванням їх загального розвитку; намаганням кожного школяра розвивати свої власні здібності на ;основі відповідних умов, які є в школах-ліцеях, школах-гімназіях.

 

ІНДИВІДУАЛЬНИЙ ПІДХІД – НЕОБХІДНА УМОВА РОЗВІДКУ МИСЛЕННЯ УЧНІВ В ПРОЦЕСІ НАВЧАННЯ МАТЕМАТИКИ

 

Зміст принципу індивідуального підходу полягає в такій організації навчального процесу, при якому вибір методів, прийомів і темп навчанні враховує індивідуальні відмінності учнів, рівень їх здібності до навчання. Рушійними силами індивідуалізації є протиріччя між фронтально побудованим процесом пред’явлення нового матеріалу і індивідуальним характером його засвоєння. Цей принципів має давню історію. Ще К.Д.Ушинський говорив, що ділити клас на дві групи, одна з яких сильніша другої, не тільки не шкода, але навіть корисно, якщо наставник вміє, займаючись з однієї групою сам, другій дати користю самостійну вправу. В педагогіці питання індивідуалізації розроблялись П.П.Блонським, О.М. Гельмонтом. Але особливе піднесення уваги до проблеми індивідуалізації навчання відбувається наприкінці 60-х, в 70-х   років   дидактичних   роботах     Ю.К. Бабанського,   Е.С. Рабунського,

О.О. Бударного,   І.Е. Унт,   І.М. Чередова,       І.С. Якіманської,      психологів

Н.О. Менчинсьюї, З.І. Калмикової і багатьох інших. В рамках розвиваючого індивідуального підходу відбувається глибоке вивчення індивідуальних психологічних особливостей учнів, перерозподіл уваги від слабких учнів до різних груп школярів; робиться спроба побудувати навчальний процес з урахуванням індивідуально-психологічних особливостей сприймання і мислені учнів на основі теорії діяльності. Е.С.Рабунський означає індивідуальний підхід як дійову увагу до кожного учня, його творчої індивідуальності в умовах класно урочної системи навчання, припускає розумне сполучення фронтальних, групових і індивідуальних занять для підвищення якості навчання і розвитку кожного школяра.

Індивідуальний підхід припускає вивчення одних і тих же питань програми на різних рівнях, в залежності від підготовленості учнів, їх інтересів здібностей та інших критеріїв так, щоб кожний учень був зайнятий на уроці, щоб не допускати прогалин в знаннях школярів. “Усі діти здатні до навчання, кожний нормальний психологічно здоровий школяр здатний одержати середню освіту, більш чи менш успішно оволодіти навчальним матеріалом в межах шкільних програм, і учитель повинен добиватись цього стосовно всіх учнів”. Але звідси зовсім не випливає, що всіх учнів можна однаково легко навчити. Навчальний процес повинен не просто пристосовуватись, підбудовуватись під власний рівень знань і умінь учнів, змінюючи зміст і методи, а орієнтуватись на досягнення максимально важливих результатів кожним учнем і, що не менш важливе, на розвиток мислення, пізнавальних можливостей, інтересів.

Диференційний підхід в навчанні – це засіб реалізації індивідуального підходу. Орієнтація навчання на середнього учня себе не виправдовує, оскільки при цьому по різному використовується потенціал слабких і сильних учнів. Останній надається сам собі, чим пояснюється втрата інтересу до навчання.

В ряді робіт відмічається, що організація індивідуального підходу до учнів в умовах звичайного уроку є слабким місцем в організації навчання. Дуже часто індивідуальний підхід розуміється тільки як доробка матеріалу, ліквідація прогалин після уроків і під час його проведення. В той же час глибоке виникнення учителем в розумовий процес засвоєння, розуміння ним психологічних особливостей матеріалу, що вивчається, дозволяє попереджувати труднощі і нівелювати рівень засвоєння різними учнями. Досвід показує, що кваліфікована організація диференційного підходу в навчанні вимагає великих часових витрат для підготовки до уроку, глибоких педагогічних, психологічних знань і важка для одного учителя. Найбільш сприятлива можливість організації індивідуального підходу з’являється при централізованому матеріальному забезпеченні навчального процесу спеціальними методичними матеріалами.

Розглянемо різні точки зору на організацію індивідуального підходу; які є в психолого-педагогічній літературі. В основу типології учнів, яка необхідна для організації диференційного підходу, в ряді робіт покладено критерій навчання.   Це   поняття    розроблено    З.І. Калмиковою,     Н.О. Менчинською,

Д.Н. Богоявленським. Навчання – це особливість розумової діяльності, “…під навчанням ми розуміємо складну динамічну систему інтелектуальних властивостей особи, що формують якості розуму, від яких залежить продуктивність учбової діяльності ”.

І.Е. Унт пропонує проводити типологію учнів за семи критеріями: навчаємість, навченість, вміння самостійно працювати, вміння читати зрозумінням і з потрібною швидкістю, спеціальні здібності, пізнавальний інтерес, відношення до праці. Е.С. Рабунським в якості критеріїв типології виділені наступні: рівень успішності, рівень пізнавальної самостійності, під яким автор розуміє і здібності, і організованість в навчанні; інтереси. Сполучення трьох рівней – високого, середнього і низького – кожного з виділених критеріїв дозволяє детально кваліфікувати склад класу і передбачати міри допомоги окремим школярам.

Але в практичній роботі учителю на уроці дуже важко орієнтуватись на різні фактори, практично він не може організувати роботу одночасно  більш ніж з 2-3 групами. Отже, щоб була можливість управлінь діяльністю в цих групах, клас не може бути розбитий більше ніж на 2-3 групи. Для такої розбивки потрібен один, але найбільш важливий критерій. Таким критерієм може бути рівень розвитку мислення. В багатьох методичних роботах питання індивідуалізації розв’язується в плані попередження помилок і засвоєння змісту. Цього недостатньо. Необхідно організовувати індивідуальний підхід так, щоб він не просто забезпечував засвоєння знань, але й сприяв розвитку учнів. Ця думка точно сформульована О.О. Кирсановим: “... одна з принципових вимог до навчальної діяльності — не пристосування навчання до рівня підготовленості учня шляхом зниження об’єктив труднощів, а систематичне, послідовне, цілеспрямоване розширення і потенціальних можливостей до об’єктивних вимог ”.

У школярів по різному розвинені розумові операції, сформовані прийоми розумової діяльності, у кожного учня своя “ зона найбільшого розвитку ”. Крім того, як підкреслює 3.І. Калмикова, основною внутрішньою причиною відставання в навчанні у більшості невстигаючих школярів є більш низький, ніж у їх одноліток рівень розвитку мислення. За даними      Ю.К. Бабанського, найбільш висока кореляція успішності навчання долається з компонентами інтелектуального розвитку. 3 самостійністю мислення коефіцієнт кореляції дорівнює 0,89; з виділенням суттєвого – 0,8 гнучкістю – 0,85; з логічністю мови – 0,85; з критичністю – 0,84. Причому учні з затримкою в розумовому розвитку – найбільш складний тип встигаючих.

У дітей із зниженим навчанням немає патологічних змін в пам’яті пов’язаної з мисленням, але страждає логічна пам’ять. При відповідних  умовах слабкі учні концентрують увагу однаково з сильними. Але “… другим явищем, її не можна вважати першопричиною виникнення  труднощів, вона сама обумовлена тим, що учень через особливості свого мислення не втягується в активну навчальну роботу”.

Активність учнів також залежить від розвитку мислення. Рівень практичних дій і у сильних і у слабких школярів практично однаковий. Мотивація, відношення до учня  також залежить від того, як учень справляється з роботою, чи отримує він задоволення від неї  чи ні. Наведені міркування говорять про те, що з усіх критеріїв, що використовуються для організації індивідуального підходу до навчання учнів, рівень розвитку мислення – найважливіший. Аналіз методичної літератури показує, що проблема індивідуалізації навчання часто розв’язується без урахування мети розвитку мислення. Учитель з досвідом робить це інтуїтивно вірно, але початківець захоплюється зовнішньою стороною індивідуального підходу. Необхідно, щоб обидва могли свідомо їх реалізовувати.

 

 РЕАЛІЗАЦІЯ ІНДИВІДУАЛЬНОГО ПІДХОДУ ДО УЧНІВ ПРИ НАВЧАННІ МАТЕМАТИКИ

 

Група сильних учнів – неоднорідна група. В роботі В.А. Крутецького виділено три основні стадії розумової діяльності в процесі розв’язування будь-яких задач: отримання інформації про задачу, переробка інформації, збереження інформації.

  У зв’язку з цим виділяються три компоненти структури математичних здібностей: особливості отримання інформації про задачу, її перетворення і зберігання. Здається, що сильні учні, сприймаючи математичну задачу, виділяють її структуру, систематизують дані. В задачі вони звертають увагу не на конкретні чи числові значення, а на функціональні залежності, розрізняють суттєве і несуттєве для даної задачі. У процесі перетворення отриманої інформації учні з розвинутим мисленням проявляють здібності до узагальнення. Для сильних учнів характерні мислення згорнутими структурами, скороченими висновками, гнучкість розумових процесів здібність до швидкого і вільного переключення з прямого на обернений хід думки, цим школярам притаманна організована система пошуку підкорена певному плану. Проби сильних учнів – це завжди цілеспрямовані і систематизовані пошуки, спрямовані на перевірку зробленого. На стадії зберігання вони не запам’ятовують дані, але добре пам’ятають способи розв’язання.

Як ми можемо бачити, на всіх трьох ступенях розв’язання першу чергу виявляється добре розвинена розумова операція узагальнення (виділяються не числові дані, а функціональні залежності, запам’ятовуються не дані, а спосіб розв’язання і т.д.). Крім особливостей розумової діяльності, які були виділені В.А. Крутецьким, З.І. Калмикова відмічає і стійкість розуму, яка проявляється в орієнтації на сукупність ознак, не дивлячись на провокуючу дію випадкових ознак та усвідомленість власної розумової діяльності. Усвідомленість проявляється у можливості виразити слові або інших символах ціль, результат і спосіб розумової дія також в здібності виявити помилкові шляхи і їх причини.

Типологія, запропонована Рабунським, проводиться теоріями: рівень успішності, пізнавальна самостійність і інтерес. В цій типології нас наперед усього цікавлять учні з достатньо розвинутим другим критерієм. Рівні успішності і організованості, які є додатками пізнавальної самостійності, можуть бути при цьому різними. Автор виділяє дві групи учнів з високою пізнавальною самостійністю. Вони розрізняються за глибиною інтересу: в одних інтерес – глибокий І дійовий, в інших – вузько вибраний або потенціальний при недостатній організованості. Напрямки роботи учителя з такими учнями різні. В першому випадку – це задоволення високої витрати, в другому – перетворення потенціального інтересу в дійовий. Задоволення високої пізнавальної витрати можна здійснити через залучення до факультативних занять, до позакласної роботи, до систематизованого позакласного читання, надання взаємодопомоги учням у виконанні  завдань за бажанням школярів і т.д. Для другої групи учнів Рабунський пропонує раціонально організувати роботу на заняттях, виховувати в них елементарну організованість в домашній роботі. Тут важлива також залежність проблемності завдань з урахуванням позаучбових нахилів і розрахованих на довгу підготовку, читання додаткової літератури.

В методичній літературі для організації роботи з сильними учнями пропонуються також індивідуальні завдання на відшукання різних засобів розв’язування однієї і тієї ж задачі, завдання, що доповнюють і розширюють основні спільні завдання. При цьому можлива допомога учням при розв’язувані ними важких задач з використанням “підказок” – допоміжних питань і задач. Перед тим, як пропонувати “підказку”, треба добре знати як проходить розумовий процес, в якому місці задачі учень може мати затруднення (труднощі). Заздалегідь оформлена “ підказка ” дозволяє організувати самостійну роботу сильних школярів без вчителя, який в цей час має можливість займатись іншими групами учнів. “ Підказка ” спільної ідеї розв’язування складається, як правило, з вказівки незвичайного співставлення даних, шуканих. Допомога в таких випадках може бути надана вказівкою, які дані необхідно зіставити, в якому руслі отримати висновок, яку теорему необхідно використовувати, яку теорему і до якого об’єкту треба застосувати.

          Для того, щоб успішно це здійснити, можна застосовувати певну систему тестових вправ, що мають метою перевірити:

1) рівень навченості;

2) вміння самостійно працювати;

3) уміння читати з розумінням і потрібною швидкістю навчальний текст;

4) здатність до кмітливості;

5) рівень розвитку того чи іншого компонента математичного мислення;

6) пізнавальні інтереси і т.п.

В якості прикладу наведемо декілька завдань для учнів 8 класу, що мають на меті перевірити рівень логічного мислення.

1. Вираз має зміст при

а) всіх значеннях, крім;

б) всіх значеннях.

2. Щоб додати раціональні дроби з однаковими знаменниками треба:

а) додати їх чисельники та знаменники;

б) додати їх чисельники, а знаменник залишити той самий;

в) додати їх знаменники, а чисельник залишити той самий;

г) додати їх чисельники, а знаменники перемножити.

3. Прямокутник — це:

а) чотирикутник, у якого всі кути рівні;

б) паралелограм, у якого всі кути прямі;

в) паралелограм, у якого всі сторони рівні;

г) чотирикутник, у якого всі сторони рівні;

д) паралелограм, у якого всі сторони паралельні.

4. Протилежні сторони паралелограма …

а) паралельні;

б) перпендикулярні;

в) вертикальні;

г) суміжні;

д) рівні.

Застосування таких тестів дає вчителю можливість вивчити динаміку розвитку кожного школяра і підібрати потім систему конкретних завдань для його індивідуальної роботи.

 

 ТЕХНОЛОГІЯ РІВНЕВОЇ  ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ

 

Використання рівневої диференціації навчання вносить значні зміни в навчальний процес, які проявляються не стільки в методичних прийомах, які застосовує вчитель,  скільки в зміні стилю взаємодії з учнями.

В умовах технології рівневої диференціації учень – це, перш за все, партнер, який має право на прийняття рішень (на вибір  змісту своєї, освіти, рівня його засвоєння і т.п.). Природно, що відповідальності за виконання прийнятого рішення лягає на учня. Головна ж задача і обов’язок учителя – допомогти дитині прийняти і виконати прийняте їм рішення; допомогти зробити правильний вибір, визначитися в сфері своїх пізнавальних інтересів, допомогти скласти або скоректувати програму самоосвіти, підібрати потрібну літературу, поставити пізнавальну задачу, адекватну інтересам і можливостям учня, своєчасно його проконсультувати і проконтролювати; нарешті, забезпечити своєчасне досягнення кожним, як мінімум обов’язкового рівня загальноосвітньої підготовки.

При цьому дана технологія не обмежує вчителя в виборі методів, засобів і форм навчання – все це знаходиться повністю в компетенції вчителя. Разом з тим слід пам’ятати, що ті чи інші педагогічні рішення вчителя не повинні перекреслювати основні принципу технології, основою якої є рівнева диференціація.

Необхідні умови організації учбового процесу:

• у вимогах до підготовки учнів з предмету виділяється базовий рівень, що задає обов’язкові результати навчання; обов’язкові результати навчання визначаються по кожній темі курсу;
• виділений рівень повинен бути реально досяжним, посильним для учнів;
• з самого початку вивчення теми до учнів необхідно донести вимоги до обов’язкової підготовки, якої вони повинні досягти в результаті навчання, сформульованих у вигляді конкретних учбових завдань:
• учбовий процес зорієнтовується так, щоб всі учні змогли досягти обов’язкових результатів навчання по кожній темі;
• рівень, до якого доводиться викладання, повинен перевищувати рівень обов’язкових вимог до засвоєння матеріалу; це необхідно і для досягнення обов’язкової підготовки, і для забезпечення потреб учнів, що мають здібності та цікавляться математикою.

Учбово-виховний процес будується на основі поваги до учня як особистості, за цим визначаються не тільки обов’язки (зокрема засвоєння матеріалу на обов’язковому рівні), але і права. Найважливішим з них є право вибору – отримати у відповідності до своїх здібностей підвищену підготовку з предмету чи обмежитись обов’язковим рівнем його засвоєння; у тому числі і в системі контролю необхідно дотримуватись цих умов (висвітлення вимог до обов’язкової підготовки, їх посильність та відкритість для учнів, можливість підвищеної підготовки і т.д.). Важливою функцію контролю стає не тільки фіксація рівня навченості, але й стимулювання досягнення тієї підготовки, яку учні спроможні отримати при вивченні шкільних дисциплін.

Реалізувати у практиці викладання принципи рівневої диференціації можливо, використовуючи різні методи і форми навчання, різні прийоми роботи з учнями. Додержання вказаних вище принципів рівневої диференціації є обов’язковим для вчителя, який працює в рамках даної технології.

          Багато можливостей для диференціації на етапі закріплення та застосування знань є й у індивідуалізованої самостійної роботи. При організації індивідуалізованої самостійної роботи вчитель може керуватися наступними схемами:

Схема 1:

1) Загальні завдання;

2) Додаткові завдання більш швидким і сильним учням.

Схема 2:

1) Загальні завдання;

2) Розгалужені завдання

— Більш легкий варіант

— Середній варіант

— Важчий варіант.

Схема 3:

— Розгалужені завдання

— Більш легкий варіант

— Середній варіант

— Важчий варіант.

Схема 4:

1) Розгалужені завдання

— Більш легкий варіант

— Середній варіант

— Важчий варіант.

2) Загальні завдання.

Використання схеми 1) доцільно при вивченні такої нової теми, яка містить багато нового навчального матеріалу і тому змушує бути в напрузі не тільки слабких, але й сильних учнів. Схема враховує різний темп просування учнів і на закінчення пропонує додаткові завдання більш швидким учням.

Схема 2) ефективна тоді, коли не представляється доцільним змушувати всіх учнів у повному обсязі виконувати спільні завдання, оскільки це виявилося б для частини учнів занадто легким, а для частини — занадто важким. Схема прийнятна, наприклад, в тому випадку, коли новий матеріал містив елементи повторення або коли мають справу з вправами після проходження теоретичних основ теми.

Схема 3) використовується тоді, коли підготовка і здібності учнів настільки різні, для засвоєння нового матеріалу, що загальні завдання не можуть забезпечити розвиваючої діяльності для більшості учнів. Такий стан типово для повторення, а також у разі занадто різних попередніх знань.

Схема 4) доцільна в тому випадку, коли між учнями спостерігаються великі відмінності в таких попередніх знаннях, які необхідні для вивчення нового навчального матеріалу. У такому випадку розгалужені завдання готують сприйняття і розуміння нової теми, а їх виконання сприяє переходу до загальних завдань.

           Крім того, можна використовувати різні комбінації цих схем.

РЕАЛІЗАЦІЯ РАЗВИВАЮЧОГО НАВЧАННЯ ПРИ НАВЧАННІ МАТЕМАТИКИ (ТИПИ УРОКІВ).

           Реалізація розвиваючого навчання полягає в тому, що вчитель не тільки використовує різні методи і форми роботи з учнями на уроці, але і систематично навчає  їх способам використання тих чи інших видів навчально – пізнавальної діяльності. З точки зору психології  в забезпеченні належних умов для успішного формування математичних понять важливе значення відводиться попередньому досвіду і знанням учнів. І тому, в процесі подачі нового матеріалу (на уроках закріплення) вчитель повинен орієнтуватись як його учні знають попередній матеріал, а які моменти викликають у них труднощі. Тому такі уроки слід починати з актуалізації  опорних знань і способів дій: дітям буде легше зорієнтуватись у новому, це спростить розв'язування  математичних вправ, матеріал буде повторюватись і систематизуватись. Важливим є також те, що при повторному  відтворенні тієї чи іншої навчальної  інформації діти вчаться виділяти головне, відкидаючи другорядне. Тому необхідно, правильно організувавши  закріплення матеріалу, неперервно повторювати на протязі всього навчального року, а не тільки проводити підсумкове повторення в кінці теми, чверті чи навчального року.

  Необхідно, щоб дітям було цікаво вчитися. А це можливо лише тоді, коли матеріал зрозумілий і доступний, а це, в свою чергу, досягається  через повторення, систематизацію і узагальнення навчального матеріалу. Як було сказано вище, на кожному уроці це впроваджується    на етапі актуалізації знань і умінь.

 Відповідно до  основної дидактичної мети, уроки поділяються на чотири типи:

1.   ознайомлення з новим матеріалом;
2.   закріплення вивченого;
3.   перевірки знань, умінь та навичок;
4.   систематизації та узагальнення вивченого матеріалу.

Також часто застосовується комбінований урок, в межах якого проводиться ознайомлення з новим матеріалом та закріплення знань.

Структура 1) - 3) типів уроків включає в себе етап актуалізації опорних знань і умінь.

 Тип уроку вказує, з якою метою і в якій формі проводити актуалізацію, яка передбачає не тільки відтворення раніше вивченого, але й застосування попередніх знань у нових ситуаціях, їх поглиблення, активізацію пізнавальної діяльності учнів, тощо.

Урок ознайомлення з новим матеріалом

Актуалізація на цьому уроці проводиться з метою повторення та застосування раніше вивченого матеріалу у нових ситуаціях.

 Якщо подача нового матеріалу іде не в одній темі чи розділі математики і є новою для учнів, то використовувати рівневий  підхід на цьому етапі не слід. Учні повинні засвідчити обов’язковий рівень знань, тобто всі диференційовані групи в класі повинні володіти матеріалом, без якого подальше навчання неможливе. В цьому випадку актуалізацію знань можна провести у формі фронтального опитування. Дітям пропонується  система питань, на які вони повинні відповісти.

 Якщо ознайомлення з новим матеріалом відбувається в межах  однієї теми, то актуалізацію проводять у різних формах, враховуючи різнорівневий  підхід до навчання. Наприклад, роботу можна організувати так:

1.         Фронтальна перевірка теорії.
2.         Перевірка вмінь:

 - з групою учнів початкового та середнього рівнів  засвоєння знань проводиться усна робота репродуктивного характеру (користуючись правилом чи формулою, виконати  обчислення, зробити малюнок або пояснити його, тощо);

 - для учнів достатнього рівня засвоєння матеріалу пропонують питання проблемного характеру;

 - учням високого рівня засвоєння знань дають завдання на картках творчого характеру.

Після завершення усної фронтальної роботи з першою групою, всі слухають відповіді на питання  учнів другої групи. Вчитель сам перевіряє правильність відповідей, або доручає це  учням високих рівнів підготовки.

 

Урок закріплення вивченого

Актуалізація проводиться з метою відтворення раніше вивчених знань і способів дій під час перевірки домашнього завдання (перевіряється засвоєння матеріалу, з яким учнів знайомили на  попередніх уроках), як теорії, так і практичних завдань, або пропонується система вправ, при розв’язуванні яких необхідно виявити знання фактичного матеріалу.

 Використовуючи диференційований підхід, побудувати перевірку домашнього завдання можна таким чином.

1. - Фронтальне опитування теоретичних знань.

    - Домашні вправи достатнього та високого рівнів складності, кілька учнів відповідного рівня засвоєння знань, можуть представити на дошці.

2. Будь-який учень розв’язує домашні вправи біля дошки, відповідає на теоретичні запитання, а учень вищого рівня засвоєння знань рецензує відповідь товариша (за планом, запропонованим вчителем) та оцінює її.

3. Вчитель працює з учнями початкового та середнього рівнів засвоєння матеріалу, решта класу виконують завдання на картках, аналогічні домашнім вправам чи подібні їм. Коли педагог пропонує систему вправ для роботи, то учні високого рівня засвоєння знань повинні розв’язати всі задачі, учні достатнього рівня – крім найскладнішої, середнього рівня – декілька нескладних вправ. Тобто різні диференційовані групи  одержують різні за складністю завдання, "обмежені знизу" обов’язковим рівнем знань і умінь з даної теми.

Урок перевірки знань, умінь та навичок

 Актуалізація  на цьому уроці проводиться з метою перевірки засвоєння знань, умінь та їх систематизації.

 Оскільки дана проблема не набула розголосу в педагогічній літературі, то на нашу думку, актуалізацію слід організовувати наступним чином.

 Якщо на даному уроці запланована  самостійна робота (45 хв.), то доцільним буде  проведення фронтального опитування всіх учнів з даної теми. Якщо ж робота розрахована не на весь урок, то початок його можна відвести повторенню, використавши диференційований підхід. Решта часу  відводиться для самостійного розв’язування вправ, враховуючи особливості кожної  диференційованої групи.

 Якщо ж даний урок – це контрольна робота, то маємо справу з "внутрішньою" актуалізацією знань і умінь ( кожен учень, готуючись до уроку, повторює навчальний матеріал з даної теми). В разі необхідності, можна провести консультацію для "слабших" учнів напередодні контрольної, щось на зразок розширеної актуалізації знань та умінь.

 Якщо даний урок проходить як інтегрований залік, то тоді в цьому випадку повністю працює різнорівневий підхід до навчання: учні повинні володіти матеріалом у відповідності з вибраним рівнем засвоєння матеріалу.

 

Комбінований урок

 На цьому уроці подається новий та  закріплюється раніше вивчений матеріал. Актуалізація проводиться з метою виявлення засвоєння учнями певного рівня знань і умінь у формі  перевірки домашнього завдання ( як теорії, так і практики ), або розв'язування  вправ, які охоплюють знання визначеної теми з урахуванням диференційованого підходу.

 Для того, щоб активізувати пізнавальну діяльність учнів, зацікавити  дітей навчанням, використовують нетрадиційні форми уроків, інтерактивні методи навчання. Тут необмежені можливості для використання диференційованого підходу на всіх етапах уроку. Так, наприклад, урок ознайомлення з новим матеріалом можна провести у формі конференції, усного журналу "Незвичайне поруч", "Подорож у країну не відгаданих таємниць", клубу "Що? Де? Коли?", дидактичного театру; урок закріплення – як роботу штабів знань, роботу в парах, групах, ланках, урок виправлення помилок, урок творчості; перевірку знань можна  організувати  як пізнавальний КВН, аукціон знань, мозковий штурм, захист фантастичних проектів, конкурс шпаргалок. Тут основну роль мають відіграти "сильні учні" (як правило, вони відвідують математичний гурток або факультатив). Для них це – творча робота, пошук, знайомство з новою літературою і невідомими фактами…

 Для учнів початкового та середнього рівнів засвоєння знань це теж дуже цікаво, бо вони виступають у ролі глядачів, дізнаються про невідоме в математиці, чи просто змагаються між собою у знаннях. Актуалізація на таких уроках проводиться з метою повторення основних ідей теми, щоб учні могли вільно орієнтуватися у поставлених питаннях, щоб їм був зрозумілим матеріал, а, отже, і цікавіше на уроці.

 Наприклад, урок перевірки знань, умінь і навичок можна провести у формі КВН. Клас  ділять на три команди (не за рівнями, а, наприклад, по рядах), і з сильних учнів вибирають троє консультантів, які допомагають вчителеві проводити КВН.

 Структура уроку:

1.         Привітання команд
2.         Розминка
3.         Бліц – турнір
4.         Конкурс художників
5.         Конкурс капітанів
6.         Конкурс консультантів
7.         Підсумки

 Актуалізація проходить у формі розминки. Кожна команда одержує завдання, яке треба кожному виконати письмово (підбираються декілька простих вправ на безпосереднє застосування теорії, відповідної теми, на практиці).

 Кожен консультант слідкує за своєю командою, збирає аркуші з завданням, перевіряє та оцінює їх. Завдання повинні бути підібрані такі, які б вимагали присутності у командах дітей з різними рівнями засвоєння знань.

 Уроки систематизації і узагальнення вивченого матеріалу у своїй структурі не містять етапу актуалізації знань. На цих уроках іде загальне повторення вивченого, узагальнюються основні знання з теми чи розділу, виводиться висновок про місце їх у системі математичних знань в цілому.

 Урок буде більш результативним, якщо групову роботу поєднувати з фронтальною та індивідуальною формами навчання. Є різні варіанти такого поєднання. Наприклад, ефективним є взаємозв’язок вигляду:

1. фронтальна форма – групова недиференційована – індивідуальна;
2. групова форма – фронтальна форма – індивідуальна.

Головна  функція вчителя за групової навчально-пізнавальної діяльності учнів полягає в організації співробітництва учнів в групах. Таке співробітництво передбачає:

1. розподіл обов’язків між учнями;
2. аналіз завдання, взаємо обмін інформацією;
3. взаємодопомога, взаємоперевірка та взаємо оцінювання один одного.

Учитель повинен дбати про високий навчальний потенціал кожної групи. Для цього доцільно добирати диференційовані завдання, враховуючи навчальні можливості кожного учня. Якщо ж завдання виявилося для учня складним, то слід замінити його на простіше, більш доступне для учня; важке завдання учень за бажанням може виконати вдома, попередньо проаналізувавши його з учителем.

 Групова навчальна діяльність учнів на етапі актуалізації знань та способів дій має значні переваги в порівнянні з іншими методами, а саме:

1) допомагає створювати на уроці умови для формування позитивної мотивації навчання школярів;

2) дає можливість здійснювати диференціацію навчання;

3) сприяє виробленню вмінь співпрацювати з іншими учнями;

4) забезпечує високу активність усіх учнів;

5) реалізує їх природне прагнення до спілкування, взаємодопомоги і співпраці;

6) підвищує результативність навчання та розвиток школярів.

 

  ВИСНОВОК

 

Диференціація навчання досягається шляхом забезпечення кожного учня навантаженням, відповідно з його індивідуальними можливостями, що практикується різними способами: диференційовані домашні завдання. необов’язкові завдання, додаткові індивідуальні завдання.

Навчальний процес повинен не просто пристосовуватись, підбудовуватись під власний рівень знань і умінь учнів, змінюючи зміст і методи, а орієнтуватись на досягнення максимально важливих результатів кожним учнем і, що не менш важливе, на розвиток мислення, пізнавальних можливостей, інтересів.

Отже, організація індивідуального підходу до навчання математиці є одним із складних питань, в якому пов’язані теоретичні, частіше не до кінця розв’язані питання, і практичні вимоги їх реалізації на конкретному предметі, в конкретних класах.

Для організації індивідуального підходу учителю необхідно таке: мати уяву про особливості розумової діяльності рівних груп учнів, про шляхи розвитку мислення, уміти оцінювати рівень розвитку учнів, уміти здійснювати допомогу різної міри, якщо учні натрапляють на труднощі, володіти формами організації індивідуального підходу з урахуванням необхідності розвитку мислення.

 ДОДАТОК

 Тема "Квадратична функція"

 

Номер уроку	Тема уроку	Кількість годин
1	Функції та їх властивості	1
2	Властивості функцій	1
3-4	Найпростіші перетворення графіків функцій	2
5	Графіки функцій, що містять знак модуля	1
6	Квадратний тричлен, його корені	1
7-8	Розкладання квадратного тричлена на лінійні множники	2
9	Виділення квадрата двочлена з квадратного тричлена	1
10	Найбільше і найменше значення квадратного тричлена	1
11	Тематичне оцінювання. Контрольна робота	1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок 1. Функції та їх властивості

Мета. Узагальнити та розширити знання учнів про функції та їх властивості

Тип. Комбінований урок

 Актуалізацію опорних знань спочатку проводимо у формі фронтального опитування.

1.Яка залежність між змінними називається функціональною або функцією?

2.Що таке аргумент(незалежна змінна)?

3.Наведіть приклади функцій.

4.Як знайти область визначення функції? область значень?

5.Які ви знаєте способи завдання функції?

6.Що таке графік функції? Як його побудувати?

7.Які властивості функції легко побачити з її графіка?

8.Чи можна за графіком функції знайти її значення при заданому значенні аргументу? Як?

9.Чи кожна лінія в координатній площині задає функцію, тобто є графіком деякої функції?

10.Як розпізнати графік функції?

 Далі учні початкового (далі - у.п.р.) та середнього (у.с.р.) рівнів навчальних досягнень працюють з вчителем, розв’язуючи №№  ….

 Учні достатнього (у.д.р.) рівня підготовки працюють над № …, високого (у.в.р.) - №№ … (по одному представнику  на кожен № готуються біля дошки). Потім вони коментують розв’язання заданих вправ для учнів з іншим рівнем підготовки.

 

Урок 2. Властивості функцій

Мета. Закріпити знання  учнів про функції та їх властивості

Тип. Урок закріплення вивченого

1. Перевірка д/з та опитування учнів

- Яка функція називається зростаючою? спадною? парною? непарною?

- Що таке область визначення функції? область значень?

2. № … розв’язує вчитель з детальним поясненням

   № … - у.п.р. та у.с.р.

   № … - у.д.р. та у.в.р.

3. Тест " Функції та їх властивості "

   П.р.

   1. Функція у = ∫ (х) наз. зростаючою, якщо з того, що х ‹ х ,випливає, що

    а) у  › у  ; б) у   ≥ у  ; в) у  ‹ у  .

   2. Функція наз. парною, якщо її область визначення симетрична відносно нуля і :

    а) ∫ (-х) = │∫ (х)│; б) ∫ (-х) = ∫ (х); в) ∫ (-х) = - ∫ (х).

   3. Графік непарної функції  симетричний відносно:

    а) осі Ох; б) осі Оу; в) початку координат.

    С.р.

   4. Відомо,що функція у = ∫ (х) спадна на проміжку │-10;10│. Порівняти:

    а) ∫ (4) і ∫ (5);  б) ∫ (-3) і ∫ (-7).

   5. На яких малюнках зображено графіки парних функцій:

    

  6. На яких малюнках зображено графіки спадних функцій?          

  Д.р.

      7. Функція, графік якої зображено на малюнку е), зростає на:

         а) (-4;0) і (1;3);                                  б) на всій області визначення;

         в) (-3;3);                                г) (0;4).

        8. Областю визначення функції у = √ 5- 2х є проміжок:

         а) │0;+∞);            б) (-∞;2,5│;          в) │2,5;+∞).

        9. Які з даних функцій є непарними:

         а) у = 3х + 1;          б) у = 2/х;           в) у = х  - х;         г) у = х   + 4.

        10. Які з даних функцій зростають на всій області визначення:

         а) у = √ х + 1;         б) у = х  ;            в) у = х – 2;          г) у = 4 – 3х.

          В.р.

        11. Знайти найбільше значення функції у = х  + 3 на проміжку │-5;-3 │.

        12. Функція у = х   - 3х зростає:

          а) на всій осі;                                    б) (0; +∞)

          в) (-∞; -1) та ( 1; +∞);                          г) (-1; 1).

 

Урок 3. Найпростіші перетворення графіків функції

Мета. Формування вміння побудови графіків функцій у = а ∫ (х) за графіком функції у = ∫ (х)

Тип. Урок ознайомлення з новим матеріалом

     Поки  троє учнів біля дошки готують д/з ( по одному завданню з кожної вправи ), з класом проводиться бесіда, в якій повторюються означення функції, її властивості.

     Далі розпочинається вивчення нового матеріалу.

 

Урок 4. Найпростіші перетворення графіків функції

Мета. Формування вміння побудови графіків шляхом перетворень

Тип. Комбінований урок 

 Фронтальне опитування (на дошці представлені малюнки, які треба співвідносити із запитаннями)

- Як розміщені графіки функції у = ∫ (х) та у = -∫ (х)?

- Як побудувати графік функції у = -∫ (х), маючи графік функції у = ∫ (х)?

- В якому випадку графік у = к ∫ (х) одержується розтягуванням графіка

у = ∫ (х),  а в якому – стисканням?  Відносно якої осі ?

- Як з графіка функції у = ∫(х) одержати графік функції у = к∫(х) при  к›│ 1│?, при к‹ │ 1│?

  

 

Урок 5.  Графіки функцій, що містять знак модуля

Мета. Формування навичок побудови графіків функцій з модулями

Тип. Комбінований урок

 Троє учнів (у.д.р. або у.в.р.) біля дошки виконують д/з – кожен по 2 графіка. Після побудови графіка вказують множину значень, корені (нулі), проміжки знакосталості, проміжки зростання і спадання функції.

 З класом (у.с.р. та у.п.р.) тим часом повторити, коли графік функції зміщується вгору, вниз, вліво, вправо; як перетворити вираз ах² +вх +с, щоб графік квадратичної функції одержати з параболи у=х ².

 Далі актуалізацію опорних знань проводимо для всіх учнів класу.

- Що наз. модулем числа?

- Чому дорівнює │х-а│? │-х│?

- Яких значень набуває вираз │х│?

Записи:

                 х, якщо х≥0.                                                   х-а, якщо х≥а,

│х│=                                                         │х-а│=      

                 -х, якщо х‹0.                                                   а-х, якщо х‹а.

 

 

Урок 6.  Квадратний тричлен, його корені

Мета. Формування поняття квадратного тричлена

Тип. Комбінований урок

 Учні об’єднуються  в групи за рівнем навчальних досягнень.

Побудувати графік функції.

 

І група (у.с.р. та у.п.р.)

                                        3, х ≤ 3

а) у = │х - 3│ + х =       2х – 3, х > 3

 

б) Побудувати графік функції у = │х² - 4│.

Будується графік у = х² - 4 і нижня частина відбивається симетрично відносно ох.

ІІ група (у.д.р. та у.в.р.)

а) у = │х – 1│ +│х - 3│.

Вирази, що стоять під знаком модуля, перетворюються в нуль у точках 1 і 3.

 1) х  ≤ 1          │х - 1│ = 1 – х; │х - 3│ = 3 – х; у = 4 – 2х.

 2) 1 ≤ х ≤3       │х - 1│= х – 1;│х – 3│ = 3 – х; у = 2.

 3) х > 3         │ х – 1│= х – 1; │х – 3 │= х – 3;  у = 2х -4.

Графік функції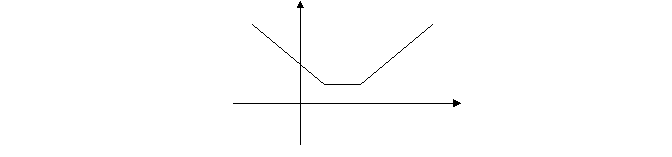

б) у = х² - 3│х│ + 2. Оскільки х² = │х│², то будується графік функції

 у= х² -3х +2 для х ≥0 і відбивається симетрично осі Оу.

 Після роботи в групах, по 2 учні з кожної виходять до дошки і пояснюють порядок побудови запропонованих графіків.

 Далі починаємо пояснення нового матеріалу.

 

 

Урок 7. Розкладання квадратного тричлена на лінійні множники

Мета. Формування вміння розкладання квадратного тричлена на лінійні множники

Тип. Урок вивчення нового матеріалу

 Актуалізація опорних знань виконується усно. Проводимо фронтальну бесіду, в процесі якої повторюється означення квадратного тричлена, його коренів, пряма та обернена теореми Вієта.

 

Урок 8.  Розкладання квадратного тричлена на лінійні множники

Мета. Формування вміння розкладання квадратного тричлена на лінійні множники

Тип.  Урок закріплення вивченого

 Актуалізація опорних знань – тест " Квадратний тричлен ".

П.р.

1.Які з даних виразів є квадратними тричленами:

а) х²+3х -1;                   б) х³ -х +2;                       в) 4 - х²;                     г) х² +х +1/х.

2.Які з тричленів набувають числового значення, рівного 2, при х = - 1:

а) х²-4х -7;                    б) 3 - х²;                              в) х² +х + 2;                г) 3х²- х -2.

3. Коренями тричлена х² + х – 6 є числа:

а) -2 і 3;                         б) 2 і -6;                              в) -3 і 2;                    г) -3 і 1.

С.р.

4. Які з квадратних тричленів не мають дійсних коренів:

а) х² +х +1;                    б) х² +х -1;                          в) х² +5;                    г) х² -4.

5. Тричлен х²-4х +1:

     а) не має дійсних коренів;

     б) має один корінь;

      в) має два корені.

6. Добуток (2х+3)(х-1) є розкладом на множники квадратного тричлена:

а) 2х² +5х -3;                 б) х² +х -3;                          в) 2х² +х +3;             г) 2х² +х -3.

Д.р.

7. Не можна розкласти на лінійні множники квадратні тричлени:

а) х² -х +2;                      б) х² +х -2;                          в) х² -2х +4;             г) х² -4.

8.Тричлен 2х² + х + р розкладається на множники 2(х+1)(х-1/2), якщо р має числове значення:

а)1;                                  б) -2;                                   в) -1;                                 г) 2.

9. Тричлен х² -2х -8 розкладається на множники (х-4)(х-к), де к має значення:

а) -2;                                б) 2;                                     в) 1;                                 г) 4.

В.р.

10.При скороченні дробу (6х² +х -2)/(3х+2) одержимо:

а) 2х -1;               б) 1- 2х;                     в) 2х +1;                     г) дріб нескоротний.

11. Для того, щоб дріб (х²-5х+р)(х-2) можна  було скоротити, числове значення р має дорівнювати:

а) -6;                                б) 4;                                    в) 6;                                    г) 8.

12. Не можна скоротити дроби:

а)(х²+х+1)/(х+1);                 б)(х²+2х+1)/(х+1);                              в)(х²+х-2)(х+1).

 

 

 

Урок 9. Виділення квадрата двочлена з квадратного тричлена

Мета. Формування вміння виділяти квадрат двочлена

Тип. Комбінований урок

Інтерактивна вправа "Обери позицію"

-У чому полягає спосіб розв’язування квадратних рівнянь виділенням квадрата двочлена?

- Як вивести формулу коренів квадратного рівняння?

- З якого тричлена при цьому виділяється квадрат двочлена?

- Квадрат якого двочлена виділяється?

- Навести приклади

 

 

Урок 10. Найбільше і найменше значення квадратного тричлена

Мета. Формування вміння знаходити найменше чи найбільше значення квадратного тричлена

Тип. Комбінований урок

1. Фронтальне опитування (інтерактивна вправа "Мікрофон"):

  - Що таке квадратний тричлен?

  - Як знайти значення квадратного тричлена при заданому значенні х?

   - Обчислити значення тричленів х²-6х+5 та -х² +4х-1 при х рівному 0;1;2;3;4. Розв'язки оформити у вигляді таблиці (двоє учнів працюють біля дошки)

                      

х	0	1	2	3	4
х²-6х+5	5	0	-3	-4	-3

х	0	1	2	3	4
-х²+4х-1	5	0	-3	-4	-3

 

2. Інтерактивна вправа "Обери позицію":

 Запитання до першого учня:

  - Яке найменше значення тричлена на заданій множині?

  - Чи може він набувати значень, менших за -4, при інших значеннях х?

 Запитання до другого учня:

   - Яке  найбільше значення тричлена на заданій множині?

   - Чи може він набувати значень, більших за 5?

На друге запитання учні можуть відповісти по-різному. Відповідь "не знаю" приймається з метою мотивації вивчення нового матеріалу.

 

 Більшість уроків з алгебри - комбіновані. Тому актуалізація опорних знань на алгебрі відбувається як перевірка д/з. У цьому випадку добре працює різнорівневий підхід до навчання, адже кожна з диференційованих груп одержує своє д/з.

 Від учнів початкового та середнього рівня оволодіння знаннями не слід вимагати виведення формул, розв’язування складних вправ, досить обмежитися знанням основних принципів та безпосереднього застосування теорії.

 Учням достатнього та високого рівнів засвоєння знань доречно показати нестандартні методи чи способи розв’язання та уміти застосовувати ці знання при розв’язуванні складніших, багатокрокових вправ.

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

 

1.   Бевз Г.П. Методика викладання математики. - Вища шкл., К., 1989
2.   Сліпкань Г.А. Методика викладання математики.
3. Болтянський В.Г., Глейзер Г.Д. К проблеме дифференциации                      школьного математического образования //Математика в школе. -1988.
4. Дорфеев Г.В., Кузнецова А.В., Суворова С.Б., Фирсов В.В. Дифференциация обучения математике // Математика в школе .1990. №5.
5.   Фарков А.В. К проблеме профильной дифференциации в малокомплектной школе //Математика в школе. - 1991.
6.     Державний стандарті базової та повної загальної середньої освіти.
7.   Мазур Г.В. Використання диференційованого підходу на різних етапах уроку: //// Пед. пошук. – 1994. – №26
8.   Черних Л.В.  «Диференційований підхід у навчанні математики». Газета «Математика», 2003.
9.   Матеріал взято з :http://coolreferat.com/Диференціація навчання на всіх етапах уроку.
10.  Математика : Підруч. для 5 кл.загальноосвіт.навч. закладів/ О.С.Істер. – К. : Генеза, 2013
11.  Математика : Підруч. для 6 кл.загальноосвіт.навч. закладів/ О.С.Істер. – К. : Генеза, 2014
12.  Буковська О.І. Математична логіка. 5 – 9 класи. – Х.: Вид. група " Основа ", 2005. – 176 с. – ( Серія " Бібліотека журналу " Математика в школах України " "; Вип. 11 ( 35 )
13.  Вихор Світлана, Гап'юк Галина. Тематичні та контрольні роботи з алгебри. 9 клас. – Тернопіль: Підручники і посібники, 2003. – 48 с.
14.  Газета Математика (2002 р. №20)
15.  Голодюк Л.С. “ Рівнева диференціація на уроках геометрії”.
16.  Гордієнко В.М., Алєксєйчук Ф.В. Уроки з математики в дев'ятому класі. – Кам'янець – Подільський: Абетка, 2002. – 124 с.
17.  Эрдниев П. М. "Укрупнение дидактических единиц в обучении математики". (Видавництво "Просвещение")
18.  Иржавцева В. П. "Систематизация и обобщение знаний учащихся в процессе изучения математики. (Видавництво "Радянська школа")
19.  Капіносов А.М. Геометрія 9. Дидактичні матеріали для рівневого навчання. – Кам'янець – Подільський: Абетка – НОВА, 2001. – 144 с.
20.  Карпінська І.Й. Нестандартні уроки з математики. – Тернопіль: Підручники і посібники, 2000. - 48 с.