АНАЛІЗ ТИПОВИХ ПОМИЛОК ПРИ РОЗВ’ЯЗУВАННІ РАЦІОНАЛЬНИХ РІВНЯНЬ З ПАРАМЕТРАМИ В ОСНОВНІЙ ШКОЛІ

АНАЛІЗ ТИПОВИХ ПОМИЛОК ПРИ РОЗВ’ЯЗУВАННІ

РАЦІОНАЛЬНИХ РІВНЯНЬ З ПАРАМЕТРАМИ В ОСНОВНІЙ ШКОЛІ

Лінія рівнянь і нерівностей є однією з основних ліній шкільної математичної освіти. Зокрема, в основній і старшій школі учні отримують знання про різні види алгебраїчних і неалгебраїчних рівнянь та нерівностей та про методи їх розв'язання. Поглиблене вивчення математики в основній школі передбачає також вивчення теми «Раціональні рівняння та нерівності з параметрами», яка має важливе теоретичне та прикладне значення, розвиває цілий спектр навичок, зокрема, вміння обчислювати, перетворювати, аналізувати, порівнювати.

Вивчення цієї теми починається у 8-му класі при розв'язуванні з лінійних та раціональних рівнянь з параметрами і продовжується розглядом квадратних рівнянь з параметрами. Під час вивчення теми «Квадратична функція» у 9-му класі передбачено розв'язування задач на дослідження властивостей квадратного тричлена, а також застосування графічних прийомів розв'язування задач з параметрами.

Задачі з параметрами в силу цілого ряду причин розглядаються в школі досить рідко, проте включаються до завдань державної підсумкової атестації для класів з поглибленим вивченням математики та до завдань ЗНО. Це пояснюється не лише важливістю самого питання, але і можливістю на одному прикладі перевірити знання учнів з різних розділів елементарної математики та їх логічне мислення.

Розв’язати рівняння (нерівність) з параметрами – означає вказати, при яких значеннях параметрів існують розв’язки і які вони, а також вказати, при яких значеннях параметрів рівняння не має розв’язків.

Суттєвим етапом розв’язання задач з параметром є запис відповіді. Відповідь – це систематизація та узагальнення раніше одержаних результатів. І дуже важливо відобразити у відповіді всі етапи розв’язання. Запис відповіді здійснюється у формі: “якщо ..., то ...”, або “..., якщо ...”.

У зв’язку з тим, що в основній школі приділяється не велика увага вивченню теми  «Раціональні рівняння та нерівності з параметрами», більшість учнів та абітурієнтів або взагалі не вміють розв’язувати завдання з параметрами, або припускаються різноманітних помилок. Їх причини зводяться до поверхневого або чисто формального розуміння основних властивостей нерівностей, або пов’язані з недостатніми навичками тотожних перетворень.

Окрім того, при розв’язуванні рівнянь із параметрами учні не враховують допустимі значення параметрів, які входять до рівняння, не враховують область допустимих значень невідомого, не роблять перевірку знайденим значенням по відношенню до ОДЗ, не розглядають всі можливі випадки. Розглянемо деякі приклади.

Приклад 1. Розв’язати рівняння відносно :

.

Неправильне розв’язання

Відповідь: .

Правильне розв’язання

Основою розв’язання задач з параметрами є правильне розбиття області зміни параметра на окремі частини і до цього потрібно привчати учнів.

У запропонованому рівнянні коефіцієнт при дорівнює . Тому можливі такі випадки:

1) Якщо коефіцієнт при дорівнює нулю і рівняння має вигляд

та не має коренів;

 2) Якщо коефіцієнт при не дорівнює нулю; тоді поділимо обидві частини рівняння на коефіцієнт :

,

,

.

 Відповідь: якщо , то рівняння розв’язків не має; якщо , то .

 Коментар. Важливо звертати увагу учнів на випадки, коли коефіцієнт при дорівнює нулю, і розглядати їх у першу чергу, що допоможе учням уникати поширеної помилки: взагалі не розглядати таких випадків.

Приклад 2. Розв’язати рівняння .

Неправильне розв’язання

Відповідь: .

Коментар. Залишилося нез’ясованим, при яких значеннях і рівняння має розв’язки, тобто розв’язання рівняння фактично не доведено до кінця.

Правильне розв’язання

1) Якщо , то ділення на завжди можливе й рівняння має єдиний розв’язок: .

2) Якщо і , то рівняння розв’язків не має.

3) Якщо і , то рівняння задовольняє будь-яке значення .

Приклад 3. Розв’язати рівняння .

Неправильне розв’язання

;

.

Коментар. Учні не враховують, що рівняння містить параметр і рівняння з параметром – це, по суті, множина рівнянь. У данному випадку міркувати так. Перед тим як ділити обидві частини рівняння на коефіцієнт при невідомому, подивимося, чи не може при деяких значеннях параметра цей коефіцієнт перетвориться в нуль. Помічаємо, що тричлен перетворюється в нуль, якщо , . Отже, потрібно окремо розглянути ці випадки.

Правильне розв’язання

Покладемо . Рівняння набере вигляду . Коренем цього рівняння є будь-яке дійсне число.

Якщо , рівняння набирає вигляду . Це рівняння не має розв’язків.

Якщо, , , то можна обидві частини рівняння розділити на коефіцієнт при , одержимо:

.

Відповідь: якщо , то – будь-яке дійсне число; якщо , то розв’язків не має; якщо , , то .

Щоб зменшити кількість помилок при розв’язанні лінійних рівнянь з параметрами корисно їх розв’язувати за схемою (див. рис. 1).

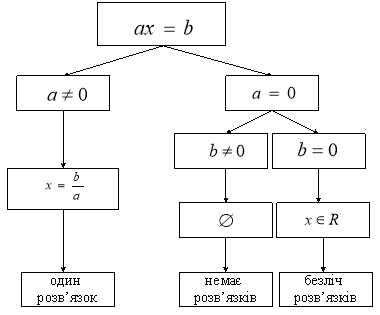
Рис. 1. Схема розв’язування лінійного рівняння з параметрами

Приклад 4. Розв’язати рівняння .

Неправильне розв’язання

Під час розв’язування даного рівняння учні отримують такі відповіді:

1) Відповідь: якщо , то або .

2) Відповідь: якщо , то або ; якщо , то .

Правильне розв’язання

1) ОДЗ .

.

2) Якщо , тоді , то або .

3) Якщо , то рівняння , але ОДЗ.

Відповідь: якщо , то або ; якщо , то розв’язків не має.

Приклад 5. При якому значенні рівняння має розв’язок?

Неправильне розв’язання

; , .

Правильне розв’язання

Для рівняння  єдиним розв’язком буде не тільки у випадку , як вирішує багато хто з учнів, а й у тому випадку, коли рівняння вироджується у лінійне, якщо .

Відповідь: або .

Щоб зменшити кількість помилок при розв’язанні квадратних рівнянь з параметрами корисно їх розв’язувати за схемами (див. рис. 2).

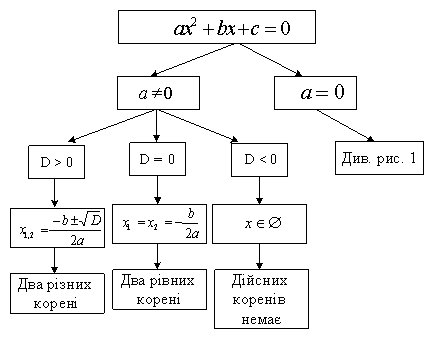
Рис. 2. Схема розв’язування квадратного рівняння з параметрами

На мою думку, наявність параметрів у рівняннях природно робить задачу більш складною, оскільки одночасно доводиться розв'язувати фактично необмежену кількість вправ, які виникають при фіксуванні різних значень параметрів. А це сприяє формуванню в учнів логічного мислення.