Презентація. "Системи лінійних рівнянь з двома змінними. Графічний метод розв'язування системи двох лінійних рівнянь із двома змінними"
Про матеріал
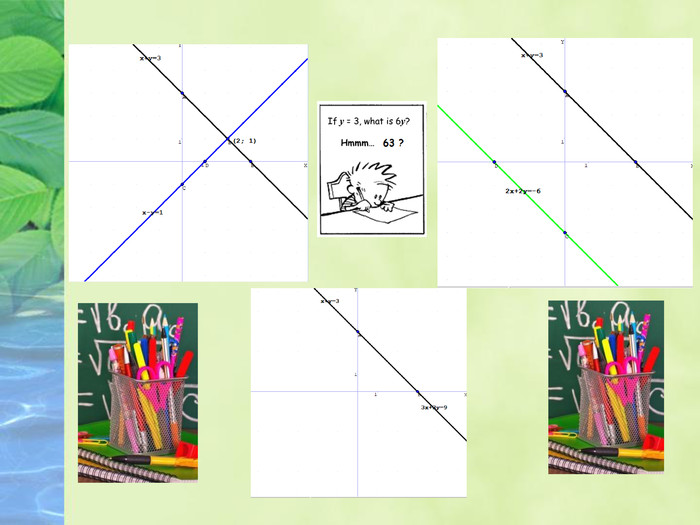
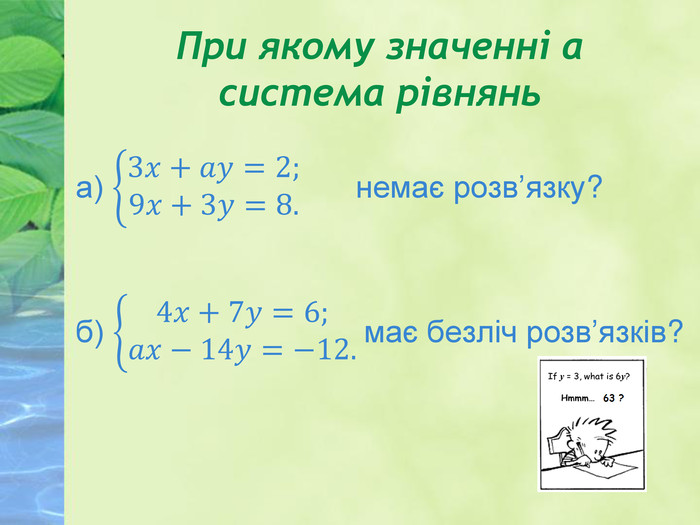
Другий урок з теми "Системи лінійних рівнянь з двома змінними" у 7 класі для дистанційного навчання. Презентація містить графічне розв'язування систем з урахуванням всіх можливих випадків розміщення графіків і відповідного висновку. Далі роз'яснюється, як визначити кількість розв'язків системи через коефіцієнти рівнянь, та відпрацьовується подана інформація через виконання вправ. Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку