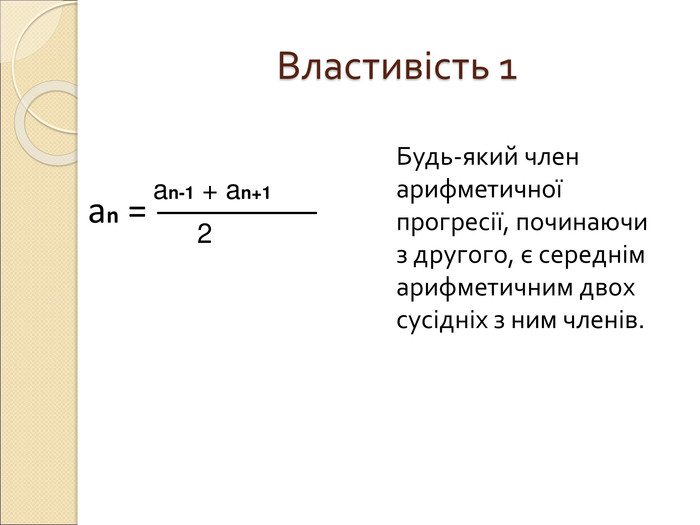
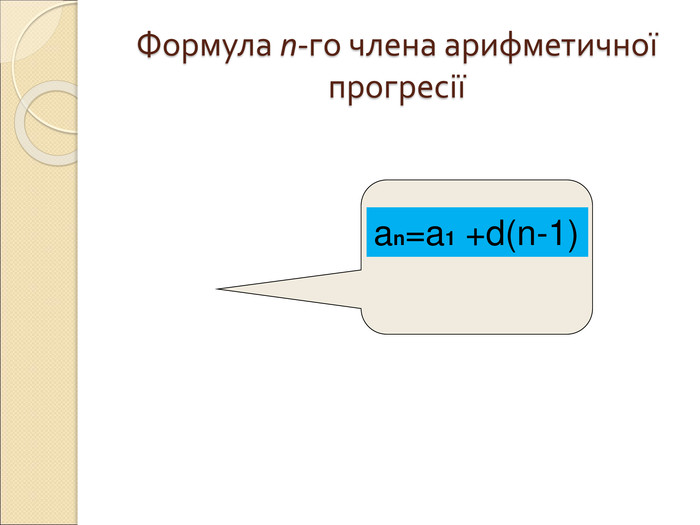
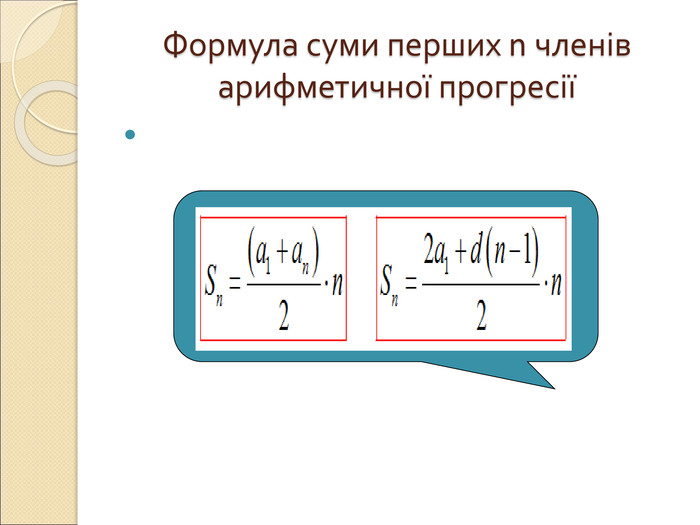
Арифметична прогресія.Презентація.
Про матеріал
Узагальнити знання учнів з теми «Арифметична прогресія»; активізувати взаємодію між учнями, актуалізувати досвід учнів, надати можливість “стати успішним”, закріпити навички обчислення елементів прогресії; провести контроль з метою встановлення рівня усвідомлення навчального матеріалу. Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку