Атестаційні завдання ДПА 9 клас
Збірка містить 10 варіантів атестаційних завдань на державну підсумкову атестацію з математики для 9 класу: 12 завдань у тестовій формі, 4 завдання на написання відповіді та 3 завдання з розгорнутою відповіддю.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 1
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
-
Знайдіть значення виразу
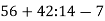 .
.
|
А |
Б |
В |
Г |
|
0 |
49 |
52 |
50 |
- Чому дорівнює найменше спільне кратне чисел 12 і 16?
|
А |
Б |
В |
Г |
|
48 |
2 |
96 |
4 |
- Яке з рівнянь є лінійним?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Яка пара чисел є розв’язком системи
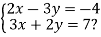
|
А |
Б |
В |
Г |
|
(2;1) |
(–1; –2) |
(–1;2) |
(1;2) |
-
Скоротіть дріб
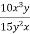 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Чому дорівнює сума коренів квадратного рівняння

|
А |
Б |
В |
Г |
|
9 |
5 |
–9 |
–5 |
-
Відомо, що
 . Яка з нерівностей хибна?
. Яка з нерівностей хибна?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Через яку з даних точок проходить графік рівняння
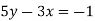 ?
?
|
А |
Б |
В |
Г |
|
(2;–1) |
(–2;1) |
(2;1) |
(–2; –1) |
- Скільки відрізків зображено на рисунку?
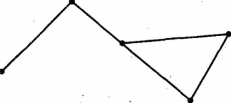 А) 5;
А) 5;
Б) 6;
В) 7;
Г) 4.
- У ромбі ABCD О – точка перетину діагоналей. Вкажіть вид трикутника АОD.
|
А |
Б |
В |
Г |
|
рівносторонній |
гострокутний |
тупокутний |
прямокутний |
-
Порівняйте катети АС і ВС прямокутного трикутника АВС, якщо
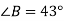 .
.
|
А |
Б |
В |
Г |
|
|
порівняти неможливо |
|
АС=ВС |
-
При якому значенні
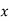 скалярний добуток векторів
скалярний добуток векторів 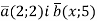 дорівнює 10?
дорівнює 10?
|
А |
Б |
В |
Г |
|
5 |
0 |
10 |
–5 |
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Знайдіть значення виразу
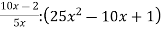 , якщо
, якщо 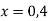 .
.
-
Один із коренів рівняння
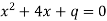 дорівнює –6. Знайти
дорівнює –6. Знайти  і другий корінь рівняння.
і другий корінь рівняння.
- Вкладник поклав до банку 10 000 грн. За перший рік йому нарахували 10% річних, а за другий рік – 12% річних. Який прибуток отримав вкладник через два роки?
- Сторони п’ятикутника відносяться як 2:3:4:5:6. Знайдіть найменшу сторону подібного йому п’ятикутника, якщо його периметр дорівнює 80 см.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Моторний човен пройшов 24 км проти течії річки і 18 км за течією, витративши на весь шлях 3 год. Знайдіть швидкість човна в стоячій воді, якщо швидкість течії річки становить 3 км/год.
-
Побудуйте графік функції
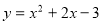 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- Діагональ рівнобічної трапеції з основами 25 см і 39 см є бісектрисою гострого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 2
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
-
Яке з чисел 3, 12, 14 є коренем рівняння
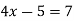 .
.
|
А |
Б |
В |
Г |
|
3 |
12 |
14 |
жодне |
-
Виконайте множення
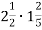 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яку цифру із запропонованих можна поставити замість зірочки у запис 365*, щоб отримане число було кратним числу 3?
|
А |
Б |
В |
Г |
|
3 |
6 |
9 |
1 |
-
Спростіть вираз
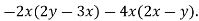
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Графік функції
 перенесли на 2 одиниці вгору. Графік якої функції було отримано?
перенесли на 2 одиниці вгору. Графік якої функції було отримано?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Виконайте ділення
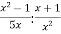 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Для якої з нерівностей число 1 є розв’язком?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайти різницю арифметичної прогресії
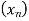 , якщо
, якщо 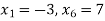 .
.
|
А |
Б |
В |
Г |
|
|
10 |
2 |
4 |
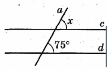
-
Якої градусної міри має бути кут
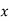 , щоб прямі
, щоб прямі 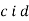 паралельні?
паралельні?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Прямі MN i PK паралельні. Відрізки PN i KM перетинаються в точці О, при цьому
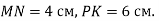 Знайти відношення NO:OP.
Знайти відношення NO:OP.
|
А |
Б |
В |
Г |
|
2:3 |
1:2 |
1:3 |
3:2 |
-
Обчислити площу трикутника, дві сторони якого дорівнюють 3 см і 2 см, а кут між ними дорівнює
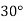 .
.
|
А |
Б |
В |
Г |
|
|
3 |
|
|
-
Площа гострокутного трикутника АВС дорівнює
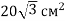 . Знайдіть кут В трикутника, якщо АВ = 8 см, ВС = 10 см.
. Знайдіть кут В трикутника, якщо АВ = 8 см, ВС = 10 см.
|
А |
Б |
В |
Г |
|
|
|
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Знайдіть значення виразу
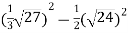 .
.
-
Один з коренів рівняння
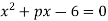 дорівнює 1,5. Знайдіть р і другий корінь рівняння.
дорівнює 1,5. Знайдіть р і другий корінь рівняння.
- У сплаві 60% міді, а решта – 200г – олово. Яка маса сплаву?
- Сторони трикутника відносяться як 3: 4: 5. Знайдіть найбільшу сторону подібного йому трикутника, якщо його периметр дорівнює 36см.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Відстань між двома містами по річці дорівнює 30 км. Моторний човен пройшов цей шлях у два кінці за 10 год. Знайдіть швидкість човна у стоячій воді, якщо швидкість течії річки становить 4 км/год.
-
Побудуйте графік функції
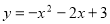 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- Діагональ рівнобічної трапеції з основами 11 см і 25 см є бісектрисою тупого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 3
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
- Знайдіть різницю 16 год 26 хв – 9 год 52 хв.
|
А |
Б |
В |
Г |
|
6 год 26 хв |
7 год 34 хв |
6 год 34 хв |
7 год 26 хв |
-
Знайдіть суму
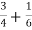 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Який із виразів є одночленом?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
При якому значенні
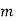 значення виразу
значення виразу 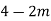 дорівнює 7?
дорівнює 7?
|
А |
Б |
В |
Г |
|
–1,5 |
–10 |
1,5 |
–5,5 |
-
Виконайте ділення
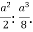
|
А |
Б |
В |
Г |
|
|
|
|
|
-
При якому значенні змінної
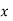 дріб
дріб 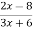 не має змісту?
не має змісту?
|
А |
Б |
В |
Г |
|
2 |
–2,4 |
–2 |
–4 |
- Яка з поданих послідовностей є геометричною прогресією?
|
А |
Б |
В |
Г |
|
5, 10, 20, 50… |
2, 8, 32, 128… |
3, 9, 27, 30… |
2, 8, 12, 16… |
- Яка ймовірність того, що при одному підкиданні грального кубика випаде кількість очок, до дорівнює парному числу?
|
А |
Б |
В |
Г |
|
|
|
|
1 |
-
Бісектриса кута А утворює з його стороною кут
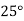 . Знайдіть градусну міру кута, суміжного з кутом А.
. Знайдіть градусну міру кута, суміжного з кутом А.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Кути рівнобічної трапеції можуть дорівнювати…
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть координати вектора
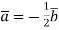 , якщо
, якщо 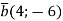 .
.
|
А |
Б |
В |
Г |
|
(–2;–3) |
(2;3) |
(–2;3) |
(2;–3) |
- Складіть рівняння кола з центром у точці М (–3;1), яке проходить через точку К(–1;5).
|
А |
Б |
В |
Г |
|
|
|
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Розв’яжіть рівняння
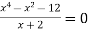 .
.
-
На прямій
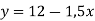 знайдіть точку, абсциса якої удвічі більша за ординату.
знайдіть точку, абсциса якої удвічі більша за ординату.
-
Знайдіть суму двадцяти перших членів арифметичної прогресії
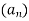 , якщо
, якщо 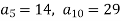 .
.
-
У прямокутній трапеції гострий кут дорівнює
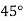 , менша бічна сторона і менша основа трапеції – по 6 см. Знайдіть середню лінію трапеції.
, менша бічна сторона і менша основа трапеції – по 6 см. Знайдіть середню лінію трапеції.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Моторний човен пройшов за течією річки 28 км і відразу повернувся назад, витративши на весь шлях 7 год. Знайдіть швидкість човна в стоячій воді, якщо швидкість течії річки становить 3 км/год.
-
Побудуйте графік функції
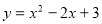 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- У прямокутній трапеції бічні сторони дорівнюють 24 см і 25 см, а більша діагональ є бісектрисою гострого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 4
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
-
Спростіть вираз
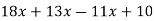 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть відсоткове відношення 0,2 до
 .
.
|
А |
Б |
В |
Г |
|
6,25% |
16% |
62,5% |
1,6% |
-
Знайдіть ширину прямокутника, довжина якого 7 см, ширина –
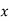 см, а периметр 25 см. Яке з наведених рівнянь відповідає умові задачі?
см, а периметр 25 см. Яке з наведених рівнянь відповідає умові задачі?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Спростіть вираз
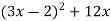 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Серед наведених чисел укажіть ірраціональне число.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Скоротіть дріб
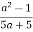 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
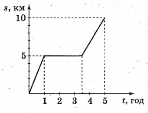
- На рисунку показано графік руху туриста. Скільки часу тривав привал?
|
А |
Б |
В |
Г |
|
1год |
2,5 год |
3,5 год |
5 год |
-
Розв’яжіть нерівність
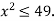
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть кут при вершині рівнобедреного трикутника, якщо кут при основі дорівнює
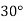 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Обчисліть площу трапеції, у якої сума основ дорівнює 20 см, а висота – 6 см.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть модуль вектора
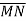 , якщо
, якщо 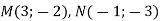 .
.
|
А |
Б |
В |
Г |
|
|
|
29 |
17 |
-
При якому значенні
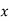 вектори
вектори 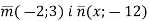 колінеарні?
колінеарні?
|
А |
Б |
В |
Г |
|
|
|
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Розв’яжіть рівняння
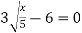 .
.
-
При яких значеннях
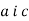 нулями функції
нулями функції 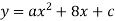 є числа –6 і 2?
є числа –6 і 2?
-
Спростіть вираз
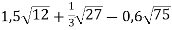 .
.
-
При якому значенні
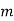 вектори
вектори 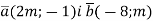 колінеарні?
колінеарні?
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Теплохід за 2 год пройшов 30 км озером і 12 км за течією річки. Знайдіть швидкість руху теплохода по озеру, якщо швидкість течії річки становить 4 км/год.
-
Побудуйте графік функції
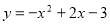 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- У прямокутній трапеції бічні сторони дорівнюють 35 см і 37 см, а менша діагональ є бісектрисою тупого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 5
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
- Запишіть десятковий дріб 3,07 у вигляді мішаного числа.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Обчисліть значення виразу
 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Укажіть пару чисел, яка є розв’язком рівняння
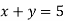 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть значення змінної
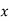 ,при якому значення виразів
,при якому значення виразів 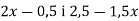 рівні.
рівні.
|
А |
Б |
В |
Г |
|
4 |
|
–4 |
|
-
Знайдіть корені квадратного рівняння
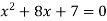 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Виконайте додавання
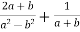 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Знайдіть різницю арифметичної прогресії 8; 3;–2; – 7…
|
А |
Б |
В |
Г |
|
5 |
–5 |
8 |
3 |
- В урні знаходиться 35 куль, пронумерованих від 1 до 35. З цієї урни навмання виймають одну кулю. Знайдіть ймовірність того, що номер кулі виявиться таким, у записі якого є цифра 3.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Скільки спільних точок має пряма з колом, діаметр якого дорівнює 8 см, якщо пряма розміщена на відстані 4 см від центра кола?
|
А |
Б |
В |
Г |
|
Одну |
Дві |
Жодної |
Три |
-
У прямокутному рівнобедреному трикутнику гіпотенуза дорівнює
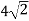 см. Знайдіть катет.
см. Знайдіть катет.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть координати вектора
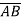 , якщо
, якщо 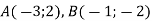 .
.
|
А |
Б |
В |
Г |
|
(–4;0) |
(–2;–4) |
(2;–4) |
(4;0) |
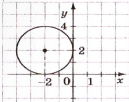
1.12. Складіть рівняння кола, зображеного на рисунку.
|
А |
Б |
В |
Г |
|
|
|
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Подайте у вигляді дробу вираз
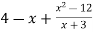 .
.
-
Знайдіть найменше ціле число, що є розв’язком нерівності:
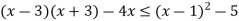 .
.
-
Винесіть множник з-під знака кореня у виразі
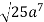 .
.
-
Відстань між точками
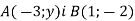 дорівнює 5. Знайдіть
дорівнює 5. Знайдіть 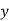 .
.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Катер проплив 45 км за течією річки і 12 км по озеру, затративши на весь шлях 3 год. Знайдіть власну швидкість катера, якщо швидкість течії річки становить 4 км ̸ год.
-
Побудуйте графік функції
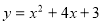 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- У прямокутній трапеції бічні сторони дорівнюють 36 см і 39 см, а більша діагональ є бісектрисою прямого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 6
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
-
Знайдіть значення виразу
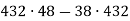 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яке число є дільником числа 12?
|
А |
Б |
В |
Г |
|
5 |
– 5 |
8 |
3 |
- Яке з рівнянь не має коренів?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Розкладіть на множники многочлен
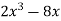 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Виконайте додавання
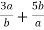 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Скільки коренів має квадратне рівняння
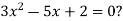
|
А |
Б |
В |
Г |
|
Два |
Один |
Жодного |
Безліч |
-
Оцініть значення виразу
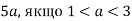 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть перший член арифметичної прогресії
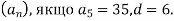
|
А |
Б |
В |
Г |
|
10 |
11 |
5 |
15 |
- На якій відстані від кінців відрізка завдовжки 70 см лежить точка, яка поділяє його на дві частини у відношенні 5:2?
|
А |
Б |
В |
Г |
|
56 см; 14 см |
14 см; 56 см |
50 см; 20 см |
50 см; 70 см |
-
У ромбі
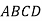 кут
кут 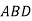 дорівнює
дорівнює 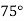 .Чому дорівнює
.Чому дорівнює 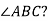
|
А |
Б |
В |
Г |
|
|
|
|
|
-
У рівнобедреному трикутнику основа дорівнює
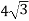 см, а медіана, проведена до неї,
см, а медіана, проведена до неї, 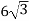 см. Знайдіть площу трикутника.
см. Знайдіть площу трикутника.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Який із векторів колінеарний вектору
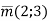 ?
?
|
А |
Б |
В |
Г |
|
|
|
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Розв’яжіть рівняння
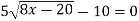 .
.
-
Графіку функції
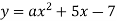 належить точка
належить точка 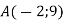 . Знайдіть коефіцієнт
. Знайдіть коефіцієнт 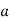 .
.
-
Розв’яжіть систему рівнянь
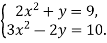
- Катет прямокутного трикутника відноситься до гіпотенузи як 5:13. Знайдіть периметр трикутника, якщо його другий катет дорівнює 24 см.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Моторний човен пройшов 20 км за течією річки і 32 км озером, затративши на весь шлях 4 год. Швидкість течії річки дорівнює 3 км/год. Знайдіть швидкість човна за течією річки.
-
Побудуйте графік функції
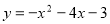 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- У прямокутній трапеції бічні сторони дорівнюють 24 см і 26 см, а менша діагональ є бісектрисою прямого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 7
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
- Запишіть 3 год 24 хв у хвилинах.
|
А |
Б |
В |
Г |
|
27 хв |
324 хв |
204 хв |
54 хв |
-
Чому дорівнює значення виразу
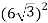 ?
?
|
А |
Б |
В |
Г |
|
18 |
36 |
54 |
108 |
- Укажіть хибне твердження:
|
А |
Б |
В |
Г |
|
–3 – ціле число |
–3 – недодатне число |
–3 – раціональне число |
–3 – невід’ємне число |
-
Знайдіть нулі функції
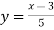 .
.
|
А |
Б |
В |
Г |
|
5 |
3 |
5 і 3 |
–3 |
-
Виконайте множення
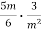 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Внесіть множник під знак кореня
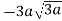 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
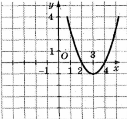
1.7. На рисунку зображено графік функції ![]() . Вкажіть проміжок спадання функції.
. Вкажіть проміжок спадання функції.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Вкладник поклав до банку 1500 грн. Під який відсоток річних покладено гроші, якщо через рік на рахунку вкладника було 1725 грн.?
|
А |
Б |
В |
Г |
|
115% |
85% |
15% |
25% |
-
Який кут вертикальний з
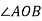 ?
?
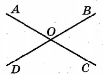
|
А |
Б |
В |
Г |
|
|
|
|
|
- Знайдіть меншу основу рівнобічної трапеції, якщо висота, проведена з вершини тупого кута, ділить більшу основу на відрізки 4 дм і 16 дм.
|
А |
Б |
В |
Г |
|
10 дм |
12 дм |
16 дм |
8 дм |
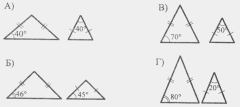
1.11. На якому рисунку зображені рівнобедрені трикутники є подібними?
1.12. Відстань від точки А (1;2) до точки ![]() дорівнює 5. Знайдіть значення
дорівнює 5. Знайдіть значення ![]() .
.
|
А |
Б |
В |
Г |
|
–6; 2 |
–2 |
6 |
–2; 6 |
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
- Підприємець поклав у банк 50 000 грн. під 10% річних. Яка сума буде у нього на рахунку через 2 роки?
-
Знайдіть координати точок перетину прямої
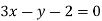 і параболи
і параболи 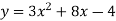 .
.
-
Знайдіть знаменник геометричної прогресії
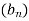 , у якої
, у якої 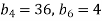 .
.
- Один із катетів прямокутного трикутника дорівнює 12 см, а інший – на 8 см менший за гіпотенузу. Знайдіть периметр трикутника.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Моторний човен пройшов 40 км проти течії річки і 28 км озером, затративши на шлях по озеру на 2 год менше, ніж на шлях по річці. Швидкість течії річки дорівнює 4 км/год. Знайдіть швидкість човна проти течії річки.
-
Побудуйте графік функції
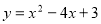 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- У прямокутній трапеції бічні сторони дорівнюють 36 см і 39 см, а більша діагональ є бісектрисою прямого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 8
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
- Яка числова нерівність є правильною?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Виконайте ділення
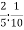 .
.
|
А |
Б |
В |
Г |
|
|
25 |
4 |
|
-
Скільки коренів має рівняння
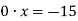 ?
?
|
А |
Б |
В |
Г |
|
безліч |
один |
жодного |
два |
-
Спростіть вираз
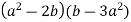 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Розв’язком якого рівняння є пара чисел
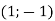 ?
?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Виконайте множення
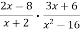 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
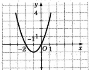 На рисунку зображено графік функції
На рисунку зображено графік функції 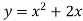 . Знайдіть множину розв’язків нерівності
. Знайдіть множину розв’язків нерівності 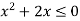 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Протягом восьмигодинного робочого дня робітник щогодини виготовляє 12; 10; 8; 11; 9; 12; 10; 8 деталей. Знайдіть середнє значення даної вибірки.
|
А |
Б |
В |
Г |
|
11 |
9 |
10 |
12 |
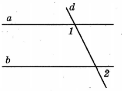
-
На рисунку зображено паралельні прямі
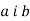 , які перетинає січна
, які перетинає січна 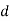 . Користуючись рисунком, знайдіть
. Користуючись рисунком, знайдіть 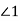 , якщо
, якщо 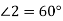 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Один з кутів паралелограма дорівнює
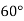 . Знайдіть решту його кутів.
. Знайдіть решту його кутів.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
У трикутнику
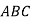
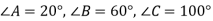 . Яка сторона трикутника є найбільшою?
. Яка сторона трикутника є найбільшою?
|
А |
Б |
В |
Г |
|
АС |
ВС |
Неможливо визначити |
АВ |
-
При якому значенні
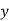 вектори
вектори 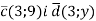 перпендикулярні?
перпендикулярні?
|
А |
Б |
В |
Г |
|
1 |
9 |
–1 |
3 |
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Розв’яжіть рівняння
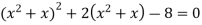 .
.
-
Розв’яжіть нерівність
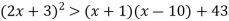 .
.
- Із натуральних чисел від 1 до 24 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 24?
-
У паралелограмі
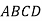 бісектриса кута А ділить сторону ВС на відрізки
бісектриса кута А ділить сторону ВС на відрізки 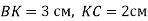 . Знайдіть периметр паралелограма.
. Знайдіть периметр паралелограма.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Катер проплив 24 км за течією річки і 48 км проти течії, витративши на весь шлях 4 год. Знайдіть швидкість катера за течією, якщо власна швидкість катера дорівнює 20 км ̸ год.
-
Побудуйте графік функції
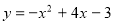 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- Діагональ рівнобічної трапеції з основами 25 см і 39 см є бісектрисою гострого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 9
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
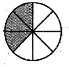
- Яку частину круга на рисунку заштриховано?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Подайте у вигляді степеня вираз
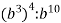 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть значення аргументу, при якому функція
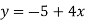 має значення 3.
має значення 3.
|
А |
Б |
В |
Г |
|
|
2 |
7 |
|
-
Спростіть вираз
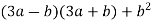 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Між якими двома послідовними натуральними числами міститься на координатній прямій число
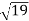 ?
?
|
А |
Б |
В |
Г |
|
3 і 4 |
4 і 5 |
5 і 6 |
6 і 7 |
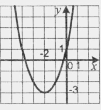
1.6. На рисунку зображено графік функції ![]() . Вкажіть проміжок спадання функції.
. Вкажіть проміжок спадання функції.
|
А |
Б |
В |
Г |
|
|
|
|
|
1.7. Яку суму отримає вкладник через рік, якщо він поклав до банку 5000 грн. під 15% річних?
|
А |
Б |
В |
Г |
|
5750 грн. |
5015 грн. |
5075 грн. |
750 грн. |
-
Розв’яжіть нерівність
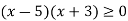 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
1.9. Визначте вид трикутника ![]() , якщо
, якщо ![]() .
.
|
А |
Б |
В |
Г |
|
гострокутний |
прямокутний |
Визначити неможливо |
тупокутний |
- Сторони трикутника відносяться як 7: 6: 4. Знайдіть більшу сторону подібного йому трикутника, менша сторона якого дорівнює 12 см.
|
А |
Б |
В |
Г |
|
84 см |
56 см |
14 см |
21 см |
- Точка М – середина відрізка АВ. Знайдіть координати точки М, якщо А(2; –3), В(–6; 7).
|
А |
Б |
В |
Г |
|
(4; –5) |
(–2; 2) |
(2; –2) |
(–4; 4) |
-
Обчисліть модуль вектора
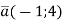 .
.
|
А |
Б |
В |
Г |
|
3 |
5 |
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Знайдіть значення виразу
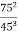 .
.
-
Знайдіть суму десяти перших членів арифметичної прогресії
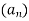 , якщо
, якщо  ,
, 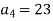 .
.
-
Скільки цілих чисел містить множина розв’язків нерівності
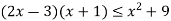 ?
?
-
У прямокутній трапеції гострий кут дорівнює
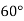 . Більша бічна сторона і більша основа дорівнюють по 12 см. Знайдіть середню лінію трапеції.
. Більша бічна сторона і більша основа дорівнюють по 12 см. Знайдіть середню лінію трапеції.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Моторний човен пройшов 28 км за течією річки і 40 км проти течії, затративши на шлях за течією на 2 год менше, ніж на шлях проти течії . Власна швидкість човна дорівнює 12 км/год. Знайдіть швидкість човна проти течії річки.
-
Побудуйте графік функції
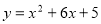 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- Діагональ рівнобічної трапеції ділить середню лінію на відрізки 13 см і 23 см. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 10
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
-
Подайте у вигляді степеня вираз
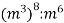 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яка із числових нерівностей є правильною?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть розв’язок системи рівнянь
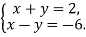
|
А |
Б |
В |
Г |
|
|
|
|
|
1.4. Розв’яжіть рівняння ![]() .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Укажіть многочлен, який тотожно дорівнює виразу
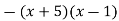 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
1.6. Виконайте віднімання ![]() .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
1.7. Знайдіть знаменник геометричної прогресії 6; –2; ![]() .
.
|
А |
Б |
В |
Г |
|
|
|
3 |
–3 |
-
Оцініть значення виразу
 якщо
якщо 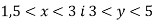 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
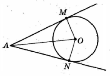 На рисунку
На рисунку 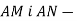 дотичні до кола з центром у точці О. Відомо, що
дотичні до кола з центром у точці О. Відомо, що 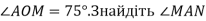 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють
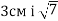 см.
см.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
У трикутнику АВС
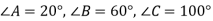 . Яка сторона трикутника є найбільшою?
. Яка сторона трикутника є найбільшою?
|
А |
Б |
В |
Г |
|
АС |
ВС |
Визначити неможливо |
АВ |
-
Обчисліть модуль вектора
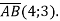
|
А |
Б |
В |
Г |
|
7 |
1 |
5 |
25 |
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
При яких значеннях
 рівняння
рівняння  не має коренів?
не має коренів?
-
Розв’яжіть систему рівнянь
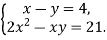
-
Число –2 є коренем рівняння
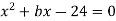 . Знайдіть другий корінь і число
. Знайдіть другий корінь і число 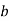 .
.
- Сторони трикутника відносяться як 6:7:8. Знайдіть периметр подібного йому трикутника, середня за довжиною сторона якого дорівнює 21 см.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Човен пропливає 9 км за течією річки і 1 км проти течії за такий самий час, який потрібен плоту, щоб проплисти 4 км по цій річці. Знайдіть швидкість течії, якщо власна швидкість човна становить 8 км/год.
-
Побудуйте графік функції
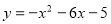 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- Діагональ рівнобічної трапеції ділить середню лінію на відрізки 3 см і 13 см. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 11
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
-
Знайдіть значення виразу
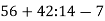 .
.
|
А |
Б |
В |
Г |
|
0 |
49 |
52 |
50 |
- Чому дорівнює найменше спільне кратне чисел 12 і 16?
|
А |
Б |
В |
Г |
|
48 |
2 |
96 |
4 |
- Яке з рівнянь є лінійним?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Яка пара чисел є розв’язком системи
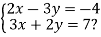
|
А |
Б |
В |
Г |
|
(2;1) |
(–1; –2) |
(–1;2) |
(1;2) |
-
Скоротіть дріб
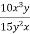 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Чому дорівнює сума коренів квадратного рівняння

|
А |
Б |
В |
Г |
|
9 |
5 |
–9 |
–5 |
-
Відомо, що
 . Яка з нерівностей хибна?
. Яка з нерівностей хибна?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Через яку з даних точок проходить графік рівняння
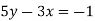 ?
?
|
А |
Б |
В |
Г |
|
(2;–1) |
(–2;1) |
(2;1) |
(–2; –1) |
- Скільки відрізків зображено на рисунку?
 А) 5;
А) 5;
Б) 6;
В) 7;
Г) 4.
- У ромбі ABCD О – точка перетину діагоналей. Вкажіть вид трикутника АОD.
|
А |
Б |
В |
Г |
|
рівносторонній |
гострокутний |
тупокутний |
прямокутний |
-
Порівняйте катети АС і ВС прямокутного трикутника АВС, якщо
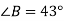 .
.
|
А |
Б |
В |
Г |
|
|
порівняти неможливо |
|
АС=ВС |
-
При якому значенні
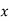 скалярний добуток векторів
скалярний добуток векторів 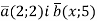 дорівнює 10?
дорівнює 10?
|
А |
Б |
В |
Г |
|
5 |
0 |
10 |
–5 |
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Знайдіть значення виразу
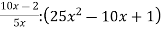 , якщо
, якщо 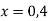 .
.
-
Один із коренів рівняння
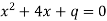 дорівнює –6. Знайти
дорівнює –6. Знайти  і другий корінь рівняння.
і другий корінь рівняння.
- Вкладник поклав до банку 10 000 грн. За перший рік йому нарахували 10% річних, а за другий рік – 12% річних. Який прибуток отримав вкладник через два роки?
- Сторони п’ятикутника відносяться як 2:3:4:5:6. Знайдіть найменшу сторону подібного йому п’ятикутника, якщо його периметр дорівнює 80 см.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Моторний човен пройшов 24 км проти течії річки і 18 км за течією, витративши на весь шлях 3 год. Знайдіть швидкість човна в стоячій воді, якщо швидкість течії річки становить 3 км/год.
-
Побудуйте графік функції
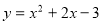 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- Діагональ рівнобічної трапеції з основами 25 см і 39 см є бісектрисою гострого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 12
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
-
Яке з чисел 3, 12, 14 є коренем рівняння
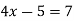 .
.
|
А |
Б |
В |
Г |
|
3 |
12 |
14 |
жодне |
-
Виконайте множення
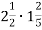 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яку цифру із запропонованих можна поставити замість зірочки у запис 365*, щоб отримане число було кратним числу 3?
|
А |
Б |
В |
Г |
|
3 |
6 |
9 |
1 |
-
Спростіть вираз
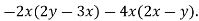
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Графік функції
 перенесли на 2 одиниці вгору. Графік якої функції було отримано?
перенесли на 2 одиниці вгору. Графік якої функції було отримано?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Виконайте ділення
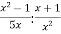 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Для якої з нерівностей число 1 є розв’язком?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайти різницю арифметичної прогресії
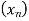 , якщо
, якщо 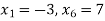 .
.
|
А |
Б |
В |
Г |
|
|
10 |
2 |
4 |

-
Якої градусної міри має бути кут
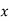 , щоб прямі
, щоб прямі 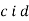 паралельні?
паралельні?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Прямі MN i PK паралельні. Відрізки PN i KM перетинаються в точці О, при цьому
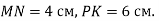 Знайти відношення NO:OP.
Знайти відношення NO:OP.
|
А |
Б |
В |
Г |
|
2:3 |
1:2 |
1:3 |
3:2 |
-
Обчислити площу трикутника, дві сторони якого дорівнюють 3 см і 2 см, а кут між ними дорівнює
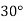 .
.
|
А |
Б |
В |
Г |
|
|
3 |
|
|
-
Площа гострокутного трикутника АВС дорівнює
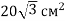 . Знайдіть кут В трикутника, якщо АВ = 8 см, ВС = 10 см.
. Знайдіть кут В трикутника, якщо АВ = 8 см, ВС = 10 см.
|
А |
Б |
В |
Г |
|
|
|
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Знайдіть значення виразу
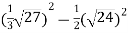 .
.
-
Один з коренів рівняння
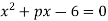 дорівнює 1,5. Знайдіть р і другий корінь рівняння.
дорівнює 1,5. Знайдіть р і другий корінь рівняння.
- У сплаві 60% міді, а решта – 200г – олово. Яка маса сплаву?
- Сторони трикутника відносяться як 3: 4: 5. Знайдіть найбільшу сторону подібного йому трикутника, якщо його периметр дорівнює 36см.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Відстань між двома містами по річці дорівнює 30 км. Моторний човен пройшов цей шлях у два кінці за 10 год. Знайдіть швидкість човна у стоячій воді, якщо швидкість течії річки становить 4 км/год.
-
Побудуйте графік функції
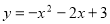 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- Діагональ рівнобічної трапеції з основами 11 см і 25 см є бісектрисою тупого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 13
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
- Знайдіть різницю 16 год 26 хв – 9 год 52 хв.
|
А |
Б |
В |
Г |
|
6 год 26 хв |
7 год 34 хв |
6 год 34 хв |
7 год 26 хв |
-
Знайдіть суму
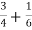 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Який із виразів є одночленом?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
При якому значенні
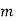 значення виразу
значення виразу 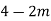 дорівнює 7?
дорівнює 7?
|
А |
Б |
В |
Г |
|
–1,5 |
–10 |
1,5 |
–5,5 |
-
Виконайте ділення
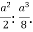
|
А |
Б |
В |
Г |
|
|
|
|
|
-
При якому значенні змінної
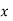 дріб
дріб 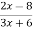 не має змісту?
не має змісту?
|
А |
Б |
В |
Г |
|
2 |
–2,4 |
–2 |
–4 |
- Яка з поданих послідовностей є геометричною прогресією?
|
А |
Б |
В |
Г |
|
5, 10, 20, 50… |
2, 8, 32, 128… |
3, 9, 27, 30… |
2, 8, 12, 16… |
- Яка ймовірність того, що при одному підкиданні грального кубика випаде кількість очок, до дорівнює парному числу?
|
А |
Б |
В |
Г |
|
|
|
|
1 |
-
Бісектриса кута А утворює з його стороною кут
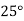 . Знайдіть градусну міру кута, суміжного з кутом А.
. Знайдіть градусну міру кута, суміжного з кутом А.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Кути рівнобічної трапеції можуть дорівнювати…
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть координати вектора
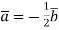 , якщо
, якщо 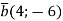 .
.
|
А |
Б |
В |
Г |
|
(–2;–3) |
(2;3) |
(–2;3) |
(2;–3) |
- Складіть рівняння кола з центром у точці М (–3;1), яке проходить через точку К(–1;5).
|
А |
Б |
В |
Г |
|
|
|
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Розв’яжіть рівняння
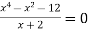 .
.
-
На прямій
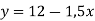 знайдіть точку, абсциса якої удвічі більша за ординату.
знайдіть точку, абсциса якої удвічі більша за ординату.
-
Знайдіть суму двадцяти перших членів арифметичної прогресії
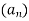 , якщо
, якщо 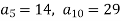 .
.
-
У прямокутній трапеції гострий кут дорівнює
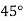 , менша бічна сторона і менша основа трапеції – по 6 см. Знайдіть середню лінію трапеції.
, менша бічна сторона і менша основа трапеції – по 6 см. Знайдіть середню лінію трапеції.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Моторний човен пройшов за течією річки 28 км і відразу повернувся назад, витративши на весь шлях 7 год. Знайдіть швидкість човна в стоячій воді, якщо швидкість течії річки становить 3 км/год.
-
Побудуйте графік функції
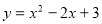 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- У прямокутній трапеції бічні сторони дорівнюють 24 см і 25 см, а більша діагональ є бісектрисою гострого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 14
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
-
Спростіть вираз
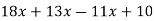 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть відсоткове відношення 0,2 до
 .
.
|
А |
Б |
В |
Г |
|
6,25% |
16% |
62,5% |
1,6% |
-
Знайдіть ширину прямокутника, довжина якого 7 см, ширина –
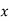 см, а периметр 25 см. Яке з наведених рівнянь відповідає умові задачі?
см, а периметр 25 см. Яке з наведених рівнянь відповідає умові задачі?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Спростіть вираз
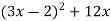 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Серед наведених чисел укажіть ірраціональне число.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Скоротіть дріб
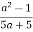 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|

- На рисунку показано графік руху туриста. Скільки часу тривав привал?
|
А |
Б |
В |
Г |
|
1год |
2,5 год |
3,5 год |
5 год |
-
Розв’яжіть нерівність
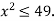
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть кут при вершині рівнобедреного трикутника, якщо кут при основі дорівнює
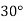 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Обчисліть площу трапеції, у якої сума основ дорівнює 20 см, а висота – 6 см.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть модуль вектора
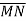 , якщо
, якщо 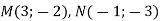 .
.
|
А |
Б |
В |
Г |
|
|
|
29 |
17 |
-
При якому значенні
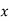 вектори
вектори 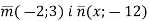 колінеарні?
колінеарні?
|
А |
Б |
В |
Г |
|
|
|
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Розв’яжіть рівняння
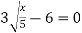 .
.
-
При яких значеннях
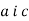 нулями функції
нулями функції 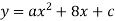 є числа –6 і 2?
є числа –6 і 2?
-
Спростіть вираз
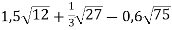 .
.
-
При якому значенні
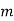 вектори
вектори 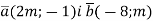 колінеарні?
колінеарні?
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Теплохід за 2 год пройшов 30 км озером і 12 км за течією річки. Знайдіть швидкість руху теплохода по озеру, якщо швидкість течії річки становить 4 км/год.
-
Побудуйте графік функції
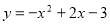 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- У прямокутній трапеції бічні сторони дорівнюють 35 см і 37 см, а менша діагональ є бісектрисою тупого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 15
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
- Запишіть десятковий дріб 3,07 у вигляді мішаного числа.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Обчисліть значення виразу
 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Укажіть пару чисел, яка є розв’язком рівняння
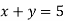 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть значення змінної
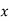 ,при якому значення виразів
,при якому значення виразів 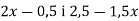 рівні.
рівні.
|
А |
Б |
В |
Г |
|
4 |
|
–4 |
|
-
Знайдіть корені квадратного рівняння
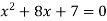 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Виконайте додавання
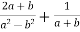 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Знайдіть різницю арифметичної прогресії 8; 3;–2; – 7…
|
А |
Б |
В |
Г |
|
5 |
–5 |
8 |
3 |
- В урні знаходиться 35 куль, пронумерованих від 1 до 35. З цієї урни навмання виймають одну кулю. Знайдіть ймовірність того, що номер кулі виявиться таким, у записі якого є цифра 3.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Скільки спільних точок має пряма з колом, діаметр якого дорівнює 8 см, якщо пряма розміщена на відстані 4 см від центра кола?
|
А |
Б |
В |
Г |
|
Одну |
Дві |
Жодної |
Три |
-
У прямокутному рівнобедреному трикутнику гіпотенуза дорівнює
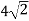 см. Знайдіть катет.
см. Знайдіть катет.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть координати вектора
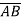 , якщо
, якщо 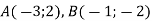 .
.
|
А |
Б |
В |
Г |
|
(–4;0) |
(–2;–4) |
(2;–4) |
(4;0) |

1.12. Складіть рівняння кола, зображеного на рисунку.
|
А |
Б |
В |
Г |
|
|
|
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Подайте у вигляді дробу вираз
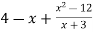 .
.
-
Знайдіть найменше ціле число, що є розв’язком нерівності:
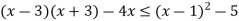 .
.
-
Винесіть множник з-під знака кореня у виразі
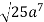 .
.
-
Відстань між точками
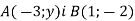 дорівнює 5. Знайдіть
дорівнює 5. Знайдіть 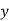 .
.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Катер проплив 45 км за течією річки і 12 км по озеру, затративши на весь шлях 3 год. Знайдіть власну швидкість катера, якщо швидкість течії річки становить 4 км ̸ год.
-
Побудуйте графік функції
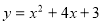 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- У прямокутній трапеції бічні сторони дорівнюють 36 см і 39 см, а більша діагональ є бісектрисою прямого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 16
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
-
Знайдіть значення виразу
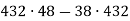 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яке число є дільником числа 12?
|
А |
Б |
В |
Г |
|
5 |
– 5 |
8 |
3 |
- Яке з рівнянь не має коренів?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Розкладіть на множники многочлен
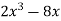 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Виконайте додавання
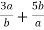 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Скільки коренів має квадратне рівняння
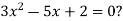
|
А |
Б |
В |
Г |
|
Два |
Один |
Жодного |
Безліч |
-
Оцініть значення виразу
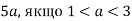 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть перший член арифметичної прогресії
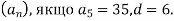
|
А |
Б |
В |
Г |
|
10 |
11 |
5 |
15 |
- На якій відстані від кінців відрізка завдовжки 70 см лежить точка, яка поділяє його на дві частини у відношенні 5:2?
|
А |
Б |
В |
Г |
|
56 см; 14 см |
14 см; 56 см |
50 см; 20 см |
50 см; 70 см |
-
У ромбі
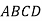 кут
кут 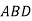 дорівнює
дорівнює 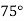 .Чому дорівнює
.Чому дорівнює 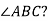
|
А |
Б |
В |
Г |
|
|
|
|
|
-
У рівнобедреному трикутнику основа дорівнює
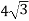 см, а медіана, проведена до неї,
см, а медіана, проведена до неї, 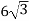 см. Знайдіть площу трикутника.
см. Знайдіть площу трикутника.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Який із векторів колінеарний вектору
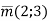 ?
?
|
А |
Б |
В |
Г |
|
|
|
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Розв’яжіть рівняння
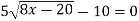 .
.
-
Графіку функції
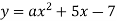 належить точка
належить точка 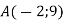 . Знайдіть коефіцієнт
. Знайдіть коефіцієнт 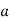 .
.
-
Розв’яжіть систему рівнянь
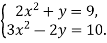
- Катет прямокутного трикутника відноситься до гіпотенузи як 5:13. Знайдіть периметр трикутника, якщо його другий катет дорівнює 24 см.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Моторний човен пройшов 20 км за течією річки і 32 км озером, затративши на весь шлях 4 год. Швидкість течії річки дорівнює 3 км/год. Знайдіть швидкість човна за течією річки.
-
Побудуйте графік функції
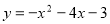 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- У прямокутній трапеції бічні сторони дорівнюють 24 см і 26 см, а менша діагональ є бісектрисою прямого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 17
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
- Запишіть 3 год 24 хв у хвилинах.
|
А |
Б |
В |
Г |
|
27 хв |
324 хв |
204 хв |
54 хв |
-
Чому дорівнює значення виразу
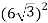 ?
?
|
А |
Б |
В |
Г |
|
18 |
36 |
54 |
108 |
- Укажіть хибне твердження:
|
А |
Б |
В |
Г |
|
–3 – ціле число |
–3 – недодатне число |
–3 – раціональне число |
–3 – невід’ємне число |
-
Знайдіть нулі функції
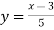 .
.
|
А |
Б |
В |
Г |
|
5 |
3 |
5 і 3 |
–3 |
-
Виконайте множення
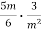 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Внесіть множник під знак кореня
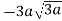 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
1.7. На рисунку зображено графік функції ![]() . Вкажіть проміжок спадання функції.
. Вкажіть проміжок спадання функції.

|
А |
Б |
В |
Г |
|
|
|
|
|
- Вкладник поклав до банку 1500 грн. Під який відсоток річних покладено гроші, якщо через рік на рахунку вкладника було 1725 грн.?
|
А |
Б |
В |
Г |
|
115% |
85% |
15% |
25% |
-
Який кут вертикальний з
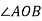 ?
?

|
А |
Б |
В |
Г |
|
|
|
|
|
- Знайдіть меншу основу рівнобічної трапеції, якщо висота, проведена з вершини тупого кута, ділить більшу основу на відрізки 4 дм і 16 дм.
|
А |
Б |
В |
Г |
|
10 дм |
12 дм |
16 дм |
8 дм |
1.11. На якому рисунку зображені рівнобедрені трикутники є подібними?

1.12. Відстань від точки А (1;2) до точки ![]() дорівнює 5. Знайдіть значення
дорівнює 5. Знайдіть значення ![]() .
.
|
А |
Б |
В |
Г |
|
–6; 2 |
–2 |
6 |
–2; 6 |
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
- Підприємець поклав у банк 50 000 грн. під 10% річних. Яка сума буде у нього на рахунку через 2 роки?
-
Знайдіть координати точок перетину прямої
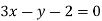 і параболи
і параболи 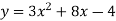 .
.
-
Знайдіть знаменник геометричної прогресії
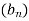 , у якої
, у якої 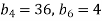 .
.
- Один із катетів прямокутного трикутника дорівнює 12 см, а інший – на 8 см менший за гіпотенузу. Знайдіть периметр трикутника.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Моторний човен пройшов 40 км проти течії річки і 28 км озером, затративши на шлях по озеру на 2 год менше, ніж на шлях по річці. Швидкість течії річки дорівнює 4 км/год. Знайдіть швидкість човна проти течії річки.
-
Побудуйте графік функції
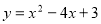 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- У прямокутній трапеції бічні сторони дорівнюють 36 см і 39 см, а більша діагональ є бісектрисою прямого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 18
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.
- Яка числова нерівність є правильною?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Виконайте ділення
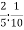 .
.
|
А |
Б |
В |
Г |
|
|
25 |
4 |
|
-
Скільки коренів має рівняння
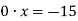 ?
?
|
А |
Б |
В |
Г |
|
безліч |
один |
жодного |
два |
-
Спростіть вираз
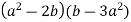 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Розв’язком якого рівняння є пара чисел
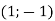 ?
?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Виконайте множення
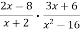 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
 На рисунку зображено графік функції
На рисунку зображено графік функції 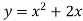 . Знайдіть множину розв’язків нерівності
. Знайдіть множину розв’язків нерівності 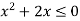 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
- Протягом восьмигодинного робочого дня робітник щогодини виготовляє 12; 10; 8; 11; 9; 12; 10; 8 деталей. Знайдіть середнє значення даної вибірки.
|
А |
Б |
В |
Г |
|
11 |
9 |
10 |
12 |
-
На рисунку зображено паралельні прямі
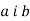 , які перетинає січна
, які перетинає січна 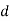 . Користуючись рисунком, знайдіть
. Користуючись рисунком, знайдіть 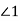 , якщо
, якщо 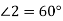 .
.

|
А |
Б |
В |
Г |
|
|
|
|
|
-
Один з кутів паралелограма дорівнює
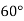 . Знайдіть решту його кутів.
. Знайдіть решту його кутів.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
У трикутнику
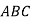
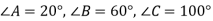 . Яка сторона трикутника є найбільшою?
. Яка сторона трикутника є найбільшою?
|
А |
Б |
В |
Г |
|
АС |
ВС |
Неможливо визначити |
АВ |
-
При якому значенні
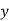 вектори
вектори 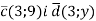 перпендикулярні?
перпендикулярні?
|
А |
Б |
В |
Г |
|
1 |
9 |
–1 |
3 |
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Розв’яжіть рівняння
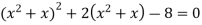 .
.
-
Розв’яжіть нерівність
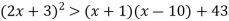 .
.
- Із натуральних чисел від 1 до 24 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 24?
-
У паралелограмі
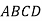 бісектриса кута А ділить сторону ВС на відрізки
бісектриса кута А ділить сторону ВС на відрізки 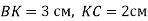 . Знайдіть периметр паралелограма.
. Знайдіть периметр паралелограма.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Катер проплив 24 км за течією річки і 48 км проти течії, витративши на весь шлях 4 год. Знайдіть швидкість катера за течією, якщо власна швидкість катера дорівнює 20 км ̸ год.
-
Побудуйте графік функції
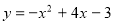 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- Діагональ рівнобічної трапеції з основами 25 см і 39 см є бісектрисою гострого кута. Знайдіть периметр і площу трапеції.
ЗАТВЕРДЖЕНО
Наказ директора школи
_________ №________
ВАРІАНТ 19
Частина 1
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на Вашу думку, відповідь і позначите її у бланку відповідей.

- Яку частину круга на рисунку заштриховано?
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Подайте у вигляді степеня вираз
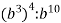 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайдіть значення аргументу, при якому функція
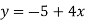 має значення 3.
має значення 3.
|
А |
Б |
В |
Г |
|
|
2 |
7 |
|
-
Спростіть вираз
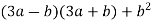 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Між якими двома послідовними натуральними числами міститься на координатній прямій число
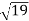 ?
?
|
А |
Б |
В |
Г |
|
3 і 4 |
4 і 5 |
5 і 6 |
6 і 7 |
1.6. На рисунку зображено графік функції ![]() . Вкажіть проміжок спадання функції.
. Вкажіть проміжок спадання функції.

|
А |
Б |
В |
Г |
|
|
|
|
|
1.7. Яку суму отримає вкладник через рік, якщо він поклав до банку 5000 грн. під 15% річних?
|
А |
Б |
В |
Г |
|
5750 грн. |
5015 грн. |
5075 грн. |
750 грн. |
-
Розв’яжіть нерівність
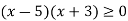 .
.
|
А |
Б |
В |
Г |
|
|
|
|
|
1.9. Визначте вид трикутника ![]() , якщо
, якщо ![]() .
.
|
А |
Б |
В |
Г |
|
гострокутний |
прямокутний |
Визначити неможливо |
тупокутний |
- Сторони трикутника відносяться як 7: 6: 4. Знайдіть більшу сторону подібного йому трикутника, менша сторона якого дорівнює 12 см.
|
А |
Б |
В |
Г |
|
84 см |
56 см |
14 см |
21 см |
- Точка М – середина відрізка АВ. Знайдіть координати точки М, якщо А(2; –3), В(–6; 7).
|
А |
Б |
В |
Г |
|
(4; –5) |
(–2; 2) |
(2; –2) |
(–4; 4) |
-
Обчисліть модуль вектора
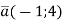 .
.
|
А |
Б |
В |
Г |
|
3 |
5 |
|
|
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
-
Знайдіть значення виразу
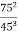 .
.
-
Знайдіть суму десяти перших членів арифметичної прогресії
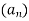 , якщо
, якщо  ,
, 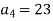 .
.
-
Скільки цілих чисел містить множина розв’язків нерівності
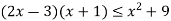 ?
?
-
У прямокутній трапеції гострий кут дорівнює
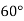 . Більша бічна сторона і більша основа дорівнюють по 12 см. Знайдіть середню лінію трапеції.
. Більша бічна сторона і більша основа дорівнюють по 12 см. Знайдіть середню лінію трапеції.
Частина третя
Розв’язання завдань 3.1 – 3.3 повинні мати обґрунтування. У них потрібно записати послідовно логічні дії та пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. При необхідності слід ілюструвати розв’язання схемами, графіками, таблицями.
- Моторний човен пройшов 28 км за течією річки і 40 км проти течії, затративши на шлях за течією на 2 год менше, ніж на шлях проти течії . Власна швидкість човна дорівнює 12 км/год. Знайдіть швидкість човна проти течії річки.
-
Побудуйте графік функції
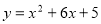 . Користуючись графіком, знайдіть:
. Користуючись графіком, знайдіть:
1) область визначення та область значень функції;
2) проміжки знакосталості функції;
3) проміжки зростання і спадання функції.
- Діагональ рівнобічної трапеції ділить середню лінію на відрізки 13 см і 23 см. Знайдіть периметр і площу трапеції.


про публікацію авторської розробки
Додати розробку
