Урок алгебри 9 клас."Числові послідовності. Способи задання послідовностей"
Ознайомити учнів з поняттям послідовності та способами її задання; формувати вміння і навички записувати послідовності, підбирати формулу n-го члена, перелічувати її властивості.
Урок № 45
Алгебра 9 клас
Дата:
Тема уроку. Числові послідовності. Способи задання послідовності
Мета уроку:
Навчальна: ознайомити учнів з поняттям послідовності та способами її задання; формувати вміння і навички записувати послідовності, підбирати формулу n-го члена, перелічувати її властивості.
Розвивальна: розвивати увагу, пам'ять, логічне мислення.
Виховна: виховувати культуру математичної мови, інтерес до вивчення нової теми, толерантність, повагу до думки іншого
Тип уроку: формування нових знань та вмінь
Обладнання: підручник А.Г. Мерзляк, 2017 рік, презентація учителя, проектор, екран, комп ’ютер
Девіз: „ Алгебра щедра. Частіше всього вона дає більше, чим у неї запитують”.
Хід уроку
- Організаційний етап
Перевірити готовність учнів до уроку, налаштувати на роботу.
- Мотивація навчальної та пізнавальної діяльності
В повсякденному житті ми часто зустрічаємося такими об’єктами, які для зручності пронумеровані, наприклад, місяці року, дні тижня, під’їзди та квартири будинку, вагони поїздів і т.д.. якщо говоримо про конкретний клас, то учень цього класу має свій порядковий номер у журналі. Що це за об’єкти ми сьогодні з вами і дізнаємося. Оголошення теми та мети уроку.
- Актуалізація опорних знань
Усні вправи
- Знайдіть значення виразу:
1) -2,6 + 0,5; 2) -2,1 : (-0,01); 3) (0,45)4 : 0,418;
4) ![]() ; 5)
; 5) 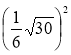 ; 6)
; 6) ![]() ;
;
7) (3 – ![]() )(3 +
)(3 + ![]() ).
).
-
Спростіть вираз:
1) (4b + 1) – (3 – b); 2)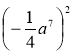 ; 3) (2x – 1)(х – 2);
; 3) (2x – 1)(х – 2);
4) а5 ∙ а12 : а16; 5) ![]() ; 6) 3x2y5 ∙ (-x3y2).
; 6) 3x2y5 ∙ (-x3y2).
- Знайдіть значення виразу:
1) х + 10у при х = 1,5, у = -![]() ; 2) 2x2 + 1 при х = -4;
; 2) 2x2 + 1 при х = -4;
3) х2 + 6х – 2 при х = 3.
Фронтальне опитування
- Які числові множини ви знаєте?
- Назвіть числовий ряд одноцифрових чисел.
- Цей ряд чисел скінченний чи нескінченний?
- А хто може назвати нескінченний ряд чисел?
- Формування нових знань
Об’єкти, які пронумеровані поспіль натуральними числами 1, 2. 3, …n, …, утворюють послідовності. Об’єкти, які утворюють послідовність, називають членами послідовності. Кожний член має свій номер. Наприклад,січень – це перший член послідовності місяців року, лютий – другий. Якщо член послідовності має номер n, то його називають n – им членом цієї послідовності. Ми з вами будемо мати справу з числовими послідовностями, тобто їх членами будуть числа і таку послідовність називають числовою.
|
Числова послідовність позначається так: (ап): а1; а2; а3; ...; ап. Кожне число ап — п-й член послідовності; п — номер члена. |
|||||||
|
Види числових послідовностей |
|||||||
|
1. Якщо кількість членів п послідовності (ап) скінченна, то (ап) — скінченна послідовність. Якщо кількість членів п послідовності (ап) нескінченна, то (ап) — нескінченна послідовність. Приклади: а) послідовність (ап) натуральних чисел нескінченна; б) послідовність (ап) коренів рівняння (х – 1)(х – 2)(х + 3) = 0 скінченна. |
|||||||
|
2. Якщо кожний наступний член послідовності, починаючи з другого, більший за попередній, то послідовність є зростаючою. Якщо кожний член послідовності, починаючи з другого, менший від попереднього, то послідовність є спадною. |
|||||||
|
Приклади: а) (ап): 1; 2; 3; ... — послідовність натуральних чисел є зростаючою; б) (bп): -1; -2; -3; ... — послідовність цілих від'ємних чисел є спадною. |
|||||||
|
Способи задання числових послідовностей: 1) описом знаходження її членів. Приклад. Числова послідовність дільників числа 15, записаних у порядку зростання: (ап): а1= 1; а2 = 3; а3 = 5; ...; а4 = 15; |
|||||||
|
2) переліком її членів. Приклад. (bn): 54; 1; 33; 27, тоді а1 = 54; а2 = 1; а3 = 33; а4 = 27; |
|||||||
|
3) таблицею. Приклад. |
|||||||
|
|
п |
1 |
2 |
3 |
4 |
5 |
|
|
|
ап |
-2 |
1 |
-4 |
1 |
-6 |
|
|
|
|||||||
|
Тоді а1 = -2; а2 = 1; а3 = - 4; а4 = 1; а5 = 6; |
|||||||
|
4) формулою п-го члена. Приклад. ап = п2 – 1, тоді а1 = 12 – 1 = 0; а2 = 22 – 1 = 3; а3 = 32 – 1 = 8 і т.д.; |
|||||||
|
5) рекурентною формулою. Приклад. ап = ап-1 ∙ ап-2, якщо а1 = 1; а2 = 2, тоді а1 = 1; а2 = 2; а3 = а1 ∙ а2 = 2; а4 = а2 ∙ а3 = 2 ∙ 2 = 4; а5 = а3 ∙ а4 = 4 ∙ 2 = 8. |
|||||||
Це спосіб задання послідовності за допомогою початкових умов і рекурентної формули.
IV. Формування вмінь
Усні вправи
1. Дано послідовність: 0,1; 7; 0,2; 8; 0,3; 9. Укажіть:
1) скільки членів має ця послідовність;
2) третій член послідовності;
3) який номер має член послідовності, що дорівнює 0,3;
4) який член послідовності є наступним за числом 8; попереднім до числа 7.
2. Послідовність (хп) задано формулою хп = п + 5. Укажіть перші три члени цієї послідовності. Чи є ця послідовність зростаючою? нескінченною?
Робота за підручником А.Г. Мерзляк, 2017 рік.

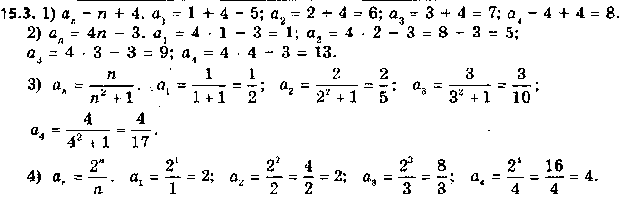
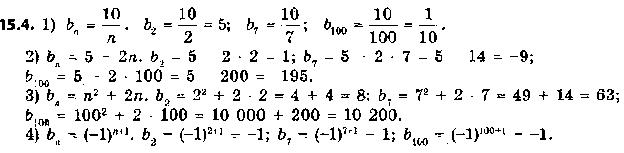
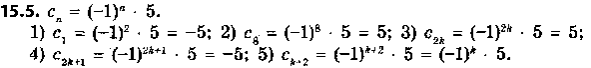
Робота в парі:
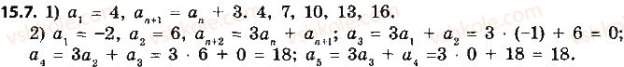
V. Підсумки уроку
Контрольні запитання
1. Наведіть приклади числових послідовностей.
2. Наведіть приклад числової послідовності: 1) скінченної; 2) нескінченної.
3. Наведіть приклад послідовності, заданої формулою п-го члена. Назвіть який-небудь член цієї послідовності.
4. Наведіть приклад послідовності, заданої рекурентною формулою.
- Рефлексія
- Я сьогодні взнав…
- Я навчився…
- Я не зрозумів…
- Я намагався…
- Домашнє завдання
§ 3, п.15 – опрацювати; №№ 15.2; 15.6; 15.10.


про публікацію авторської розробки
Додати розробку
