Розгорнутий конспект уроку: "Арифметична прогресія, її властивості"
Урок алгебри, 9 клас
Тема. Арифметична прогресія, її властивості.
Мета.
Ø Навчальна:
- Повторення та закріплення основних понять, властивостей з даної теми.
- Формування вмінь застосовувати властивості арифметичної прогресії до розв'язування вправ, знаходити n – ий член та суму n перших членів арифметичної прогресії,
Ø Виховна:
- Виховувати пізнавальний інтерес до математики
- Сприяти вихованню поваги одне одного в колективі
Ø Розвиваюча:
- Пізнавальний та інтелектуальний розвиток учнів
- Розвиток навичок логічного мислення
- Вміння аналізувати, узагальнювати, порівнювати, робити висновки
Тривалість уроку : 45 хвилин
Тип уроку. Урок застосування знань, навичок і умінь.
Етапи уроку
I.Організаційний момент (3 хвилини)
II.Мотивація навчальної діяльності (7 хвилин)
III.Актуалізація опорних знань (10 хвилин)
IV.Виконання практичних завдань (17 хвилин)
V.Підсумок уроку (6 хвилини)
VI.Постановка домашнього завдання (2 хвилини)
Хід уроку
I.Організаційний момент
(Зайшовши до класу, спостерігаю за реакцією дітей.)
Добрий день, діти! (Вітаюсь, після заспокоєння учнів). Ну що, на перерві відпочили? А тепер давайте будемо налаштовуватись на урок. Перш за все відмітимо відсутніх.
II.Мотивація навчальної діяльності
Діти, скажіть мені, будь ласка, чого ви очікуєте від сьогоднішнього уроку? (Заслуховую відповіді учнів). Я все зрозуміла, думаю сказане вами здійсниться. А епіграфом (на дошці записано епіграф уроку) нашого уроку є такі слова:
«Прогресія – це рух вперед».
Перша умова, якої треба дотримуватися в математиці, – це бути точним.
Друга – бути чітким,
І наскільки можливо, простим.
Отже, ми сьогодні з вами на уроці просто, чітко і з легкістю узагальнимо знання з теми: « Арифметична прогресія», закріпимо навички обчислення елементів прогресії, покажемо практичне застосування теми на прикладах історичних задач, та використання теми навколишньому житті. Тому я очікую злагодженої роботи, взаємодопомоги, взаємоповаги, гарних результатів.
III.Актуалізація опорних знань
Перш за все ми повинні згадати раніше вивчений матеріал. Дайте відповіді на поставлені мною запитання (фронтальне опитування):
1.Сформулюйте означення числової послідовності. (Це функція, задана на множині усіх натуральних чисел або на множині перших n натуральних чисел).
2.Що називається арифметичною прогресією? (Послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число).
3.Що таке різниця арифметичної прогресії? (Стале для певної послідовності число, на яке змінюється кожен наступний член, починаючи з другого).
4.Яку арифметичну прогресію називають зростаючою, а яку спадною? (Зростаюча, якщо її різниця додатна, а спадна – якщо її різниця від'ємна).
5. Назвіть основну властивість арифметичної прогресії (Будь-який член арифметичної прогресії, крім першого, дорівнює півсумі двох сусідніх з них членів)
6.Як виражається n-й член арифметичної прогресії через її перший член і різницю?
7.Чому дорівнює сума двох членів скінченної арифметичної прогресії , рівновіддалених від її кінців?(
8.Чому дорівнює сума n перших членів арифметичної прогресії?
Добре, все пригадали, молодці! А тепер спробуємо пограти в гру, яка вам повинна бути знайома. Називається вона «Вірю – не вірю». Я задаватиму запитання, а ви повинні погодитися з цим твердженням чи ні, говорячи мені «Вірю» чи «Не вірю». Спробуємо?
Чи вірите ви, що:
1)Послідовність простих чисел є скінченною?
2)Послідовність неправильних дробів зі знаменником 10 є нескінченною?
3)Послідовність 5, 8, 11, 14… арифметична прогресія?
4)Послідовність 1, 1, 1, 1… арифметична прогресія?
5)Послідовність 0, 0, 0, 0.. арифметична прогресія?
6)Послідовність 1, -1, 1, -1… арифметична прогресія?
7)Арифметична прогресія -12, -10, -8… спадна?
8)Арифметична прогресія 14, 4, -6… зростаюча?
9)У арифметичній прогресії 4, 9, 14, різниця дорівнює 5, а четвертий член 18?
10) У арифметичні прогресії -18, -15, -12 різниця дорівнює -3?
11) У арифметичній прогресії -5, -1, 3… сьомий член дорівнює 19?
12) В арифметичній прогресії а20 = 61 при умові, що а1=4, а d=3?
13) Сума перших двадцяти членів арифметичної прогресії 5, 7, 9 дорівнює 480?
14) Арифметична прогресія – це лінійна функція, задана на множині натуральних чисел?
Ну що, сподобалось?
IV.Виконання практичних завдань
А зараз ви побачите, як арифметична прогресія використовується в житті та розглянемо старовинні задачі видатних людей. Подивіться на цей плакат з незрозумілими числами. Це послання до нас потрапило від американського вченого, математика і філософа Норберта Вінера. Щоб зрозуміти його, нам потрібно розв'язати низку задач. (На картках надруковані задачі, а з іншого боку – фрагмент висловлення). Вам потрібно взяти картку, розв'язати задачу біля дошки, знайти відповідь на плакаті і приклеїти цю картку. (Задачі обговорюються разом)
(Кожна задача розміщена на окремій картці)
Задача 1. Стародавня арабська задача. Знайдіть 20-й член і суму двадцяти членів арифметичної прогресії 3, 7, 11, 15, …(79)
Задача 2. Учитель запропонував знайти суму всіх натуральних чисел від 1 до 40; вважав, що школярі довго додаватимуть сорок чисел. А малий Карл Гаусс завдання виконав за хвилину. Як він це зробив? Яка буде сума? (800)
Задача 3. Ресора складається з десяти сталевих смуг. Довжина верхньої смуги 105 см, а кожна інша на 9 см коротша від попередньої. Знайдіть суму довжин усіх смуг ресори. (645)
Задача 4. Стародавня задача. Людям, які копають криницю, обіцяно за перший метр заплатити 30 крб., а за кожний наступний – на 20 крб. більше, ніж за попередній метр. Скільки вони одержать за копання 12-метрової криниці? (1680)
Задача 5. Задача Феофана Прокоповича. Якась людина має багато коней, і всім їм різна ціна. Найгірший кінь коштує 4 золотих, а найкращий – 55 золотих, і ціна від одного коня до другого весь час зростає на 3 золотих. Питаємо: скільки ж усього було коней? (18)
Задача 6. Задача Франкера. Скільки разів проб'є годинник упродовж 12 годин, якщо від відбиває щопівгодини? (90)
Задача 7. Першого дня магазин продав 18кг цукру, а кожного наступного дня продавав на 2кг більше, ніж попереднього. Скільки цукру було продано за 10 днів? (180)
Задача 8. При вільному падінні фізичне тіло проходить за першу секунду 4, 9 м, а кожну наступну – на 9, 8 м більше. Знайдіть глибину шахти, якщо камінець досяг її дна через 8 с після початку падіння. (314)
Задача 9. Курс водяних процедур починають проводити 15хв в перший день і збільшують кожного наступного дня на 10хвилин. Скільки днів потрібно приймати процедури, щоб вони тривали 1годину 45хвилин? (10)
Задача 9. Працівники повинні викласти плиткою 288м2. Набуваючи досвіду, кожний наступний день, починаючи з другого, вони викладали на 2м2 більше, ніж у попередній. І запасів плитки їм вистачить рівно на 11 днів. Плануючи, що продуктивність праці буде збільшуватися таким же чином, бригадир визначив, що для завершення роботи знадобиться ще 5 днів. Скільки м2 плитки поклали в перший день? (3)
V.Підсумок уроку
Як бачимо ми всі разом відкрили послання. Воно звучить так: «Математика – наука молодих. Інакше й не може бути. Заняття математикою – це така гімнастика розуму, для якої потрібна вся гнучкість і вся витривалість молодості».
Я приєднуюсь до слів Норберта Вінера і наголошую, що математика – це не тільки шкільний предмет, а й знання, які потрібні у будь – яких сферах нашого життя. Тому, шановні діти, учіть математику поки молоді, і поки вона вам під силу.
VI.Постановка домашнього завдання
Я дякую вам за увагу, активність і роботу на уроці. Запишіть будь ласка завдання додому. §21 повторити, №918 - №923 (Бевз Г.П., Бевз В.Г. Алгебра: Підруч. Для 9кл., 2009р.).
Урок алгебри, 9 клас
Тема. Арифметична прогресія, її властивості.
Мета.
- Навчальна:
- Повторення та закріплення основних понять, властивостей з даної теми.
- Формування вмінь застосовувати властивості арифметичної прогресії до розв’язування вправ, знаходити n – ий член та суму n перших членів арифметичної прогресії,
- Виховна:
- Виховувати пізнавальний інтерес до математики
- Сприяти вихованню поваги одне одного в колективі
- Розвиваюча:
- Пізнавальний та інтелектуальний розвиток учнів
- Розвиток навичок логічного мислення
- Вміння аналізувати, узагальнювати, порівнювати, робити висновки
Тривалість уроку : 45 хвилин
Тип уроку. Урок застосування знань, навичок і умінь.
Етапи уроку
- Організаційний момент (3 хвилини)
- Мотивація навчальної діяльності (7 хвилин)
- Актуалізація опорних знань (10 хвилин)
- Виконання практичних завдань (17 хвилин)
- Підсумок уроку (6 хвилини)
- Постановка домашнього завдання (2 хвилини)
Хід уроку
- Організаційний момент
(Зайшовши до класу, спостерігаю за реакцією дітей.)
Добрий день, діти! (Вітаюсь, після заспокоєння учнів). Ну що, на перерві відпочили? А тепер давайте будемо налаштовуватись на урок. Перш за все відмітимо відсутніх.
- Мотивація навчальної діяльності
Діти, скажіть мені, будь ласка, чого ви очікуєте від сьогоднішнього уроку? (Заслуховую відповіді учнів). Я все зрозуміла, думаю сказане вами здійсниться. А епіграфом (на дошці записано епіграф уроку) нашого уроку є такі слова:
«Прогресія – це рух вперед».
Перша умова, якої треба дотримуватися в математиці, – це бути точним.
Друга – бути чітким,
І наскільки можливо, простим.
Отже, ми сьогодні з вами на уроці просто, чітко і з легкістю узагальнимо знання з теми: « Арифметична прогресія», закріпимо навички обчислення елементів прогресії, покажемо практичне застосування теми на прикладах історичних задач, та використання теми навколишньому житті. Тому я очікую злагодженої роботи, взаємодопомоги, взаємоповаги, гарних результатів.
- Актуалізація опорних знань
Перш за все ми повинні згадати раніше вивчений матеріал. Дайте відповіді на поставлені мною запитання (фронтальне опитування):
- Сформулюйте означення числової послідовності. (Це функція, задана на множині усіх натуральних чисел або на множині перших n натуральних чисел).
- Що називається арифметичною прогресією? (Послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число).
- Що таке різниця арифметичної прогресії? (Стале для певної послідовності число, на яке змінюється кожен наступний член, починаючи з другого).
- Яку арифметичну прогресію називають зростаючою, а яку спадною? (Зростаюча, якщо її різниця додатна, а спадна – якщо її різниця від’ємна).
-
Назвіть основну властивість арифметичної прогресії (Будь-який член арифметичної прогресії, крім першого, дорівнює півсумі двох сусідніх з них членів:
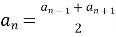 )
)
-
Як виражається n-й член арифметичної прогресії через її перший член і різницю?(
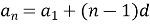 ).
).
-
Чому дорівнює сума двох членів скінченної арифметичної прогресії , рівновіддалених від її кінців?(
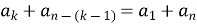 )
)
- Чому дорівнює сума n перших членів арифметичної прогресії?
(![]() ).
).
Добре, все пригадали, молодці! А тепер спробуємо пограти в гру, яка вам повинна бути знайома. Називається вона «Вірю – не вірю». Я задаватиму запитання, а ви повинні погодитися з цим твердженням чи ні, говорячи мені «Вірю» чи «Не вірю». Спробуємо?
Чи вірите ви, що:
- Послідовність простих чисел є скінченною?
- Послідовність неправильних дробів зі знаменником 10 є нескінченною?
- Послідовність 5, 8, 11, 14… арифметична прогресія?
- Послідовність 1, 1, 1, 1… арифметична прогресія?
- Послідовність 0, 0, 0, 0.. арифметична прогресія?
- Послідовність 1, -1, 1, -1… арифметична прогресія?
- Арифметична прогресія -12, -10, -8… спадна?
- Арифметична прогресія 14, 4, -6… зростаюча?
- У арифметичній прогресії 4, 9, 14, різниця дорівнює 5, а четвертий член 18?
- У арифметичні прогресії -18, -15, -12 різниця дорівнює -3?
- У арифметичній прогресії -5, -1, 3… сьомий член дорівнює 19?
- В арифметичній прогресії а20 = 61 при умові, що а1=4, а d=3?
- Сума перших двадцяти членів арифметичної прогресії 5, 7, 9 дорівнює 480?
- Арифметична прогресія – це лінійна функція, задана на множині натуральних чисел?
Ну що, сподобалось?
- Виконання практичних завдань
А зараз ви побачите, як арифметична прогресія використовується в житті та розглянемо старовинні задачі видатних людей. Подивіться на цей плакат з незрозумілими числами. Це послання до нас потрапило від американського вченого, математика і філософа Норберта Вінера. Щоб зрозуміти його, нам потрібно розв’язати низку задач. (На картках надруковані задачі, а з іншого боку – фрагмент висловлення). Вам потрібно взяти картку, розв’язати задачу біля дошки, знайти відповідь на плакаті і приклеїти цю картку. (Задачі обговорюються разом)
(Кожна задача розміщена на окремій картці)
Задача 1. Стародавня арабська задача. Знайдіть 20-й член і суму двадцяти членів арифметичної прогресії 3, 7, 11, 15, …(79)
Задача 2. Учитель запропонував знайти суму всіх натуральних чисел від 1 до 40; вважав, що школярі довго додаватимуть сорок чисел. А малий Карл Гаусс завдання виконав за хвилину. Як він це зробив? Яка буде сума? (800)
Задача 3. Ресора складається з десяти сталевих смуг. Довжина верхньої смуги 105 см, а кожна інша на 9 см коротша від попередньої. Знайдіть суму довжин усіх смуг ресори. (645)
Задача 4. Стародавня задача. Людям, які копають криницю, обіцяно за перший метр заплатити 30 крб., а за кожний наступний – на 20 крб. більше, ніж за попередній метр. Скільки вони одержать за копання 12-метрової криниці? (1680)
Задача 5. Задача Феофана Прокоповича. Якась людина має багато коней, і всім їм різна ціна. Найгірший кінь коштує 4 золотих, а найкращий – 55 золотих, і ціна від одного коня до другого весь час зростає на 3 золотих. Питаємо: скільки ж усього було коней? (18)
Задача 6. Задача Франкера. Скільки разів проб’є годинник упродовж 12 годин, якщо від відбиває щопівгодини? (90)
Задача 7. Першого дня магазин продав 18кг цукру, а кожного наступного дня продавав на 2кг більше, ніж попереднього. Скільки цукру було продано за 10 днів? (180)
Задача 8. При вільному падінні фізичне тіло проходить за першу секунду 4, 9 м, а кожну наступну – на 9, 8 м більше. Знайдіть глибину шахти, якщо камінець досяг її дна через 8 с після початку падіння. (314)
Задача 9. Курс водяних процедур починають проводити 15хв в перший день і збільшують кожного наступного дня на 10хвилин. Скільки днів потрібно приймати процедури, щоб вони тривали 1годину 45хвилин? (10)
Задача 9. Працівники повинні викласти плиткою 288м2. Набуваючи досвіду, кожний наступний день, починаючи з другого, вони викладали на 2м2 більше, ніж у попередній. І запасів плитки їм вистачить рівно на 11 днів. Плануючи, що продуктивність праці буде збільшуватися таким же чином, бригадир визначив, що для завершення роботи знадобиться ще 5 днів. Скільки м2 плитки поклали в перший день? (3)
- Підсумок уроку
Як бачимо ми всі разом відкрили послання. Воно звучить так: «Математика – наука молодих. Інакше й не може бути. Заняття математикою – це така гімнастика розуму, для якої потрібна вся гнучкість і вся витривалість молодості».
Я приєднуюсь до слів Норберта Вінера і наголошую, що математика – це не тільки шкільний предмет, а й знання, які потрібні у будь – яких сферах нашого життя. Тому, шановні діти, учіть математику поки молоді, і поки вона вам під силу.
- Постановка домашнього завдання
Я дякую вам за увагу, активність і роботу на уроці. Запишіть будь ласка завдання додому. §21 повторити, №918 - №923 (Бевз Г.П., Бевз В.Г. Алгебра: Підруч. Для 9кл., 2009р.).
1


про публікацію авторської розробки
Додати розробку
