Брошура "Геометрія трикутника"
СЕЛЕЩИНСЬКА ЗАГАЛЬНООСВІТНЯ ШКОЛА І –ІІІ СТУПЕНІВ

Іванякова Н. І.


ВСТУП
У пропонованій брошурі розглянуто найважливіші властивості трикутників. Її мета – заповнити прогалину в знаннях учнів щодо геометрії трикутника. Різні властивості трикутника досліджували не тільки любителі елементарної геометрії, а й найвідоміші вчені всіх епох: Евклід, Архімед, Піфагор, Гаусс та інші. Виявлені та доведені ними властивості трикутників- справжні перлини людського мислення. Багато з них доступні для розуміння учнями загальноосвітніх шкіл і було б несправедливо і нерозумно приховувати їх від школярів. Геометрія трикутника дає чудовий матеріал для досліджень математиків – початківців, у ній кожен може знайти цікаві і доступні теми для самостійних пошуків. Особливо це стосується учнів, які поглиблено вивчають математику.
Більшість пропонованих теорем і задач спеціалістам відомі давно, їх запозичено з праць відомих математиків, математичних журналів, збірників завдань різних олімпіад. А деякі властивості виявлені і обгрунтовані самостійно.
Матеріал можна розглядати як додаток до шкільного підручника геометрії. Трикутники вивчають і використовують і в основній школі, і в старших класах. Правда, через обмаль часу в школі доводиться обмежуватися тільки найважливішими властивостями трикутників. Все ж учителям математики бажано знати більше, ніж є у підручниках для школярів.
Пропонована добірка задач пов’язана з конструкцією, в якій відома різна група елементів трикутника. При цьому виникають різні цікаві закономірності та корисні співвідношення між елементами трикутника. Запропонована серія задач буде доречною як на уроці, так і під час роботи математичного гуртка або факультативу.
Матеріал розрахований на вчителів математиків та учнів, які поглиблено вивчають математику.
РОЗДІЛ І
Прямокутні трикутники
ЗАДАЧА 1. Відома висота hc опущена з вершини прямого кута і гострий
кут А.
Роз’вязати трикутник.
Розв’язання

-
У ∆ АDC b =
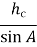 = AC
= AC
-
У ∆ ВDC a =
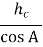 = BC
= BC
-
 У ∆ AВC с =
У ∆ AВC с = 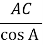 =
=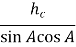 =
=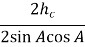 =
=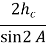
- <B= 900 - <A
ЗАДАЧА 2. Відома медіана проведена з вершини прямого кута до
гіпотенузи і гострий кут А. Розв’язати трикутник
Розв’язання
-
 Гіпотенуза АВ =2mc=c.
Гіпотенуза АВ =2mc=c.
-
AC =b =c

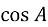 = 2mc
= 2mc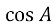 .
.
-
BC = a =c

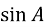 = 2mc
= 2mc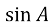 .
.
-
 <B= 900 - <A
<B= 900 - <A
ЗАДАЧА 3. Довести, що кут між висотою, опущеною на гіпотенузу, і
катетом, дорівнює куту між медіаною, проведеною до
гіпотенузи, і іншим катетом.
Доведення
- ∆ АCD ~ ∆ АBC, бо у них є по прямому куту
(<АСB= 900 і <АDС= 900 ), кут САВ – спільний.
![]()
![]() Тому <АСD = <АBС.
Тому <АСD = <АBС.
 2.Медіана mc= CM =
2.Медіана mc= CM = ![]() AB = MB → ∆ CMB -
AB = MB → ∆ CMB -
рівнобедрений з основою ВС ; <B = <С.
3. За законом транзитивності :
<АСD = <АВС, <АВС = <BСМ →<АСD =<ВСМ
ЗАДАЧА 4. Знайти відношення сторін прямокутного трикутника,
висоти і проекцій катетів на гіпотенузу.
Розв’язання
![]() 1.∆ АDC ~ ∆ CDB ~∆ АCB (доведення у задачі 3).
1.∆ АDC ~ ∆ CDB ~∆ АCB (доведення у задачі 3).
 2. Складаємо відношення більшого катета до гіпотенузи у кожному трикутнику, починаючи з більшого трикутника.
2. Складаємо відношення більшого катета до гіпотенузи у кожному трикутнику, починаючи з більшого трикутника.
![]() =
=![]() =
=![]() → h=
→ h=![]() ; b2 = c
; b2 = c ![]() bc , або b=
bc , або b= ![]()
( b – середнє – геометричне гіпотенузи і проекції катета на гіпотенузу).
3. Складаємо відношення малого катета до гіпотенузи, починаючи з більшого
трикутника:
![]() =
=![]() =
=![]() → h=
→ h=![]() ; a2 = c
; a2 = c ![]() ac , або a=
ac , або a= ![]() .
.
4. Складаємо відношення малого катета , починаючи з більшого трикутника.
![]() =
=![]() =
=![]() → h2 =ac
→ h2 =ac![]() bc або h=
bc або h= ![]() .
.
ЗАДАЧА 5. Дано сторони прямокутного трикутника. Знайти радіус
вписаного кола.
Розв’язання
-

 Центр вписаного кола у кут належить бісектрисі кута.
Центр вписаного кола у кут належить бісектрисі кута.
-
 Радіус завжди перпендикулярний до дотичної
Радіус завжди перпендикулярний до дотичної
![]()
![]()
![]()
![]() ON BC, OM AB, OK AC.
ON BC, OM AB, OK AC.
- Дотичні, що виходять з однієї точки, рівні , тому АК=АМ=m,
CK= CN= r, BM= BN= n. AB=c, BC=a, AC=b.
![]() Складаємо систему: с= m +n,
Складаємо систему: с= m +n,
a= n +r,
b = m +r.
![]() З другого і третього рівняння визначимо m і n та підставимо їх значення у перше рівняння с= m +n,
З другого і третього рівняння визначимо m і n та підставимо їх значення у перше рівняння с= m +n,
n = а - r,
m = b - r.
c = a – r +b – r = a + b – 2r. Визначимо r.
2r = a +b – c , r = ![]() (a +b – c ).
(a +b – c ).
ЗАДАЧА 6. У прямокутному трикутнику дано висоту h і бісектрису L
проведені до гіпотенузи. Розв’язати трикутник.
Розв’язання
![]()
![]() 1.Розглянемо прямокутний трикутник HCL
1.Розглянемо прямокутний трикутник HCL

![]() HCL =
HCL = ![]() =
=![]()
2. ![]() = 450,
= 450, ![]() =450 +
=450 + ![]() .
.
3. ![]() = 450 –
= 450 – ![]() .
.
4. Але![]() =
= ![]() = 450 +
= 450 + ![]() =
= ![]() .
.
5. Далі трикутник розв’язується за задачею 1 ( дано висота і кут ).
ЗАДАЧА 7. У прямокутному трикутнику дано гострий кут А і суму
катетів а + b. Розв’язати трикутник.
Розв’язання
 Нехай a + b = m.
Нехай a + b = m.
1.![]() +
+![]() = 900,
= 900, ![]() =900 -
=900 - ![]() .
.
2. Відомо, що ![]() =ctq
=ctq![]() , або a = b ctq
, або a = b ctq![]() .
.
Але (за умовою) a = m – b. Порівняємо праві
сторони:
m – b= b ctq![]() ,
,
m = b + b ctq![]() ,
,
m = b(1+ ctq![]() ),
),
b =![]()
-
a= b ctq
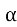 =
= 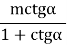 .
.
-
c =
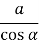 =
= 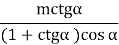 =
= 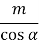
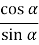
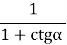 =
= 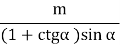
ЗАДАЧА 8. У прямокутному трикутнику дано різницю катетів і
гострий кут В. Розв’язати трикутник.
Розв’язання.
Малюнок до задачі 7.
Нехай b – a =n, ![]() =
=![]() .
.
-
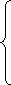
 = tq
= tq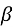 ,
,
→ b – n = b tq![]() , n = b -b tq
, n = b -b tq![]() , n = b(1 - tq
, n = b(1 - tq![]() ,
,
a =b – n.
b = ![]()
-
a = b tg
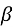 =
=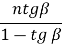 .
.
-
c =
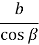 =
= 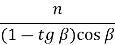 .
.
-
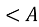 = 900 -
= 900 - 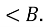
ЗАДАЧА 9. З точки кола радіуса R проведено дві хорди а і b. Знайти
центральні кути, які спираються на ці хорди ( хорди стягують
центральні кути ).
Розв’язання
І спосіб
-
 ОВС і
ОВС і  ОАС – рівнобедрені так, як утворені двома радіусами.
ОАС – рівнобедрені так, як утворені двома радіусами.
-




 Побудуємо перпендикуляр до ВС. ОК = R. Радіус перпендикулярний до хорди , ділить її пополам.
Побудуємо перпендикуляр до ВС. ОК = R. Радіус перпендикулярний до хорди , ділить її пополам.
![]()
 МС =
МС =![]() .
.
-
Тоді
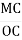 =
= 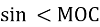 , або
, або 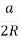 =
= 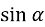 ,
,
![]() =arcsin
=arcsin ![]() ,
, ![]() ВОС = 2arcsin
ВОС = 2arcsin![]()
-
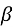 = arcsin
= arcsin 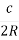 ,
, 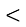 COA = 2arcsin
COA = 2arcsin 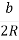 .
.
ІІ спосіб ( Цей спосіб застосовується для довільних трикутників)
За теоремою косинусів :
-
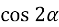 =
=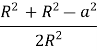 =
= 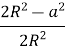 = 1 -
= 1 - 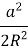 ,
,
2![]() = arccos (1 -
= arccos (1 - ![]() ).
).
-
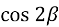 =
= 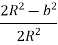 = 1 -
= 1 - 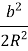 ,
,
2![]() = arccos (1 -
= arccos (1 - ![]() ).
).
РОЗДІЛ ІІ
Рівнобедрені трикутники
ЗАДАЧА 10. Знайти радіус описаного кола , якщо відома бічна сторона
трикутника і висота проведена до основи.
Розв’язання
Якщо коло описане навколо рівнобедреного трикутника, то центр кола належить висоті, опущеної до основи. Радіус перпендикулярний до хорди ділить її навпіл. Тому перетин серединного перпендикуляра до бічного ребра з висотою є центр описаного кола. Радіус знаходиться за формулою:
R = ![]() .
.
Доведемо це.
-

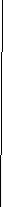
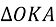
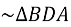 , так як
, так як 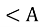 - спільний,
- спільний, 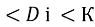 - прямі кути.
- прямі кути.
-
 =
= 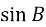 ,
,
-
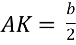 ,
,
-

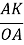 =
= 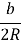 =
= 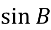 ,
, 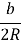 =
=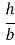
 R =
R = 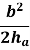 .
.
ЗАДАЧА 11. Дано бічну сторону b і кут В при основі. Знайти радіус
описаного кола.
Розв’язання
Малюнок і формули задачі 10.
-
h = b
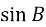
-
R =
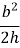 =
=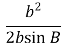 =
=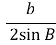 ( а це є наслідок теореми синусів)
( а це є наслідок теореми синусів)
ЗАДАЧА 12. Дано бічну сторону b і кут А при вершині . Знайти радіус
описаного кола.
Розв’язання
Малюнок задачі 1.
-
AD – бісектриса, висота і медіана трикутника, тому
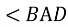 =
= 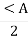 .
.
-
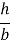 =
= 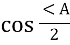 , h = b
, h = b 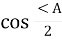 .
.
-
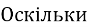
R = ![]() , то R =
, то R = 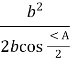 =
=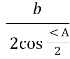 .
.
ЗАДАЧА 13. Дано основу а і кут при основі В. Знайти радіус описаного
кола.
Розв’язання.
- Сума кутів трикутника - 1800.
![]() + 2
+ 2![]() = 1800 ,
= 1800 , ![]() = 1800 - 2
= 1800 - 2![]() .
.
- За наслідком теореми синусів :
R = ![]() =
=![]() =
= ![]() .
.
ЗАДАЧА 14. У трикутнику дано бічну сторону b і медіану проведену до
цієї бічної сторони. Розв’язати трикутник.
Розв’язання
-


 З
З 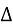 ВКС, КС =
ВКС, КС =  , за теоремою косинусів
, за теоремою косинусів
![]() =
= ![]() +
+ ![]() - ab
- ab![]() =
= ![]() +
+ ![]() - ab
- ab![]() ,
,
бо ![]() =
= ![]() ( 1800 -
( 1800 - ![]() ).
).
![]() =
= ![]() +
+ ![]() - ab
- ab![]() )=
)= ![]() +
+ ![]() -ab
-ab![]() .
.
-
У
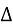 ADC : DC =
ADC : DC =  ,
, 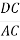 =
= 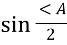 ,
,  =
= 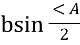 ,
,
тоді ![]() =
= ![]() +
+ ![]() - a
- a![]()
![]() =
= ![]() +
+ ![]() -
- ![]() ,
,
![]() =
= ![]() +
+ ![]() . Знайдемо a
. Знайдемо a
![]() =
= ![]() -
- ![]() , a=
, a= 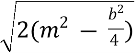 =
= 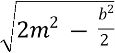 ,
,
3.![]() =
= 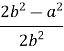 = =
= = 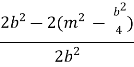 =
= 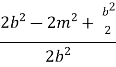 =
= 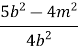 .
.
ЗАДАЧА . Знайти висоту проведену до бічної сторони b
рівнобедреного трикутника, якщо його основа а.
Розв’язання
І спосіб
-
 h2 = a2 –x2 (у меншому трикутнику );
h2 = a2 –x2 (у меншому трикутнику );
h2 = b2 –(b - x)2 (у більшому трикутнику);
- Порівняємо праві частини, розкриємо дужки, зведемо подібні доданки, знайдемо х.
a2 –x2= b2 –(b2 -2b![]() x2),
x2),
a2 –x2= b2 –b2 + 2b![]() x2),
x2),
![]() a2 = 2b
a2 = 2b![]() , x =
, x =![]()
-
h2 = a2 -
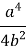 =
= 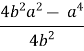 =
= 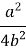 (4b2 – a2)
(4b2 – a2)
h= ![]()
ІІ спосіб
За формулою Герона S = ![]() ,де p =
,де p = ![]() .
.
За іншою формулою S= ![]() hb
hb![]() .
.
Прирівняємо праві частини ![]() h
h![]() =
= ![]()
h = 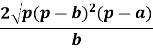
ІІІ спосіб
За теоремою косинусів ![]() =
= 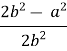
h= b![]() , але
, але ![]() =
= ![]() = =
= =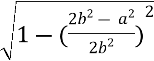 =
=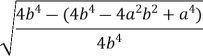 =
=
= 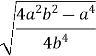 =
= 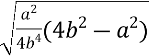 =
= 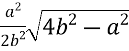 .
.
h= ![]()
ІІІ РОЗДІЛ
Застосування теореми синусів, косинусів і їх наслідків
при розв’язуванні трикутників
Лема:
![]() =
= ![]() =
= ![]() = R (задача 11);
= R (задача 11);
Нехай b= ![]() a , c=
a , c=![]() a
a
![]() =
=![]() ,
, ![]() =
=![]() , Тоді маємо:
, Тоді маємо:
![]() =
= ![]() =
= ![]() = R. Знайдемо суму лівої сторони:
= R. Знайдемо суму лівої сторони:
![]() = R,
= R, ![]() =
=![]() = R.
= R.
Але ![]() = p ( півпериметр), а
= p ( півпериметр), а ![]() .
.
Це означає:
- Якщо відомо периметр і два кути, то задача розв’язується.
-
R=
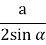 , тоді
, тоді 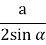 =
=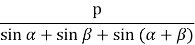 , звідси
, звідси
a = ![]() =
=![]() , аналогічно
, аналогічно
b =![]() ,
,
c= ![]() .
.
ЗАДАЧА 15. Відомі три сторони трикутника. Знайти радіус вписаного
кола.
Розв’язання
Впишемо коло у довільний трикутник. Центр кола належить перетину бісектрис , а радіус і дотична перпендикулярні.
Розглянемо площу трикутника АВС . Вона є сумою трьох менших трикутників.
![]() =
= ![]() +
+ ![]() +
+ ![]() ,
,
-

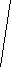
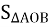 =
= c
c r ,
r ,

![]()
![]()
![]()
![]()

![]() =
= ![]() b
b![]() r ,
r ,
![]() =
= ![]() a
a![]() r ,
r ,
2 . S = ![]() r (a +b + c) = r
r (a +b + c) = r![]() , r =
, r = ![]() .
.
3 . S = ![]() , тоді
, тоді
R = 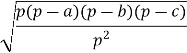 =
= ![]() .
.
ЗАДАЧА 15(a). Дано радіус вписаного кола і сторони трикутника.
Знайти кути трикутника.
Розв’язання
![]() AM = AK = m,
AM = AK = m,
CK = CN =n, як дотичні, що виходять з однієї точки.
BM = BN = q.
Тоді tg ![]() =
= ![]() ,
,
![]() a = q+ n ,
a = q+ n ,
![]() tg
tg ![]() =
= ![]() , b = m+ n ,
, b = m+ n ,
c = m + q.
tg ![]() =
= ![]() .
.
Додамо рівності:
a +b + c = 2 (m + n+ q ),
P=![]() = m + n+ q .
= m + n+ q .
m = p – (n+q) = p – a ,
n = p – (m+q) = p – c ,
q = p – (m+n) = p – b ,
tg ![]() =
= ![]() =
= 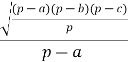 =
= ![]() ;
;
tg ![]() =
= ![]() ; tg
; tg ![]() =
= ![]() .
.
Наслідок.
Якщо дано периметр , сторони і протилежний кут, то радіус
вписаного кола можна обчислити за формулою
r = (p – a) tg ![]() = (p – b) tg
= (p – b) tg ![]() = (p – c) tg
= (p – c) tg ![]() , де р – півпериметр.
, де р – півпериметр.
ЗАДАЧА 16. Довести, що ![]() =
= ![]() .
.
Доведення
За наслідком теореми синусів ![]() =
= ![]() .
.
До кожної частини рівняння додамо по 1 і віднімемо по 1. Маємо:
![]() + 1=
+ 1= ![]() + 1 ,
+ 1 , ![]() =
= ![]() .
.
Аналогічно : ![]() - 1=
- 1= ![]() - 1 ,
- 1 , ![]() =
= ![]() .
.
Знайдемо відношення: ![]() =
= ![]() .
.
Перетворимо суму і різницю у добуток.
![]() =
= 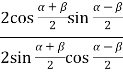 =
= 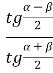 , аналогічно:
, аналогічно:
![]() =
= 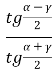 ,
, ![]() =
= ![]() .
.
ЗАДАЧА 17. (Геометрія 7 – 11, Погорєлов О. В. №)
Довести,що бісектриса кута ділить протилежну сторону
на пропорційні відрізки, пропорційність яких задають
прилеглі сторони ![]() =
= ![]() .
.
Доведення

![]()
-
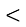 ACD =
ACD = 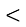 BCD=
BCD=  .Нехай
.Нехай 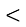 ADC=
ADC=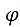 ,
,
![]()
![]() BDC=1800 – .
BDC=1800 – .
![]()
![]()
![]() =
= ![]() ,
, ![]() =
= 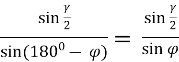
2 . Праві сторони рівні – порівняємо ліві сторони.
![]() =
= ![]()
![]() =
= ![]()
![]()
![]() =
= ![]() .
.
ЗАДАЧА 18. У довільному трикутнику відомі кути при основі і одна
бічна сторона. Знайти бісектрису, проекції сторін на основу.
Розв’язання
Нехай відомі AC = b, ![]() A і
A і ![]() B.
B.
-
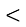 C = 1800- (
C = 1800- (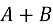 ),
),  = 900-
= 900- 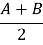 =
=  .
.
- За теоремою синусів знайдемо а і с .
![]() =
= ![]() , a=
, a=![]() ,
,
![]() =
= ![]() , c =
, c =![]() =m + n ,
=m + n ,
![]() = 1800- (A +
= 1800- (A + ![]() ) = 1800- (A +900 -
) = 1800- (A +900 -![]() ) =1800- (A +900 -
) =1800- (A +900 -![]() ) =
) =
= 1800- (![]() ) = 900 -
) = 900 - ![]() .
.
4 . ![]() =
= ![]() ,
, ![]() =
= 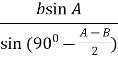 =
= 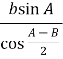 .
.
5 . ![]() =
= ![]() , m =
, m = ![]() =
= 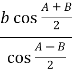 ,
,
![]() =
= ![]() , n =
, n = ![]() =
= 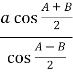 .
.
ЗАДАЧА 19. У трикутнику відомі три сторони a, b ,c. Знайти
медіани ma, mb, mc .
Розв’язання
За наслідком теореми косинусів ![]() = 2 (a2 + b2).
= 2 (a2 + b2).
Діагоналі точкою перетину діляться пополам. Нехай d2 =c, ( с – третя сторона трикутника). Тоді d1 – медіана проведена до сторони с .
Визначимо d1 .
![]() = 2 (a2 + b2) – с2,
= 2 (a2 + b2) – с2,
d1 = ![]() ,
,
mc = ![]() d1 =
d1 = ![]()
![]() .
.
Аналогічно:
ma = ![]()
![]() ,
,
mb = ![]()
![]() .
.
ЗАДАЧА 20. У трикутнику відомо три медіани. Знайти сторони
трикутника.
Розв’язання
Відомо, що кожну медіану можна виразити через сторони трикутника.
Тоді
(2 mc)2= 2 (a2 + b2) – с2, або
4 mc2= 2 a2 + 2b2 – с2, анологічнo
4 ma2= 2 b2 + 2c2 – a2,
4 mb2= 2 a2 + 2c2 – b2,
![]()
![]()
![]() 2 a2 + 2b2 – с2=4 mc2 , 2 a2 + 2b2 – с2=4 mc2 ,
2 a2 + 2b2 – с2=4 mc2 , 2 a2 + 2b2 – с2=4 mc2 ,
2 b2 + 2c2 – a2=4 ma2 , 2 a2 – b2+ 2c2 =4 mb2 ,
2 a2 + 2c2 – b2=4 mb2 , – a2 +2 b2 + 2c2 =4 ma2 ,
Знайдемо визначник ![]() , складений з коефіцієнтів при а2 ,b2,c2
, складений з коефіцієнтів при а2 ,b2,c2
![]()
![]()
![]() =
= 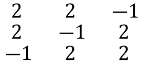 = (-4-4-4) – (-1+8+8) = -12-15 = -27.
= (-4-4-4) – (-1+8+8) = -12-15 = -27.
Замінимо І стовпець на вільні члени.
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1 =
1 = 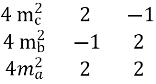 =
= ![]()
![]() -
- ![]() +
+
![]()
![]()
![]()
![]() == -24 mc2 - 24 mb2+ 12 ma2;
== -24 mc2 - 24 mb2+ 12 ma2;
a2 = ![]() =
= ![]() (24 mc2 + 24 mb2- 12 ma2) ;
(24 mc2 + 24 mb2- 12 ma2) ;
a= ![]() .
.
![]()
![]()
![]() 2 =
2 = 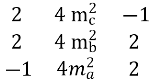 = -
= -![]()
![]() +
+ ![]()
![]() –
–
-
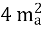
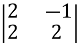 = - 12(2 mc2 + 2 ma2- mb2) ;
= - 12(2 mc2 + 2 ma2- mb2) ;
b2 = ![]() =
= ![]() (2 mc2 + 2 ma2- mb2) ;
(2 mc2 + 2 ma2- mb2) ;
b = ![]() .
.
![]()
![]()
![]() 3 =
3 = 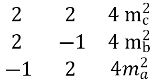 =
= ![]()
![]() -
- ![]()
![]() +
+ ![]()
![]()
= -12(2 ma2 + 2 mb2- mc2) ;
c2 = ![]() =
= ![]() (2 ma2 + 2 mb2- mc2) ;
(2 ma2 + 2 mb2- mc2) ;
c= ![]() .
.
ЗАДАЧА 20. У трикутнику відомі три висоти ha , hb, hc проведені
відповідно до сторін трикутника a,b,c . Знайти сторони
трикутника.
Розв’язання

![]()
 Точка О – ортоцентр. Відомо, що
Точка О – ортоцентр. Відомо, що
![]() =
= ![]() =
= ![]() =
=![]() . По іншому
. По іншому
![]()
2S = ![]() =
= ![]() =
= ![]() .
.
Побудуємо ![]() A1B1C1 зі сторонами а1 =
A1B1C1 зі сторонами а1 =![]() , b1 =
, b1 = ![]() , с1=
, с1=![]() .
.
Цей трикутник буде подібний трикутнику АВС. Отже, відомий і півпериметр
Р1 =![]() ( а1+b1 +c1) =
( а1+b1 +c1) =![]() +
+![]() +
+![]() ).
).
Знайдемо кути ![]() A1B1C1 за задачею 15 (а)
A1B1C1 за задачею 15 (а)
tg ![]() =
= 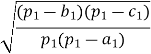 ; tg
; tg ![]() =
= 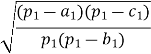 ;
;
tg ![]() =
= 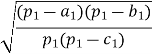 ; C1 =C =2arctg
; C1 =C =2arctg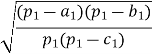 .
.
Знаючи кути і висоти знайдемо сторони а, b і с .
a= ![]() =
=  .
.
Аналогічно шукаються b і с.
ЗАДАЧА 21. У трикутнику дано два гострі кути А і В і площу S
трикутника. Знайти сторони трикутника.
Розв’язання
S = ![]() ab
ab![]() =
= ![]() ac
ac![]() =
= ![]() bc
bc![]() S =
S = ![]() ab
ab![]() , тоді
, тоді
аb = ![]()
і відомо, що ![]() =
= ![]() .
.
Складемо систему і розв’яжемо її.
![]() a=
a= ![]() ,
,
![]() b
b![]() =
= ![]()
![]() b2 =
b2 =![]()
a = ![]() ,
,
b = ![]() , a =
, a = ![]() =
=![]() ,
,
c = ![]() =
=![]()
ЗАДАЧА 22. Знайти радіус зовнішньо – вписаного у трикутник кола,
якщо відомі три сторони трикутника a,b,c.
Розв’язання
-



 Центр кола О належить бісектрисі АО і ОС1=ОВ1=R,
Центр кола О належить бісектрисі АО і ОС1=ОВ1=R,
![]()
![]() R
R![]() AC1 ( радіус завжди перпендикулярний до дотичної ).
AC1 ( радіус завжди перпендикулярний до дотичної ).
- За теоремою косинусів знайдемо кут А
![]() =
= ![]() ,
, ![]() C1AO =
C1AO = ![]() .
.
- CD = CC1 , BD = BB1 ,як дотичні , що виходять з однієї точки.
Тоді AC1 + AB1 = AC + AB + BC = a+b+c.
AC1 = AB1 ,
AC1=![]() = p .
= p .
4 . У прямокутному трикутрику АС1О знайдемо ОС1=R.
OC1 = AC1tg![]() , R = p tg
, R = p tg![]()
РОЗДІЛ ІV
Подібні трикутники
ЗАДАЧА 23. Написати дев’ять відношень у випадку, коли дві
паралельні прямі перетинаються іншими прямими, що
перетинаються у точці М
а) М – зовнішня точка;
б) М – внутрішня точка.
Розв’язання
Випадок( а).
-
 Побудуємо пряму паралельну прямій АМ , що проходить через точку В1 . Утвориться три подібних трикутники:
Побудуємо пряму паралельну прямій АМ , що проходить через точку В1 . Утвориться три подібних трикутники:
![]()
![]()
![]() В1ВС
В1ВС ![]() МВ1А1
МВ1А1 ![]()
![]() МВА ( за ІІ ознакою подібності )
МВА ( за ІІ ознакою подібності )
- Проти рівних кутів лежать пропорційні сторони.
Великий трикутник і середній:
![]() =
= ![]() =
= ![]() ;
;
Великий трикутник і середній:
![]() =
= ![]() =
= ![]() ;
;
Малий трикутник і середній:
![]() =
= ![]() =
= ![]() ;
;
Випадок ( б)

![]()
![]()
![]() СМВ
СМВ ![]()
![]() DМА і
DМА і ![]() DМА
DМА ![]()
![]() D 1ВА ( випадок (а)). Складаємо відношення сторін:
D 1ВА ( випадок (а)). Складаємо відношення сторін:
- Малого трикутника до середнього:
МС лежить проти ![]() СВМ , МD – проти
СВМ , МD – проти ![]() DAМ.
DAМ.
![]() =
= ![]() =
= ![]() ;
;
- малого трикутника до великого :
![]() =
= ![]() =
= ![]() ↔
↔ ![]() =
= ![]() =
= ![]() ;
;
- середнього трикутника до великого:
![]() =
= ![]() =
= ![]() .
.
ЗАДАЧА 24. Дві хорди кола перетинаються у внутрішній точці.
Довести,якщо сполучити кінці хорд, то утвориться два
подібних трикутники.
( інше формулювання задачі )
На колі дано чотири довільних точки. Довести, якщо їх
сполучити попарно, то утвориться дві пари подібних
трикутника.
Доведення

![]()
 Нехай маємо чотири точки кола – A,B,C,D.
Нехай маємо чотири точки кола – A,B,C,D.
- < MDC = <MAB , бо вони спираються на хорду СmB.
- < AMB = < CMD, як вертикальні.
![]()
![]() MDC
MDC ![]()
![]() МBА .
МBА .
-
 Проти рівних кутів лежать пропорційні сторони
Проти рівних кутів лежать пропорційні сторони
![]() =
= ![]() =
= ![]() .
.
Зауваження:
Якщо сполучити AD і ВС, то одержимо два подібні трикутника –
![]() АMD
АMD ![]()
![]() СМB,
СМB,
![]() =
= ![]() =
= ![]() .
.
ЗАДАЧА 25. Дві прямі перетинають коло в точках А,В,С, D і
перетинаються у зовнішній точці М. Довести , що
![]() MАC
MАC ![]()
![]() МDB .
МDB .
Доведення



Обидва трикутники мають спільний кут М.
< BAC = <BDC , бо спираються на дугу BnC , за ІІ ознакою подібності трикутників.
Складаємо відношення відповідних сторін:
![]() =
= ![]() =
= ![]() ↔ MC
↔ MC![]() MD = MA
MD = MA ![]() MB .
MB .
( за даною задачею розв’язуються задачі № ,
за підручником Погорєлова О. В. 7 – 11 кл. )
ЗАДАЧА 26. (№ Геометрія 7 – 11 кл.)
З точки поза колом проведено січну МА і дотичну МС.
Довести , що МС2 = МА![]() МВ.
МВ.
Доведення


Якщо січну MD (задача 25) повертати так, щоб вона стала дотичною , то D і С стягнуться у точку С і з добутку MC![]() MD = MA
MD = MA ![]() MB , маємо:
MB , маємо:
MC![]() MС = MA
MС = MA ![]() MB , МС2 = МА
MB , МС2 = МА![]() МВ.
МВ.
Зауваження: задача 26 використовується при розрахунках на станціях
спостереження, мобільного і телезв’язку, далекість
авіа спостережень.
Наприклад. Відома висота вишки МВ, відомий діаметр Землі АВ.
МС – твірна
конуса , що покриває частину поверхні Землі прямим
радіосигналом (УКВ).
![]()

ЗАДАЧА 27. ( Погорєлов О. В. Геометрія 7 – 11, § 10,№48 )
Довести, що медіани трикутника точкою перетину діляться у
відношенні 2 : 1 починаючи з вершини.
Доведення


![]() Розглянемо
Розглянемо ![]() ANB. М – середина АВ. Через
ANB. М – середина АВ. Через
 М проведемо пряму паралельну AN
М проведемо пряму паралельну AN
![]() ( теорема Фалеса).
( теорема Фалеса).
Середня лінія МР ділить кожний відрізок
![]() пополам, що проведений з вершини
пополам, що проведений з вершини
кута до сторони трикутника .
Тоді BQ = QO. KL –середня лінія трикутника ANC.
На стороні ВС : BP = PN = NL = LC.
Тоді BQ = QO= OK.
Отже, ![]() =
= ![]() .
.
ЗАДАЧА 28. Дано правильний многокутник. Відомі n і сторона
многокутника а .
Знайти радіус описаного кола R і вписаного кола r
через a і n.
Розвязання
-



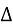 А1ОА2 – рівнобедрений , так як утворений двома радіусами ОА1 = ОА2 = R . < А1ОА2 =
А1ОА2 – рівнобедрений , так як утворений двома радіусами ОА1 = ОА2 = R . < А1ОА2 = 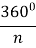 .
.
![]()
![]() - середина А1А2 , А1М= А2М =
- середина А1А2 , А1М= А2М = ![]() а .
а .
![]() ⊥ А1А2 → OM = r, < А1ОM =
⊥ А1А2 → OM = r, < А1ОM = ![]() =
=![]() .
.
-
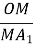 = ctg
= ctg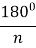 , OM = r =
, OM = r =  ctg
ctg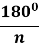 .
.
3 . ![]() = sin
= sin![]() , ОА1 = R =
, ОА1 = R = 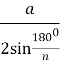 .
.
4 . ![]() = cos
= cos ![]() , r = R cos
, r = R cos ![]() .
.
Зауваження:
Площа ![]() А1ОА = ОМ
А1ОА = ОМ![]() А1М .
А1М .
![]() =
=![]() ctg
ctg![]()
![]() =
= ![]() ctg
ctg![]() .
.
Для многокутника загальна площа: S = n![]() =
= ![]() ctg
ctg![]() .
.
РОЗДІЛ V
Приклади розв’язування трикутників
1. Рівнобедрені трикутники
ЗАДАЧА 1 .Основа рівнобедреного трикутника 30 см, бічні сторони – по 45 см. До
бічних сторін проведені бісектриси. Знайти відрізок , що сполучає основи
бісектрис.

![]() Розв’язання
Розв’язання
-
BD = DC =
 BC = 15 см.
BC = 15 см.
![]()



![]()
![]() Фігура BMNC – трапеція. CM = BN і є діагоналями трапеції, а якщо діагональ є бісектрисою гострого кута , то бічні сторони дорівнюють верхній основі. BM = MN = NC.
Фігура BMNC – трапеція. CM = BN і є діагоналями трапеції, а якщо діагональ є бісектрисою гострого кута , то бічні сторони дорівнюють верхній основі. BM = MN = NC.
- У ∆ ABD визначимо кут В:
![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() .
.
- З точок M і N опустимо перпендикуляри. Вони відтинають відрізки
KL = MN , BK = LC = x.
BC = MN + 2x, 30 = MN + 2x,
X =![]() .
.
-
У ∆ BMK :
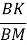 =
= 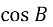 ,
, 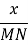 =
= ,
,
![]() =
=![]() ,
, ![]() =
= ![]() , 90 – 3 MN = 2 MN , 90 = 5 MN , MN = 18 см.
, 90 – 3 MN = 2 MN , 90 = 5 MN , MN = 18 см.
Відповідь : 18 см.
ЗАДАЧА 2.( за задачею 19, 20)
У рівнобедреному трикутнику медіана, проведена до
основи, дорівнює 16 см, а до бічної сторони - 2![]() см.
см.
Знайти периметр трикутника.
Розв’язання
Нехай основа - а , бічні сторони – b. Медіани до бічних сторін – рівні.
За задачею 19, 20 , маємо:
-
b =
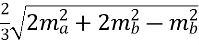 =
= 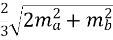 =
= 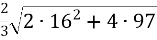 =
=
= ![]() =
= ![]() =
= ![]() = 20 см;
= 20 см;
-
a =
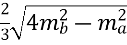 =
= 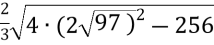 =
= 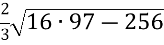 =
=
=![]() =
= ![]() =24 см;
=24 см;
-
Р = 2b+a = 2
 20 + 24 = 64 см.
20 + 24 = 64 см.
Відповідь : 64 см.
ЗАДАЧА 3. ( за задачею 20)
У рівнобедреному трикутнику висота . проведена до
основи дорівнює 20 см, а до бічних сторін – 24 см.
Обчислити периметр трикутника.
Розв’язання
- Нехай основа – а см, бічна сторона – b см.
Р1= ![]() +
+![]() = 20 + 2
= 20 + 2![]() 24 = 68 см;
24 = 68 см;
-
tg
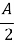 =
= 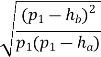 =
= =
= 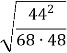 =
= 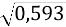 = 0, 77;
= 0, 77;
![]() =
= 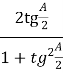 =
= ![]() =
= ![]() = 0,966;
= 0,966; ![]() A=
A=![]() C
C
a = ![]() =
= ![]()
![]() 25 см;
25 см;
-
tg
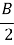 =
= 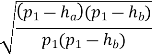 =
=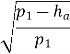 =
= 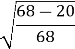 =
= 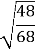 = 0,84;
= 0,84;
![]() =
= 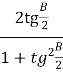 =
= ![]() =
=![]() = 0,984;
= 0,984;
b= ![]() =
= ![]() 20,3 см;
20,3 см;
Отже, Р= 25 + 2![]() 20,3 = 65,6 см.
20,3 = 65,6 см.
Відповідь: 65,6 см.
ЗАДАЧА 4. (за задачею 10)

![]() У рівнобедреному трикутнику точка перетину серединних
У рівнобедреному трикутнику точка перетину серединних
перпендикулярів віддалена від основи на 21 см. Довжина
описаного кола - 150![]() см. Обчислити сторони трикутника.
см. Обчислити сторони трикутника.
![]() Розв’язання
Розв’язання
-
 Якщо C = 150
Якщо C = 150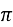 = 2R
= 2R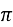 , то R= 75 см;
, то R= 75 см;
- ОК – серединний перпендикуляр до бічної сторони , тоді
OD= 21см, AD= 75 + 21 = 96 см;
- OB = OA = R =75 см.
У![]() OBD : BD =
OBD : BD = ![]() =
=![]() = 72 см,
= 72 см,
ВС = 2![]() 72=144см.
72=144см.
-
У
 АBD : АВ =
АBD : АВ = 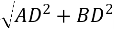 =
= 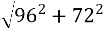 = 120 см.
= 120 см.
Відповідь: 120 см; 144 см; 144 см.
ЗАДАЧА 5. Вершина рівнобедреного трикутника віддалена від точки
перетину бісектриси на 26 см. Довжина вписаного кола –

![]() 20
20 ![]() см. Знайти сторони трикутника.
см. Знайти сторони трикутника.
Розв’язання
-
 За умовою ОВ =26 см, С = 2
За умовою ОВ =26 см, С = 2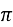 r см, r = 10 см;
r см, r = 10 см;
![]()
![]() BD = BO + OD = 26 + 10 = 36 см;
BD = BO + OD = 26 + 10 = 36 см;
-
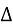 BKO
BKO 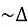 BDA, так як
BDA, так як 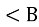 - спільний.
- спільний.
Тоді ![]() =
= ![]() ,
, ![]() =
= ![]() ;
;
-
У
 BDA знайдемо: АВ =
BDA знайдемо: АВ = 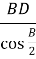 =
= 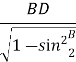 =36:
=36: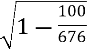 = 36 :
= 36 :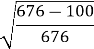 = 36 :
= 36 :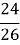 = 39 см.
= 39 см.
AD = ![]() = 15 см, АС = 30 см.
= 15 см, АС = 30 см.
Відповідь: 30 см, 39см, 39 см.
ЗАДАЧА 6. У рівнобедреному трикутнику медіана, проведена до
основи – 25 см. Площа вписаного круга - 64![]() см2. Обчислити
см2. Обчислити
площу і периметр трикутника.
Розв’язання
Малюнок попередньої задачі.
-
Якщо площа круга S =
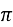 r2 = 64
r2 = 64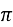 см2 , то r = 8 см.
см2 , то r = 8 см.
- OB = BD – OD= BD – r = 25 – 8 = 17 см.
-
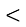 OAD =
OAD = , тоді
, тоді 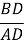 = tg A , a
= tg A , a 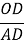 = tg
= tg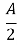 . Але tg A=
. Але tg A= 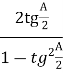 .
.
Виконаємо підстановку.
![]() =
= 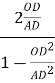 . Нехай AD= x .
. Нехай AD= x .
![]() =
= ![]() ,
, ![]() =
= 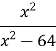 , 25x2 - 25
, 25x2 - 25![]() 64 = 16 x2,
64 = 16 x2,
9 x2 = 25![]() 64,
64,
3x = 40,
X =![]() .
.
-
AC=
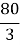 , AB =
, AB = 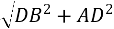 =
= 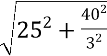 =
= 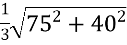 = =
= =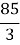 см.
см.
-
S =
 BD
BD AC =
AC =
 25
25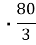
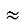 333 см2; P= 2AB + AC
333 см2; P= 2AB + AC 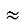 56+ 27
56+ 27 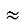 83 см.
83 см.
Відповідь: ![]() 333 см2;
333 см2; ![]() 83 см.
83 см.
ЗАДАЧА 7. Вершина рівнобедреного трикутника віддалена від
точки перетину медіани на 24 см . Довжина вписаного
кола С = 20![]() см. Знайти сторони трикутника.
см. Знайти сторони трикутника.
Розв’язання
-


 АО1= 24 см, OD =10 см. Але точка перетину медіани ділить їх у відношенні 2: 1. Тому
АО1= 24 см, OD =10 см. Але точка перетину медіани ділить їх у відношенні 2: 1. Тому
О1D= 12 см, ОО1= 2 см, висота AD = 36 см.
-
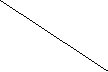 AO = АО1 + ОО1= 24 + 2 = 26 см.
AO = АО1 + ОО1= 24 + 2 = 26 см.
![]()
![]() У
У![]() OKA:
OKA: ![]() =
= ![]() ,
, ![]() =
=![]() =
=![]() .
.
-
У
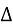 ABD: AB=
ABD: AB= 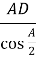 =
=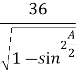 =
=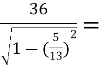 =39 см
=39 см
За задачею 6.
BD = ![]() = 15 см, ВС = 30 см.
= 15 см, ВС = 30 см.
Відповідь : 30 см , 39см , 39см.
ЗАДАЧА 8. Основа рівнобедреного трикутника 36 см, бічна сторона 54
см . До бічних сторін проведені висоти. Обчислити
довжину відрізка , що сполучає основи висот.
Розв’язання
![]()

-
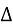 BMC
BMC 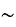
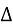 ABD , так як ці трикутники прямокутні і
ABD , так як ці трикутники прямокутні і
![]() В – спільний.
В – спільний.
![]()


![]()
![]() BC = 18 см.
BC = 18 см.
-
BM =
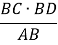 =
= 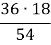 = 12 см.
= 12 см.
- AM = AB – BM = 54 – 12 = 42 см.
Тоді![]() =
= ![]() , OM =
, OM = ![]() =
= ![]() = 14 см.
= 14 см.
-
MN = 2OM = 2
 14 =28 см.
14 =28 см.
Відповідь : 28 см.
ЗАДАЧА 9. У трикутнику АВ = ВС , кути при основі 550. На основі АС
позначено довільні точки E і F починаючи від точки А ,
D![]() AB, C1
AB, C1 ![]() CB. Прямі DF і C1E перетинаються в точці О.
CB. Прямі DF і C1E перетинаються в точці О.
AD + AE = AC. Знайти кут EOF.
Розв’язання
-
 Нехай
Нехай 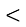 ADF =
ADF = 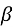 ,
, 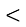 AFD =
AFD = 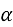 , CE = x , AF = y.
, CE = x , AF = y.
-
У
 ADF : AD = x , AF = y, так як AD=AC – AE=AE+EF+FC- AE= EF+FC= CE
ADF : AD = x , AF = y, так як AD=AC – AE=AE+EF+FC- AE= EF+FC= CE
-
У
 CEC1: CE = x, CC1= y.
CEC1: CE = x, CC1= y.

 Ці трикутники рівні , так як мають по куту 550 і по дві рівні сторони.
Ці трикутники рівні , так як мають по куту 550 і по дві рівні сторони.
у лежить проти кута ![]() , тоді СС1 лежить проти
, тоді СС1 лежить проти
кута ![]() ,
, ![]() С1ЕС =
С1ЕС = ![]() . х лежить проти кута
. х лежить проти кута ![]() .
.
Отже, ![]() ЕС1С =
ЕС1С = ![]() .
. ![]() ЕОF
ЕОF ![]()
![]() АDF
АDF ![]()
![]() EOF = 550.
EOF = 550.
Відповідь: 550.
2. Прямокутні трикутники
ЗАДАЧА 1. ( за задачею 4)
Периметр прямокутного трикутника 60 см, висота, проведена
до гіпотенузи, дорівнює 12 см. Знайти катети.
Розв’язання
-
 h =
h =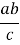 .
.
- За теоремою Піфагора c2 = a2 + b2;
- P = a+b+c.
- Складаємо систему рівнянь і розв’яжемо її .
![]()
![]()
![]()
![]() = 12, 2 ab = 24 c,
= 12, 2 ab = 24 c,
а+b +c= 60, (а+b) +c= 60,
a2 + b2 = c2. a2 + 2ab +b2 = c2 + 24c.
![]() 2 ab = 24 c, Розв’яжемо друге рівняння
2 ab = 24 c, Розв’яжемо друге рівняння
![]() + c = 60, c2 + 24c = ( 60 – с )2,
+ c = 60, c2 + 24c = ( 60 – с )2,
(а+b)2 = c2 + 24c. c2 + 24c = 360 – 120с + с2,
144с = 3600,
С = 25.
Маємо нову систему:
![]()
![]() ab = 12 c, ab = 300,
ab = 12 c, ab = 300,
а+b = 60 – с, а+b = 35,
Це може бути , якщо а = 20, b =15, або навпаки.
Відповідь: 20 см, 15см.
ЗАДАЧА 2. Бісектриса прямого кута дорівнює 12![]() ділить гіпотенузу у
ділить гіпотенузу у
відношенні 3 : 4 . Обчислити периметр трикутника.
Розв’язання
-

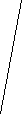 m + n = 3k + 4k = 7k.
m + n = 3k + 4k = 7k.
-
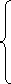 a2 + b2 = 49k2,
a2 + b2 = 49k2,
![]() =
= ![]() ,
,
![]() 2 =ab – mn,
2 =ab – mn,
![]()
![]() 288 = ab – 12 k2, 288 =
288 = ab – 12 k2, 288 =![]() b2 - 12 k2,
b2 - 12 k2,
a2 + b2 = 49k2, ![]() b2+ b2 = 49k2,
b2+ b2 = 49k2,
a = ![]() b,
b,
![]()
![]() 72 =
72 = ![]() - 3k2, b =
- 3k2, b =![]() k,
k,
(![]() b)2 = ( 7k)2. a =
b)2 = ( 7k)2. a =![]() k.
k.
72 = ![]() k2 – 3k2 =
k2 – 3k2 = ![]() k2 ,
k2 , ![]() = k2, k = 5.
= k2, k = 5.
а =28, b= 21, c =35.
P = a + b + с = 28 + 21 + 35 = 84 см.
Відповідь: 84 см.
ЗАДАЧА 3. Катети а і b утворюють пропорцію а : b = 3 : 4.
Різниця R – r = 15 см. Знайти периметр трикутника.
Розв’язання
- Нехай а = 3 k, b =4 k, тоді с= 5 k, так як трикутник зі сторонами 3,4,5 є єгипетський трикутник.
-
Згідно задачі 5, r =
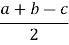 =
=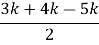 = k.
= k.
-
Але R =
 = 2,5k.
= 2,5k.
R – r =2,5k – k= 15, 1,5k =15, k = 10см.
а = 30см, b= 40см, с = 50см.
Отже, Р= 30 +40 + 50= 120см.
Відповідь: 120 см.
3. Довільні трикутники
ЗАДАЧА 1. У трикутнику основа – 60 см, висота проведена до основи
12 см, медіана – 13см. Знайти периметр трикутника.
Розв’язання
-


 Нехай НМ = х. Тоді х =
Нехай НМ = х. Тоді х =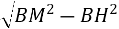 =
=
![]() = 5 см.
= 5 см.
-
AM =
 AC = 30 см, AH = 25 см, CH = 35см.
AC = 30 см, AH = 25 см, CH = 35см.
-
AB =
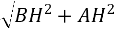 =
=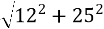 =
=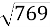
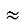
![]() 27,7 см.
27,7 см.
-
BC=
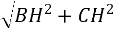 =
= 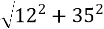 =
= 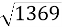 =
=
= 37 см.
P =AB + BC + AC = 27,7+ 37+ 60 = 124,7см.
Відповідь: 124,7 см.
ЗАДАЧА 2. У трикутнику основа 25 см, висота проведена до неї 12 см,
медіана – до основи дорівнює 12,5 см. Обчислити
периметр трикутника.
Розв’язання
-

 АМ= MC= 12,5 см, HM = x. Тоді
АМ= MC= 12,5 см, HM = x. Тоді
 X=
X= ![]() =
=![]() = 3,5 см.
= 3,5 см.
-
AH = 12,5 – 3,5 =9 см, AB=
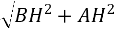 =
=
![]() = 15 см
= 15 см
3 . І спосіб
HC = MC + MH = 12,5 +3,5 = 16 см або AC – AH =25-9 =16 см
BC =![]() =
= ![]() = 20 см.
= 20 см.
ІІ спосіб
Оскільки ВМ= МС= АМ= 12,5 см, то це можливо лише у прямокутному трикутнику з ![]() =900. Тоді 25, 15 і 20 – це сторони єгипетського трикутника, тому ВС = 20 см.
=900. Тоді 25, 15 і 20 – це сторони єгипетського трикутника, тому ВС = 20 см.
4 . Р= АВ + ВС + АС = 15+20+25 = 60 см.
Відповідь: 60см.
ЗАДАЧА 3. ( за задачами 19, 20 )
Одна із сторін трикутника 10 см, а проведені медіани до
інших сторін дорівнюють 9 см і 12 см. Знайти сторони
трикутника.
Розв’язання
- Нехай а = 10 см, mb= 9 см, mc=12 см.
Складаємо відношення сторін і медіан.
![]()
![]() = 2 (a2 +c2) – b2,
= 2 (a2 +c2) – b2,
![]() = 2 (a2 +b2) – c2,
= 2 (a2 +b2) – c2,
- Підставимо числа і розв’яжемо систему рівнянь.
![]()
![]() 4
4![]() 92 =2 (102 +c2) – b2, 4
92 =2 (102 +c2) – b2, 4![]() 81= 200 + 2с2- b2,
81= 200 + 2с2- b2,
4![]() 122= 2 (102 +b2) – c2, 4
122= 2 (102 +b2) – c2, 4![]() 144=200 + 2 b 2- с2,
144=200 + 2 b 2- с2,
![]() 8
8![]() 81 = 400 + 4с2- 2 b 2,
81 = 400 + 4с2- 2 b 2,
8![]() 72 = 200 - с2+ 2 b 2,
72 = 200 - с2+ 2 b 2,
8 ( 81 + 72) = 600+3с2, Знайдемо b
8![]() 153 - 3
153 - 3![]() 200 =3с2, 4
200 =3с2, 4![]() 81 – 200 - 2
81 – 200 - 2![]() 208 = - b 2,
208 = - b 2,
8![]() 51 – 200 = с2, 616 – 324 = b 2,
51 – 200 = с2, 616 – 324 = b 2,
408 – 200 = с2, 292 = b 2,
с2= 208, b ![]() 17
17
с = ![]()
![]() 14,4
14,4
Відповідь: а = 10см, b= 17см, с = 14,4 см.
ЗАДАЧА 4. (за задачею 20)
Медіани трикутника дорівнюють mа =18см, mb=24см,
mc=30см. Знайти площу трикутника.
Розв’язання
-
а =
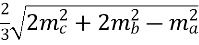 =
= 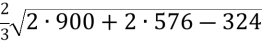 = 34 см
= 34 см
b = ![]() =
= ![]() =29 см
=29 см
c = ![]() =
= ![]() = 20см
= 20см
-
p=
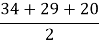 =41,5 см
=41,5 см
-
S =
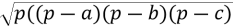 =
= 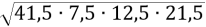
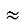 289 см2
289 см2
Відповідь: ![]() 289 см2.
289 см2.
ЗАДАЧА5. У трикутнику бічні сторони 75 см і 78 см, а висота до основи –
72 см. Обчислити відрізки на які ділить бісектриса третю
сторону.
Розв’язання
![]()
![]()
 За умовою : АВ = с = 75 см; ВС = а = 78 см;
За умовою : АВ = с = 75 см; ВС = а = 78 см;
BH = h = 72см; AL = m ; CL = n.
- Нехай HL = x, тоді AH =m-x, m = AH +x,
CH =n+x, n= CH – x.
- Бісектриса ділить протилежну сторону на пропорційні відрізки (наслідок теореми синусів)
![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
3 . Знайдемо за теоремою Піфагора AH і HC.
AH = ![]() =
=![]() = 21 см;
= 21 см;
HC = ![]() =
=![]() = 30 см;
= 30 см;
4 . m =21 + x, n = 30 – x. Тоді ![]() =
= ![]() ,
,
75![]() 30 - 75
30 - 75![]() x = 78
x = 78![]() 21 + 78
21 + 78![]() x,
x,
2250 – 1638 = 153x,
X =4.
Отже, m=25 см , n=26см.
Відповідь: 25см , 26см.


про публікацію авторської розробки
Додати розробку
