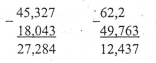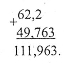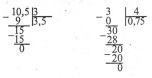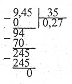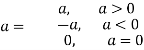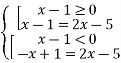Брошурка з алгебри длі підготовки до ДПА/ЗНО
АЛГЕБРА
- ОЗНАКИ ПОДІЛЬНОСТІ ЧИСЕЛ
- ДІЙСНІ ЧИСЛА
![]()
Дійсні числа R
![]()
![]()

![]()
|
Число на яке ділимо |
Ознака |
Приклад |
|
2 |
Остання цифра числа ділиться на 2 (парна). |
956: 2, оскільки остання цифра 6 (парна); 258968:2, оскільки остання цифра 8 (парна). |
|
5 |
Остання цифра числа дорівнює 0 або 5. |
375: 5; 8500: 5 |
|
10 |
Число закінчується на 0 |
5000:10; 2480:10 |
|
4 |
Число, виражене двома останніми цифрами даного числа, ділиться на 4. |
35 724: 4, оскільки 24: 4 |
|
8 |
Число, виражене трьома останніми цифрами даного числа, ділиться на 8. |
17 328: 8, оскільки 328: 8 |
|
3 |
Сума цифр числа ділиться на 3. |
9822: 3, оскільки 9 + 8 + 2 + 2 = 21: 3 |
|
9 |
Сума цифр числа ділиться на 9. |
15 732: 9, бо 1 + 5 + 7 + 3 + 2 = 18: 9 |
Раціональні числа Q Ірраціональні числа
(які можна представити у вигляді дробу) (![]() ,
, ![]() ,
, ![]() )
)
![]()
![]()


Цілі числа Z Дробові числа

![]()
![]() (1/2, 2/7, 3/10…)
(1/2, 2/7, 3/10…)
 Натуральні числа Нуль і цілі від’ємні числа
Натуральні числа Нуль і цілі від’ємні числа
(1,2,3,4…) (-![]() …-2,-1,0,1,2,…+
…-2,-1,0,1,2,…+![]() )
)
- ПРАВИЛА ДІЙ З ЧИСЛАМИ
|
3-5=-2 |
-5+5=0 |
0*5=0 |
Будь-яке число помножене на 0, буде 0! |
|
-3-5=-(3+5)=-8 |
0-5=-5 |
0/5=0 |
Нуль розділити на будь-яке число, буде 0! |
|
-3+5=5-3=2 |
5-0=0 |
|
На нуль ділити не можна! |
|
3+(-5)=3-5=-2 |
3-(-5)=3+5=8 |
5*1=5 |
Будь-яке число помножене на 1, буде теж саме число! |
|
-3+(-5)=-3-5=-8 |
-5*3=-15 |
-6/3=-2 |
При множенні чи діленні двох від’ємних чисел, отримують додатне! |
|
-5+3=-(5-3)=-2 |
-5*(-3)=15 |
-6/(-3)=2 |
|
- ОСНОВНІ ЗАКОНИ АЛГЕБРИ
|
Властивості додавання |
Властивості множення |
|
a + b = b + a; a + (b + c) = (a + b) + c; а + 0 = а; а + (–а) = 0; |
a
a
а
a |
|
Множення одночлена на многочлен |
Множення многочлена на многочлен |
|
|
|
- ДЕСЯТКОВІ ДРОБИ ТА ДІЇ НАД НИМИ
|
Дія |
Правило |
Приклад |
|
Щоб додати чи відняти десяткові дроби, треба записати їх так, щоб кома була під комою і виконати дію. Якщо необхідно, то можна дописати до одного з дробів нулі праворуч. |
|
|
Множать десяткові дроби, не зважаючи на коми, а в добутку виділяють комою праворуч стільки цифр, скільки їх після коми в обох множниках разом. |
|
|
Щоб поділити на десятковий дріб, треба в діленому і дільнику перенести кому вправо на стільки знаків, скільки їх є в дільнику, а потім виконати ділення на натуральне число |
|
- ЗВИЧАЙНІ ДРОБИ ТА ДІЇ НАД НИМИ
|
Дія |
Правило |
Приклад |
|
а) з однаковими знаменниками
б) з різними знаменниками
|
|
|
|
|
|
|
|
|
|
|
- МОДУЛЬ ЧИСЛА
|
Означення |
|
Приклад |
|
Модулем додатного числа називают само це число, модулем від’ємного числа називають число, йому протилежне; модуль нуля дорівнює нулю: |
|
|
- ВІДСОТКИ
|
Означення |
Основні задачі на відсотки |
Приклад |
|
Відсоток – це сота часина цілого |
р% від числа а дорівнює:
|
7% від числа 300 дорівнює:
|
|
|
2. Знаходження числа за заданою величиною його відсотка.
Якщо р% якого-небудь числа становить b, то все число дорівнює |
Число, 30% якого дорівнює 24:
|
|
|
3. Знаходження відсоткового відношення двох чисел.
Число а від числа b становить |
Число 26 від числа 65 становить:
|
- ПРОПОРЦІЯ
|
Означення |
Основна властивість пропорції |
|
Пропорція – це рівність двох відношень
|
|
- ФОРМУЛИ СКОРОЧЕННОГО МНОЖЕННЯ
|
1 |
|
Різниця квадратів |
|
2 |
|
Квадрат різниці |
|
3 |
|
Квадрат суми |
|
4 |
|
Різниця кубів |
|
5 |
|
Сума кубів |
|
6 |
|
Куб різниці |
|
7 |
|
Куб суми |
|
|
|
Розкладання квадратного тричлена на лінійні множники |
- ВЛАСТИВОСТІ СТЕПЕНІВ І КОРЕНЯ n- го СТЕПЕНЯ
|
Властивості степенів |
Приклад |
Властивості кореня n-го степеня |
Приклад |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- РІВНЯННЯ
|
Види рівнянь |
Спосіб розв’язання |
Приклад |
|
|
|
|
|
1. Лінійні рівняння
|
Невідомі доданки перенести вліво, а відомі вправо.
|
Відповідь: 4. |
|
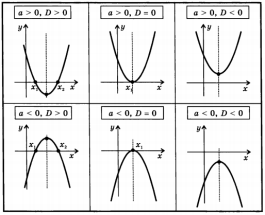
2.Квадратні рівняння
|
Розв’язують за допомогою дискримінанта
Якщо
Якщо
Якщо Або за теоремою Вієта:
|
Відповідь: |
|
3.Рівняння з модулями |
Способи розв’язання:
Якщо
|
Відповідь: -1; 4
2)
Відповідь:4.
3)
Відповідь: - |
|
4.Дробово- раціональні рівняння |
Спосіб розв’язання:
|
Відповідь: -2,2; 6. |
|
5.Ірраціональні рівняння –
це рівняння, в яких невідоме міститься під знаком кореня. |
Способи розв’язання:
При піднесенні обох частин рівняння до парного степеня слід обов’язково робити перевірку одержаних коренів. |
Перевірка:
Відповідь:
|
|
6.Показникові рівняння –
це рівняння, яке містить невідоме в показнику степеня. |
Зведення обох частин до однієї основи є одним з основних методів розв’язання показникових рівнянь.
Способи розв’язання найпростіших показникових рівнянь:
де
де Способи розв’язання показникових рівнянь:
|
1)
2)
3)
4)
Оскільки
5)
Відповідь: 2;3.
6)
Відповідь: 1.
7)
Нехай
Відповідь: 1.
|
|
7.Логарифмічні рівняння –
це рівняння, яке містить невідоме під знаком логарифма. |
Способи розв’язання найпростіших логарифмічних рівнянь:
1. Рівняння виду
де
2. Рівняння виду Способи розв’язання логарифмічних рівнянь:
2.Введення нової змінної.
|
Відповідь: 4.
Нехай
Відповідь: 16;
|
|
8.Тригонометричні рівняння –
це рівняння, яке містить невідоме під знаком тригонометричної функції. |
1)
Якщо
Якщо рівняння розв’язків не має. Окремі випадки
Якщо
Якщо рівняння розв’язків не має. Окремі випадки
4)
|
1.
2.
3.
|
- НЕРІВНОСТІ
|
Строгі нерівності |
Нестрогі нерівності |
|
Дужки круглі () Точка виколота |
Дужки квадратні [] Точка замальована |
|
Види нерівностей |
Спосіб розв’язання |
Приклад |
|
Лінійні нерівності
|
Невідомі доданки перенести вліво, а відомі вправо.
|
Відповідь:
|
|
Квадратні нерівності
|
Метод інтервалів
|
-2 7
Відповідь:
|
|
Метод інтервалів |
|
|
|
- ТРИГОНОМЕТРІЯ
|
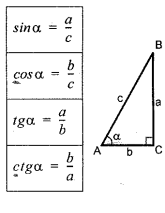
Означення тригонометричних функцій через прямокутний трикутник |
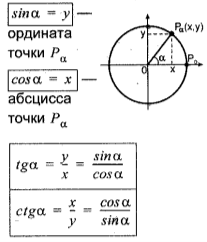
Означення тригонометричних функцій через одиничне коло |
|
|
|
Значення деяких кутів тригонометричних функцій
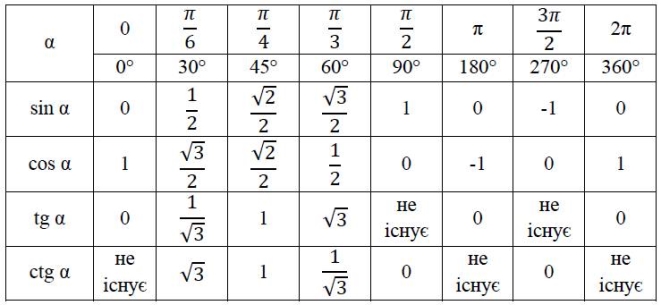
|
|
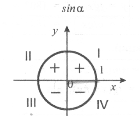
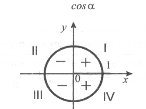
Знаки тригонометричних функцій
|
|
|
|
|
|
Формули зведення

Співвідношення між тригонометричними функціями одного аргументу
|
|
|
|
|
|
|
|
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Формули додавання:
|
|
|
|
|
|
|
|
|
|
|
|
Формули подвійного аргументу:
|
|
|
|
|
|
Формули суми і різниці однойменних тригонометричних функцій
|
|
|
|
|
|
|
|
|
- АРИФМЕТИЧНА ТА ГЕОМЕТРИЧНА ПРОГРЕСІЇ
|
Арифметична прогресія |
Геометрична прогресія |
|
Арифметичною прогресією називається числова послідовність, в якій кожен наступний член, починаючи з другого, дорівнює попередньому члену, до якого додається одне й те саме число. Це число називається різницею прогресії, і позначається d. |
Геометричною прогресією називається числова послідовність, в якій кожен наступний член, починаючи з другого, дорівнює попередньому, помноженому на одне й те саме число. Це число називається знаменником прогресії, і позначається q. |
|
Пишуть. a1, a2, a3, …, an, …. n-ний член арифметичної прогресії обчислюється за формулою: an=a1+d(n-1)
Нариклад у арифметичній прогресії Сума n перших членів арифметичної прогресії:
|
Пишуть. b1, b2, b3, …, bn, …. n-ний член геометричної прогресії обчислюється за формулою: bn=b1qn-1
Нариклад у геометричній прогресії Сума n перших членів геометричної прогресії:
|
- ФУНКЦІЇ
|
Функція – це залежність змінної у від змінної х, коли кожному значенню х відповідає єдине значення у Позначають функції у, у(х), f, f(x) х – незалежна змінна (аргумент) у – залежна змінна (функція) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Властивості функції
Щоб знайти нулі функції, треба функцію прирівняти до нуля
Функція називається монотонною, якщо вона лише зростаюча або лише спадна в своїй області визначення.
Якщо функція зростає, то більшому значенню функції відповідає більше значення аргументу. Якщо функція спадає, то більшому значенню функції відповідає менше значення аргументу.
Якщо f(-х)= f(х), то функція є парною; Якщо f(-х)= -f(х), то функція є непарною; Якщо не виконується ні одна з рівностей, то функція є ні парною, ні непарною.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
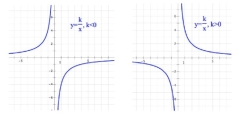
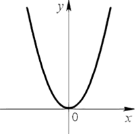
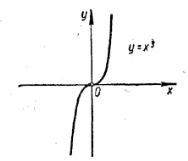
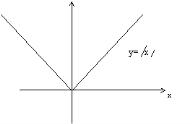
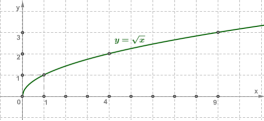
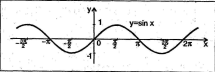
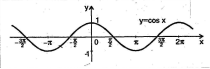
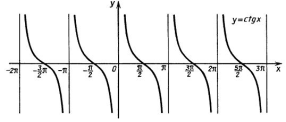
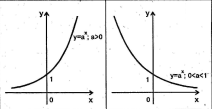
ФУНКЦІЇ, ЇХ ВЛАСТИВОСТІ ТА ГРАФІК
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- ЛОГИРИФМИ
|
Означення |
Властивості |
Приклади |
|
Логарифмом числа
|
|
|
|
|
|
|
|
Наприклад,
|
|
|
|
Види логарифмів:
|
|
|
|
(е=2,7) |
|
|
|
|
|
|
|
|
|
|
|
Основна логарифмічна тотожність |
|
|
- ПОХІДНА ФУНКЦІЇ
|
Правила диференціювання |
Таблиця похідних |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- РІВНЯННЯ ДОТИЧНОЇ
Рівняння дотичної до графіка функції у = f(x), проведена в точці з абсцисою х0, що належить графіку функцій, має вигляд
![]()
- ІНТЕГРАЛ ФУНКЦІЇ
|
Невизначений інтеграл – це множина
Позначається так:
|
Приклади:
|
|
|
Таблиця основних інтегралів |
Властивості невизначеного інтеграла |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
Визначеним інтегралом функції
|
Приклади:
1)
2)
3)
|
- КОМБІНАТОРИКА ТА ТЕОРІЯ ІМОВІРНОСТІ
Імовірністю випадкової події А називається відношення кількості елементарних подій m, які сприяють появі цієї події, до загальної кількості n подій.
Властивості імовірності:1. Імовірність достовірної події дорівнює 1. 2. Імовірність неможливої події дорівнює 0.
3. Імовірність будь-якої випадкової події
|
|
Комбінаторика - це розділ математики, що відповідає на питання скількома способами можна вибрати елементи певної множини, якщо вибірка задовольняє деяким властивостям.
Позначення:
Позначення:
Порядок важливий!!!
Позначення:
Порядок не важливий!!! |

про публікацію авторської розробки
Додати розробку