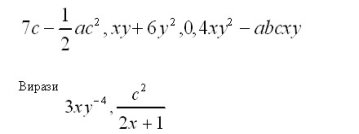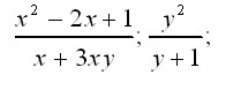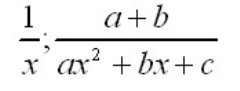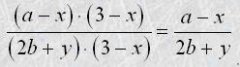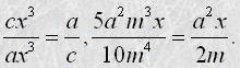Буклет на тему "Раціональні вирази"

Що таке алгебраїчний вираз? Що таке вирази зі змінними?

Якщо з'єднати числа, знаки дій, дужки в одному виразі, то отримаємо числовий вираз. Приклади числових виразів:  

        1+2 ( +) · 15 - 8: 2; ()- 2 ()· 3;

Числовий вираз дорівнює числу, яке ми отримаємо, виконавши всі дії в цьому числовому виразі.

Якщо у виразі крім чисел використовувати букви, то отримаємо буквенний вираз.

Буквеними виразами називають записи, в яких числа і букви з’єднані знаками дій. Наприклад, x-3, x+y, 3a+2b, c:d.

Перетворення виразів:

1. При розкритті дужок, перед якими стоїть "+", цей знак і дужки можна опустити. Наприклад, a+(-b+c+4)=a-b+c+4.

2. Щоб розкрити дужки, перед якими стоїть знак "-", слід опустити дужки і знак "-", змінивши знаки всіх доданків у дужках на протилежні. Наприклад, -(a-b) = -a+b;         x-(-y+z)=x+y-z.

3. Якщо перед дужками стоїть множник, то на нього умножають кожний доданок у дужках. Наприклад, 6+4(a-b) = 6+4a-4b; -4(5-3a) = - 20 +12a.

Доданки, які мають однакову буквену частину, називаютьподібними доданками. Наприклад, 4a і (-5a).

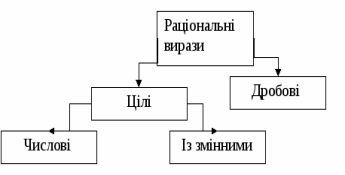
Цілі раціональні вирази. Дробові раціональні вирази

Цілими раціональними виразами називаються числові вирази, а також вирази із змінними, які можуть містити дії додавання,віднімання, множення, піднесення змінних до натурального степеня. Приклади цілих раціональних виразів:

Вирази не є цілими раціональними, бо містять операції піднесення до від'ємного степеня і ділення на змінні.

Дробові раціональні вирази. Основна властивість раціонального дробу

Дробовими раціональними (дробово-раціональними) виразами називають вирази із змінними, які можуть містити операції додавання, віднімання, множення, піднесення змінних до натурального степеня, а також ділення на вирази із змінними. Приклади дробово-раціональних виразів:

Раціональним дробом називається вираз P/Q , де P і Q – раціональні вирази, причому вираз Q обов'язково містить змінні. Приклади раціональних дробів:

Основна властивість дробу

Якщо чисельник і знаменник дробу помножити на один і той самий вираз, то дістанемо дріб, який тотожно дорівнює даному. Наприклад

Основна властивість дробу дає можливість замінити дріб тотожно рівним йому дробом. Таке перетворення називають скороченням дробу . Наприклад

Рацiональнi вирази

Підготувала Сімейко А.І.

Гімназія нових технологій навчання

Кіровоградської міської ради

Кіровоградської області