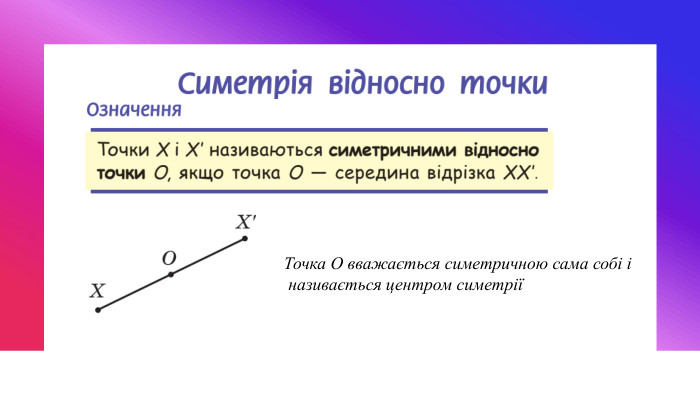
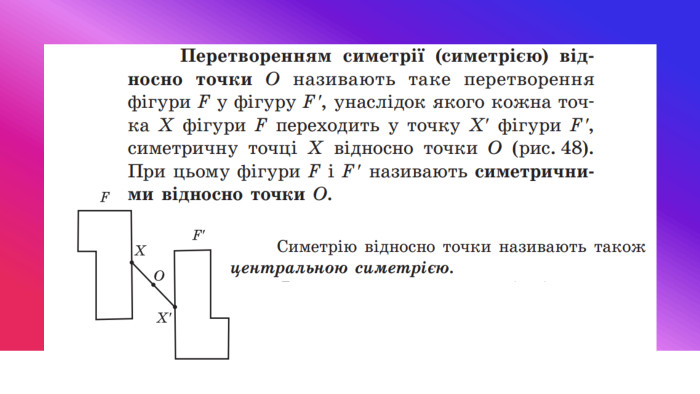
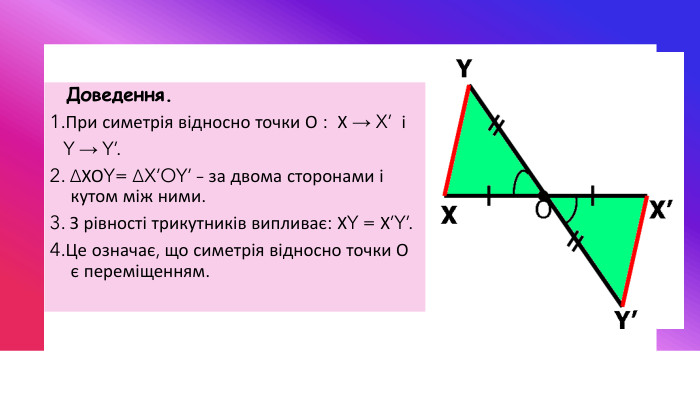
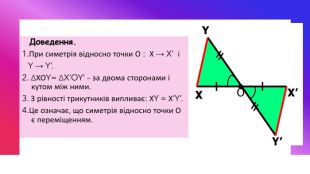
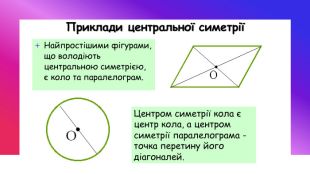
Центральна та осьова симетрія

Про матеріал

Розробка уроку з геометрії на тему "Центральна та осьова симетрія" до підручника Єршова А. П. 2017 рік

Перегляд файлу

Попередній слайд 1 / 9 Наступний слайд

Зміст слайдів

Номер слайду 1

Центральна та осьова симетрія9 клас

Номер слайду 2

Точка О вважається симетричною сама собі і називається центром симетрії

Номер слайду 3

Номер слайду 4

Номер слайду 5

Доведення. 1. При симетрія відносно точки О : Х → X’ і Y → Y’.2. ΔХОY= ΔX’OY’ – за двома сторонами і кутом між ними. 3. З рівності трикутників випливає: ХY = Х’Y’. 4. Це означає, що симетрія відносно точки О є переміщенням.

Номер слайду 6

Приклади центральної симетріїНайпростішими фігурами, що володіють центральною симетрією, є коло та паралелограм. Центром симетрії кола є центр кола, а центром симетрії паралелограма - точка перетину його діагоналей.