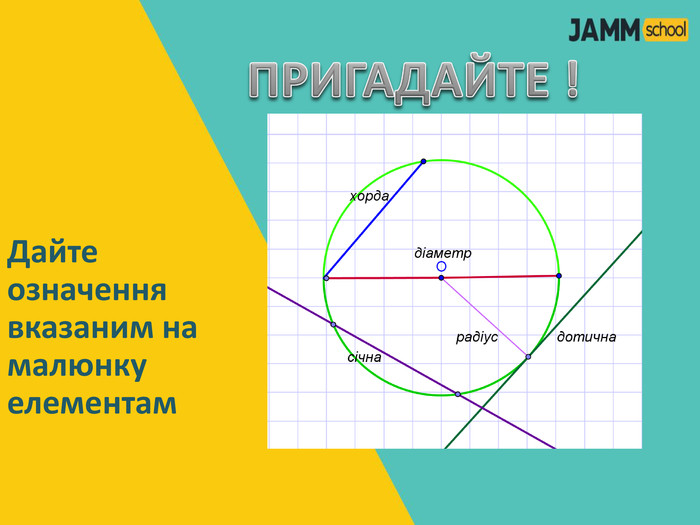
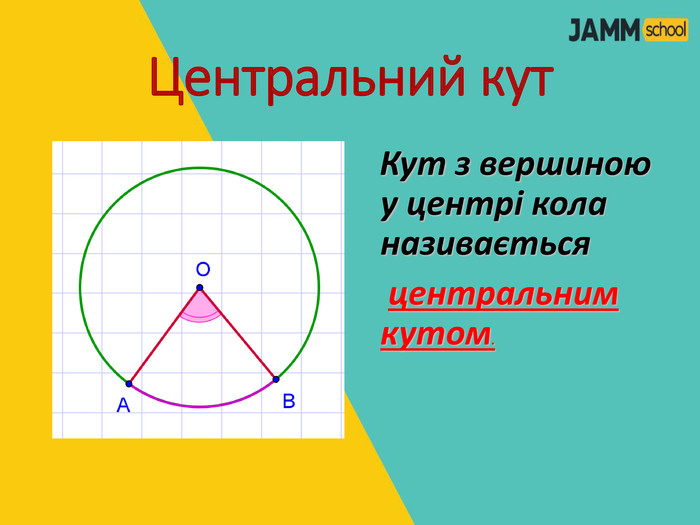
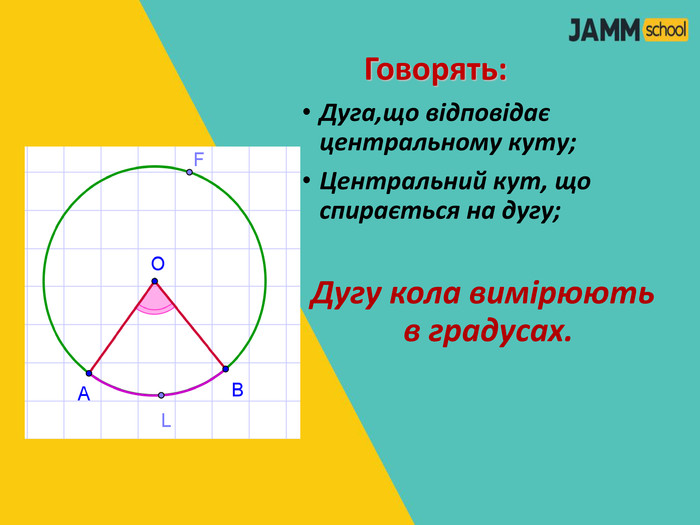
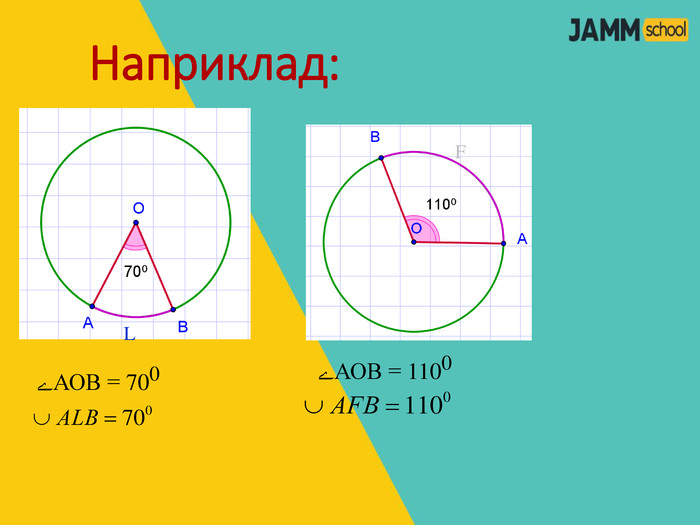
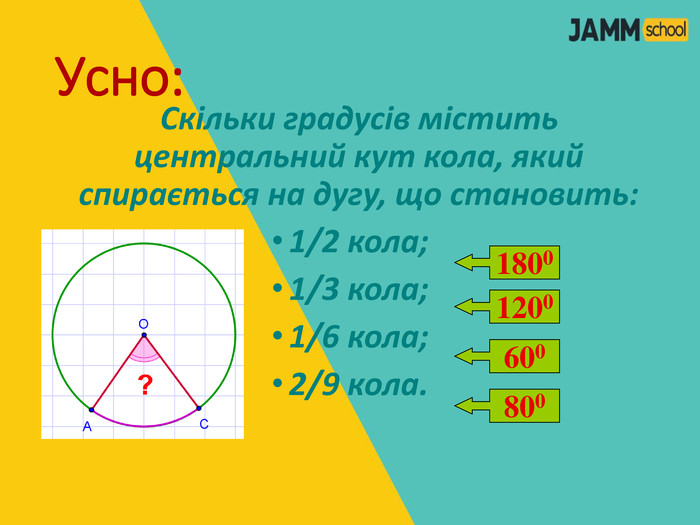
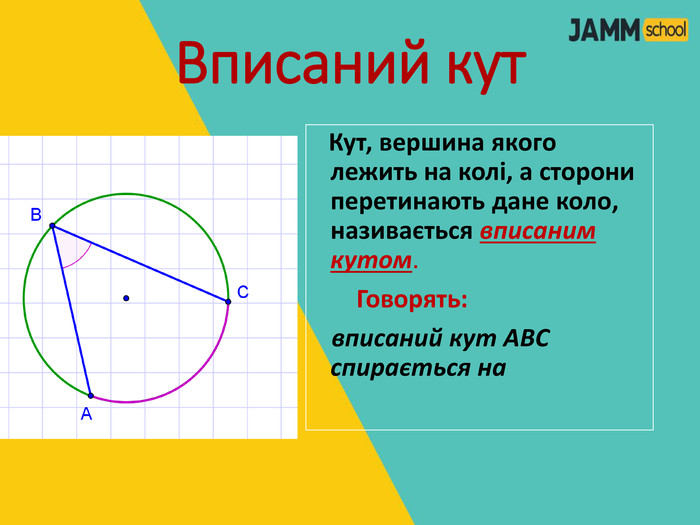
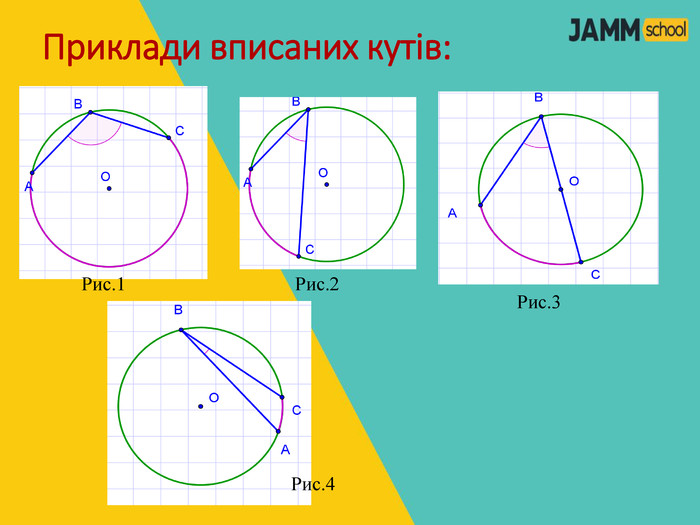
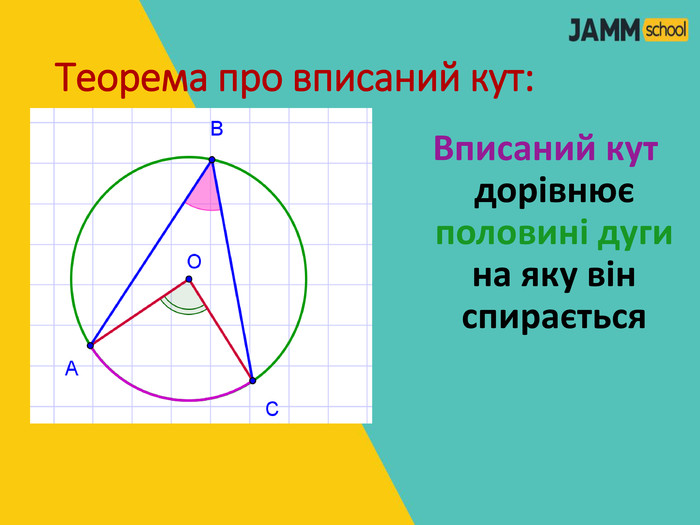
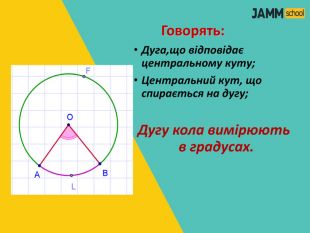
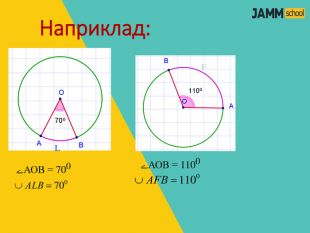
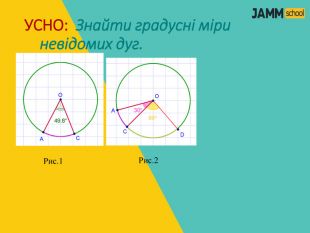
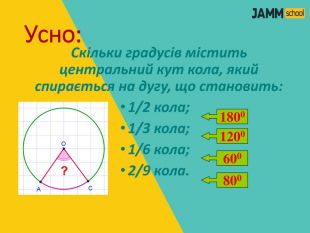
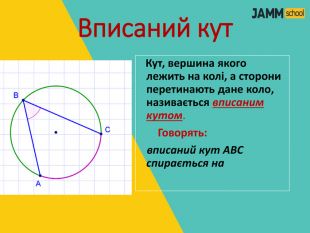
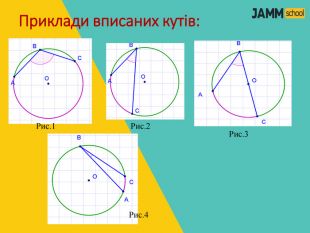
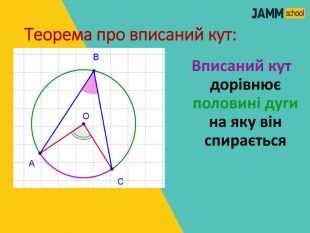
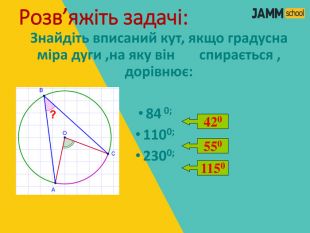
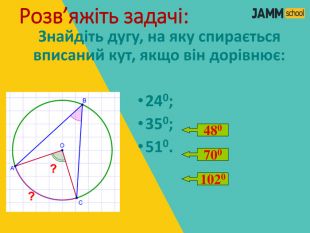
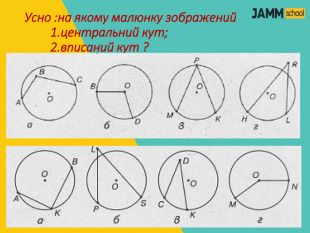
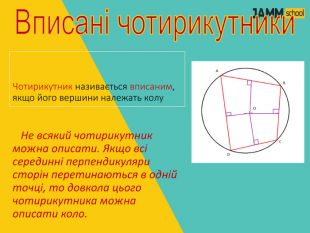
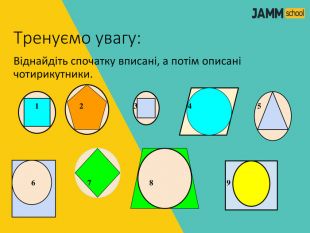
ЦЕНТРАЛЬНІ ТА ВПИСАНІ КУТИ
Про матеріал
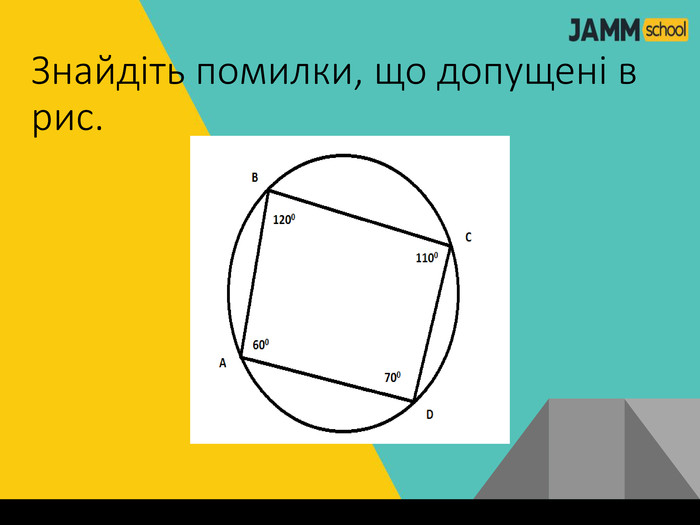
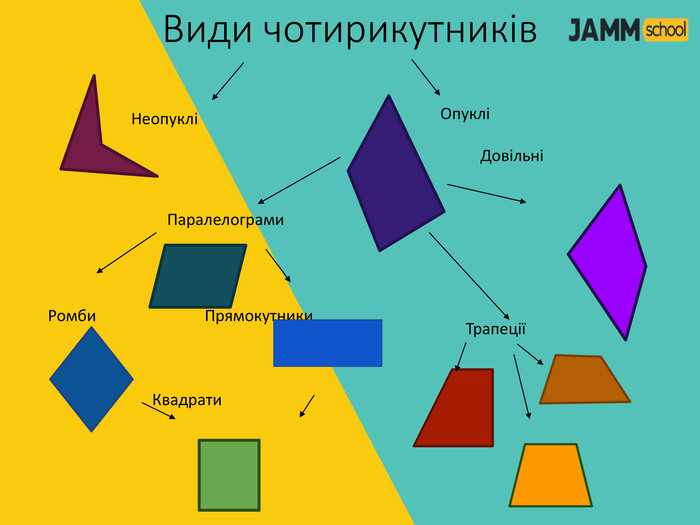
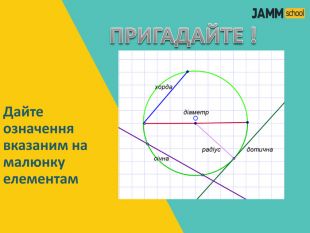
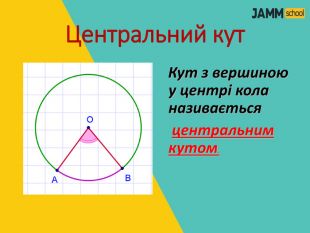
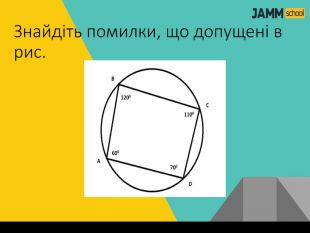
Дана презентація містить пояснення та типові вправи до теми "Центральні та вписані кути. Описаний та вписаний чотирикутник".
Вправа на розвиток уваги та є інтерактивні тести для закріплення теми. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку