Урок "Теорема Піфагора"
ТЕМА УРОКУ: Теорема Піфагора.
Мета уроку:
- сформулювати теорему Піфагора;
- познайомити учнів з біографією Піфагора;
- вчити застосовувати теорему до розв'язання задач;
- розвивати логічне мислення;
- розвивати інтерес до математики.
Тип уроку: урок засвоєння нових знань.
Обладнання: мультимедійний комплекс.
ВСТУП
Вчитель приводить відомі вислови про математику та значимість теореми Піфагора у геометрії (слайд 1):
1. «Математика - знаряддя для мислення, оскільки все, що є в небі, в душі, на землі можна виразити точним числом» (Річард Фейман).
2. «Теорема Піфагора – це головна і найкраща теорема геометрії» (О.Д.Александров).
3. Портрет Піфагора Самоського.
«Природа говорить мовою математики: букви цієї мови — кола, трикутники й інші математичні фігури» (Галілей).
Математика виникла як наука, що допомагає пізнати світ. І теорема Піфагора ще один доказ цього факту.
У 1974 році до сузір’я Геркулес було відправлено потужний радіосигнал, який містив у собі 1679 різних повідомлень про людство, його наукові та культурні надбання, планету Земля, її хімічний склад та розміри. Серед них була зашифрована і теорема Піфагора. Дізнатись про те, чи змогли інші істоти у всесвіті розшифрувати і зрозуміти цю теорему ми зможемо дізнатися лише через 5 тис років (саме через цей проміжок часу повернеться сигнал назад на Землю). А чи зможете зрозуміти її ви, ми дізнаємося вже наприкінці уроку.
І. Організаційний момент
1. Вітання.
2. Тема уроку (слайд 2).
3. Мета уроку (слайд 3).
ІІ. Актуалізація знань учнів
Вчитель пропонує учням відповісти на ряд усних запитань, які допоможуть краще засвоїти новий матеріал
1. Назвіть сторони прямокутного трикутника АВС.
2. Яку із сторін називають гіпотенузою? (АВ, сторона, яка лежить напроти прямого кута).
3. Яку із сторін називаємо катетом? (АС, ВС).
4. Назвіть катет прилеглий до кута А? (b), до кута В? (а).
5. Назвіть катет, протилежний куту А? (а), куту В? (b).

Історична довідка
Презентація про Піфагора
Піфагор народився близько 580 р. до н.е. на острові Самос. Там у сім'ї “золотих діл майстра” народився син. За давньою легендою, молодому подружжю Мнесахера і Парфеніси оракул устами бога Аполона Піфійського пророчив народження сина, який прославиться у віках своєю мудрістю, ділами і красою. Тому, коли народився син, йому дали ім'я Піфагор, тобто передбачений Піфієм.
Піфагор і справді виявив неабиякі здібності до наук. У свого першого вчителя Гермодамаса він вивчив основи музики і живопису. Пам'ять тренував завчаючи пісні “Одіссея” та “Імада”. Зовсім юним він залишив Батьківщину і вирушив до Єгипту. Але до Єгипту ще далеко і він на острові Лесбос у своїх родичів під опікою Фалеса кілька років навчався астрології, передбаченню затемнень, таємниці чисел, медицині, Піфагор відвідав також Вавілон, де він вивчив теорію чисел. Всі ці подорожі сприяли тому, що Піфагор став найосвіченішою людиною свого часу. В 60 років Піфагор повертається на свою батьківщину, де організовує школу, яка діяла майже 30 років.
Школа Піфагора – це заклад зі строго обмеженою кількістью учнів з аристократії і потрапити туди було дуже нелегко. Претендент мав витримати кілька іспитів. Піфагорійці прокидалися зі світанком, співали, акомпануючи собі на мрії, потім робили гімнастику, вивчали теорію музики, філософії, математики, астрономію та інші науки.
Навчання в школі було двоступінчатим. Одні учні називалися “математиками”, тобто пізнавачами, а інші – “акусматиками”, тобто слухачами. Школа була одночасно і філософською і політичною партією і релігійним братством. Наприкінці V століття до н.е. в Греції прокотилася хвиля демократичного руху. Піфагор з учнями переїхав у Тарент, а звідти в Метапонт, де відбулося народне повстання. В одній із нічних сутичок і загинув майже 90 літній Піфагор.
Основна ідея Піфагорійців “Початком усього є числа”. Без них нічого б не було і не було б порядку, гармонії. Піфагорійці приписували числам різні властивості. Парні числа вважалися нещасливими, а непарні – щасливими. Так, вважається, що слід дарувати букет з непарної кількості квіток. Піфагорійці розбили всі числа на непарні – “чоловічі”, і парні “жіночі”. Символ шлюбу складався із суми чоловічого непарного числа 3 і жіночого числа 2, тобто 5. З цієї причини прямокутний трикутник зі сторонами 3, 4, 5 називали фігурою нареченої. Піфагорійці винайшли і досконалі числа, які дорівнювали сумі своїх дільників (крім самого числа). Наприклад 6=1+2+3, або 28=1+2+4+7+14.
Увесь світ, на думку піфагорійців, був побудований на перших чотирьох непарних і перших чотирьох парних числах, а тому найстрашнішою клятвою в них вважалась клятва числом 36. За їх теорією число 666 – це “число звіра”, воно дорівнює сумі квадратів перших семи простих чисел; воно дорівнює сумі перших 36 натуральних чисел і багато іншого. Піфагор пильно вивчав співвідношення чисел і застосував їх у музиці. Піфагорійці дійшли висновку, що якісні відмінності звуків обумовлюються кількісними розходженнями довжин струн. Наприклад, відношення числа коливань у чистої квінти 2:3, у кварті 3:4, октави 1:2. Гармонійний акорд виходить при звучанні трьох струн, коли їхні довжини зіставляються зі співвідношенням чисел 3, 4 і 6.
Трикутник зі сторонами 3, 4, 5 називають також Піфагоровим. Піфагорових трикутників безліч (5; 12; 13), (6; 8; 10), (8; 15; 17), (7; 24; 25) і т.д. Застосування теореми Піфагора разноманітне:
- для вимірювальних робіт (це знали ще в III тис. до н.е.);
- для геометричного знаходження квадратних коренів з цілих чисел;
- для знаходження степенів цілих чисел тощо.
Те, що Піфагор пов'язав реальний світ з числовими закономірностями, дало змогу більш пізнім поколінням учених зрозуміти краще світ і глибше.
ІІІ. Закріплення нових знань і вмінь учнів
Розв'язування задач
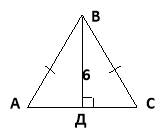 1. Основа рівнобедреного трикутника 16см, а висота, проведена до основи, дорівнює 6см. Знайдіть бічну сторону трикутника.
1. Основа рівнобедреного трикутника 16см, а висота, проведена до основи, дорівнює 6см. Знайдіть бічну сторону трикутника.
Дано: АС – основа, АС = 16см,
ВД – висота, ВД = 6см.
Знайти: АВ.
Розв’язання:
∆АВС – рівнобедрений, ВД – висота.
За властивістю висоти рівнобедреного трикутника ВД – медіана,
АД = ДС = 8см.
∆АВД – прямокутний, за теоремою Піфагора: ![]()
Відповідь: 10 см.
2. Діагональ прямокутника дорівнює 10см, а одна з його сторін 8см. Знайдіть периметр прямокутника.
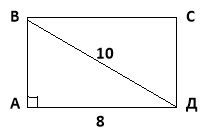 Дано: АВСД – прямокутник, ВД – діагональ,
Дано: АВСД – прямокутник, ВД – діагональ,
ВД = 10см, АД = 8 см.
Знайти: Р.
Розв’язання:
Р = (АВ +ВС)× 2
АВД – прямокутний трикутник, за теоремою Піфагора:
![]() ;
; ![]() ;
;
![]()
Р = (6+8)× 2 = 28(см).
Відповідь: 28см.
3. У прямокутній трапеції АВСД з основами АД і ВС, кут А – прямий, АВ = 4дм. З вершини С до основи АД проведений перпендикуляр СК, КД = 3дм, Знайдіть СД.
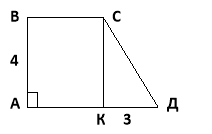 Дано: АВСД – трапеция, <А =
Дано: АВСД – трапеция, <А = ![]() , АВ = 4 дм.
, АВ = 4 дм.
СК ![]() АД , КД = 3 дм.
АД , КД = 3 дм.
Знайти: СД.
Розв’язання:
Оскільки АВСД трапеція: АД//ВС, АВ//СК,
АВ = СК = 4дм.
Розглянемо ∆СДК, <К = 90°.
За теоремою Піфагора: ![]() ;
; ![]() ;
;
![]() .
.
Відповідь: 5дм.
Самостійна робота
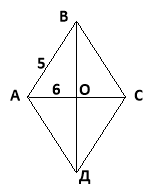 I варіант. Сторона ромба дорівнює 5см, а його менша діагональ 6см. Знайдіть велику діагональ ромба.
I варіант. Сторона ромба дорівнює 5см, а його менша діагональ 6см. Знайдіть велику діагональ ромба.
Розв’язання:
Ми знаємо, що за властивістю діагоналей ромба АС![]() ВД і АО = ОС = 3см.
ВД і АО = ОС = 3см.
Отже ∆АОВ – прямокутний.
За теоремою Піфагора:
АВ²=АО ²+ ВО²,
![]() (см),
(см),
ВД = 2ВО = 8 (см).
Відповідь: 8см.
ІІ варіант. Знайдіть діагональ прямокутника, якщо одна з його сторін дорівнює 8см, а периметр 46см.
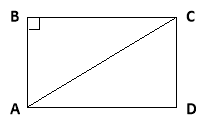 Розв’язання:
Розв’язання:
Р = 46см, АВ + ВС = 46:2 = 23 (см),
АВ = 23 – 8 = 15(см).
∆АВС – прямокутний. За теоремою Піфагора:
АС² = АВ² + ВС²,
![]() .
.
Відповідь: 17см.
Перевірка самостійної роботи. Кожен перевіряє і порівнює свій розв'язок із представленим на слайді, оцінює свою роботу.
V. Рефлексія, домашнє завдання (слайди 13-14).
1. Виставлення оцінок.
2. Цікаві вислови про теорему Піфагора:
- “ Піфагорові штанці файні є у три кінці ”.
- “ Піфагорові штани на всі боки рівні ”.
- “ Хто в сорочці Піфагора – піднось руки вгору ”.
3. Моральні правила Піфагора:
- Роби тільки те, що не засмутить тебе і не примусить розкаюватись.
- Навчись тому, що слід знати.
- Не нехтуй здоров'ям свого тіла.
- Привчайся жити просто і без розкошів.
- Твори велике, не обіцяючи великого.
- Не давай дурневі в руки меч, а нечесному – владу.
4. Домашнє завдання: § 18, № 653, 657, 659, за підручником О. С. Істер – Геометрія, 8 клас.
1


про публікацію авторської розробки
Додати розробку
