2017 рік
Зміст:

Гармонія

Золотий переріз - гармонійна пропорція

Другий золотий переріз

Золотий трикутник

Числа Фібоначчі

Узагальнений золотий переріз

Історія золотого перерізу

Теорема Піфагора і числа Фібоначчі

Золотий кут (137,5 ° ...)

Золотий переріз в живопису

Краса пропорційності

Золотий переріз в архітектурі

Мої дослідження

Висновок

Джерела інформації

 

 

 

 

Гармонія

Числа не управляють світом,

але вони показують,

як управляється світ.

                         Гете

З давніх пір людина прагне оточувати себе гарними речами. Вже предмети побуту жителів старовини, які, здавалося б, переслідували чисто утилітарну мету - служити сховищем води, зброєю на полюванні і т.д., демонструють прагнення людини до краси. На певному етапі свого розвитку людина почала задаватися питанням: чому той чи інший предмет є красивим і що є основою прекрасного? Вже в Стародавній Греції вивчення сутності краси, прекрасного, сформувалося в самостійну гілку науки - естетику, яка в античних філософів була невіддільна від космології. Тоді ж народилося уявлення про те, що основою прекрасного є гармонія.

Краса і гармонія стали найважливішими категоріями пізнання, певною мірою навіть його метою, бо в кінцевому підсумку художник шукає істину у красі, а вчений - красу у правді.

Краса скульптури, краса храму, краса картини, симфонії, поеми ... Що між ними спільного? Хіба можна порівнювати красу храму з красою ноктюрна? Виявляється можна, якщо будуть знайдені єдині критерії прекрасного, якщо будуть відкриті загальні формули краси, об'єднуючі поняття прекрасного самих різних об'єктів - від квітки ромашки до краси оголеного людського тіла?

Існує легенда, що одного разу Будда провів проповідь без єдиного слова. Він просто простягнув квітку своїм парафіянам. Відомий італійський теоретик архітектури Леон-Батіста Альберті, який написав багато книг про зодчество, говорив про гармонію наступне:

"Є щось більше, що складається зі сполучення та зв'язку трьох речей (числа, обмеження і розміщення), щось, чим чудово освітлюється весь лик краси. Це ми називаємо гармонією, яка, без сумніву, джерело всякої принади і краси. Адже призначення і мета гармонії - упорядкувати частини різні за природою досконалим співвідношенням так, щоб вони одна інший відповідали, створюючи красу ... Вона охоплює все життя людське, пронизує всю природу речей. Бо все, що створює природа, підкоряється законам гармонії . І немає у природи більшої турботи, ніж та, щоб створене нею було досконалим".

У Великій Радянській Енциклопедії представлене наступне визначення поняття "Гармонія":

"Гармонія - домірність частин і цілого, злиття різних компонентів об'єкта в єдине органічне ціле. В гармонії отримують зовнішнє виявлення внутрішня впорядкованість і міра буття".

"Формул краси" вже відомо чимало. Вже давно в своїх творіннях люди відтворюють правильні геометричні форми - квадрат, коло, трикутник, піраміду і т.д. В пропорціях споруд надається перевага цілочисловим співвідношенням.

З багатьох пропорцій, якими здавна користувалася людина при створенні гармонійних творів, існує одна, єдина і неповторна, що володіє унікальними властивостями. Цю пропорцію називали по різному - "золотою", "божественною", "золотим перерізом", "золотим числом", "золотою серединою".

"Золота пропорція" - це поняття математичне, та її вивчення – це, перш за все, завдання науки. Але вона є критерієм гармонії і краси, а це вже категорія мистецтва та естетики.

Людина розрізняє предмети, які її оточують, за формою. Інтерес до форми якогось предмету може бути продиктований життєвою необхідністю, а може бути викликаний красою форми. Форма, в основі побудови якої лежить поєднання симетрії і золотого перетину, сприяє найкращому зоровому сприйняттю і появі відчуття краси і гармонії. Ціле завжди складається з частин, частини різної величини знаходяться в певному відношенні один до одного і до цілого. Принцип золотого перерізу - вищий прояв структурної і функціональної досконалості цілого і його частин у мистецтві, науці, техніці і природі.

До 1900-х років термін Phi не застосовувався, поки американський математик Марк Барр не використав грецьку букву φ (phi) для визначення цієї пропорції. До цього часу ця всюдисуща пропорція була відома як золотий розподіл, золотий переріз, золоте співвідношення, а також як Божественна пропорція.

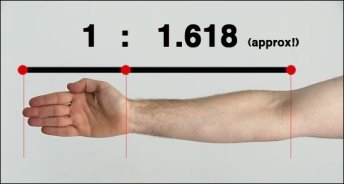
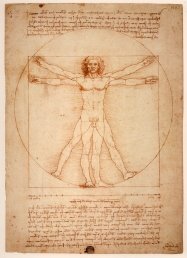
Число 1,618 у математиків називається число Phi (фі), яку можна отримати з послідовності Фібоначчі (математичної прогресії: 1-1-2-3-5-8-13-21 ...) відомою не тільки тим, що сума двох сусідніх чисел в ній дорівнює наступному числу, але й тому, що відношення двох сусідніх чисел володіє унікальною властивістю-наближеністю до числа 1,618, тобто до числа Phi. Незважаючи на містичне походження, число фі зіграло по-своєму унікальну роль. Роль цеглинки у фундаменті побудови всього живого на землі. Всі рослини і навіть людські істоти наділені фізичними пропорціями, приблизно рівними кореню від співвідношення числа фі до 1.Чи відомо вам, що якщо в будь-якому бджолиному вулику розділити число жіночих особин на число чоловічих, то ви завжди отримаєте одне і те ж число- Phi. Леонардо Да Вінчі вивчав людське тіло, і ніхто краще за нього не розумів божественної структури людського тіла, його будови. Він першим показав, що тіло людини складається з «будівельних блоків», співвідношення пропорцій яких завжди дорівнює нашому заповітному числу- Phi.

 

Золотий переріз - гармонійна пропорція

В математиці пропорцією (лат. proportio) називають рівність двох відносин:

a: b = c: d.

Відрізок прямої АВ можна розділити на дві частини наступними способами:

• на дві рівні частини - АВ: АС = АВ: ВС;

• на дві нерівні частини в будь-якому відношенні (такі частини пропорції не утворюють);

• таким чином, коли АВ: АС = АС: ВС.

Останнє і є золотий розподіл або поділ відрізка в крайньому і середньому відношенні. Золотий переріз - це таке пропорційне ділення відрізка на нерівні частини, при якому весь відрізок так відноситься до більшої частини, як сама велика частина відноситься до меншої; або іншими словами, менший відрізок так відноситься до більшого, як більший до всього a: b = b: c або  с:b = b: а.

Рис. 1. Геометричне зображення золотої пропорції.

 Практичне знайомство з золотим перерізом починають з поділу відрізка прямої в золотій пропорції за допомогою циркуля і лінійки.

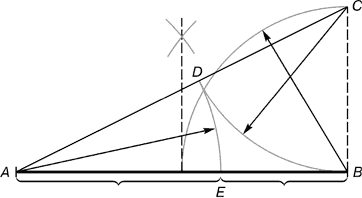
Рис. 2. Розподіл відрізка прямої по золотому перетину. BC = 1/2 AB; CD = BC

З точки В проводиться перпендикуляр, що дорівнює половині АВ. Отримана точка С з'єднується лінією з точкою А. На отриманій лінії відкладається відрізок ВС, що закінчується точкою D. Відрізок AD переноситься на пряму АВ. Отримана при цьому точка Е ділить відрізок АВ у співвідношенні золотої пропорції.

Відрізки золотої пропорції виражаються нескінченним ірраціональним дробом  

AE = 0,618 ..., якщо АВ прийняти за одиницю, ВЕ = 0,382 ... Для практичних цілей часто використовують наближені значення 0,62 і 0,38. Якщо відрізок АВ прийняти за 100 частин, то більша частина відрізка дорівнює 62, а менша - 38 частинам.

Властивості золотого перетину описуються рівнянням :

x² - x - 1 = 0.

Рішення цього рівняння:

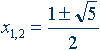
 Властивості золотого перерізу створили навколо цього числа романтичний ореол таємничості.

Другий золотий переріз

Болгарський журнал «Отечество» (№ 10, 1983 р.) опублікував статтю Цвєтана Цекова-Олівця «Про другий золотий переріз», який випливає з основного перетину і дає інше відношення 44: 56.

Така пропорція виявлена ​​в архітектурі, а також має місце при побудові композицій зображень подовженого горизонтального формату.

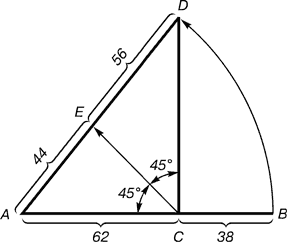
Рис. 3. Побудова другого золотого перерізу

 Розподіл здійснюється наступним чином. Відрізок АВ ділиться в пропорції золотого перерізу. З точки С проводиться перпендикуляр СD. Радіусом АВ знаходиться точка D, яка з'єднується лінією з точкою А. Прямий кут АСD ділиться навпіл. З точки С проводиться лінія до перетину з лінією AD. Точка Е ділить відрізок AD у відношенні 56: 44.

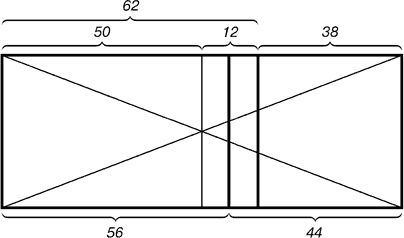
Рис. 4. Розподіл прямокутника лінією другого золотого перерізу

На малюнку показано положення лінії другого золотого перерізу. Вона знаходиться посередині між лінією золотого перерізу і середньою лінією прямокутника.

Золотий трикутник

Для знаходження відрізків золотої пропорції висхідного і низхідного рядів можна користуватися пентаграмою.

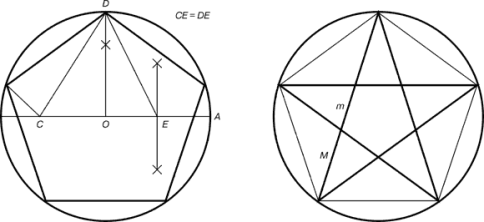
Рис. 5. Побудова правильного п'ятикутника і пентаграми

Для побудови пентаграми необхідно побудувати правильний п'ятикутник. Спосіб його побудови розробив німецький живописець і графік Альбрехт Дюрер (1471 ... 1528). 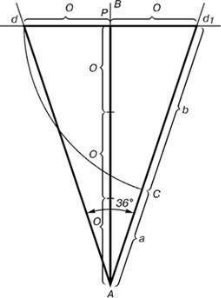Нехай O - центр кола, A - точка на колі та Е - середина відрізка ОА. Перпендикуляр до радіуса ОА, проведений  в точці О, перетинається з колом  в точці D. Користуючись циркулем, відкладемо на діаметрі відрізок CE = ED. Довжина сторони вписаного в коло правильного п'ятикутника дорівнює DC. Відкладаємо на колі  відрізки DC і отримаємо п'ять точок для накреслення правильного п'ятикутника. З'єднуємо кути п'ятикутника через один діагоналями і отримуємо пентаграму. Всі діагоналі п'ятикутника ділять один одного на відрізки, пов'язані між собою золотою пропорцією.

Кожен кінець п'ятикутної зірки являє собою золотий трикутник. Його сторони утворюють кут 36 ° при вершині, а пряма, відкладена на бічну сторону, ділить її в пропорції золотого перерізу. Проводимо пряму АВ. Від точки А відкладаємо на ній три рази відрізок О довільної величини, через отриману точку Р проводимо перпендикуляр до лінії АВ, на перпендикуляр вправо і вліво від точки Р відкладаємо відрізки О. Отримані точки d і d1 з'єднуємо прямими з точкою А. Відрізок dd1 відкладаємо на лінію Ad1, отримуючи точку С. Вона розділила лінію Ad1 в пропорції золотого перерізу. Лініями Ad1 і dd1 користуються для побудови «золотого» прямокутника.

Числа Фібоначчі

Леонардо Фібоначчі (1180-1240).

Великий італійський математик, автор «Книги абака».

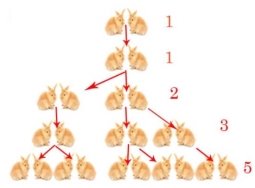Ця книга кілька століть залишалася основним сховищем відомостей по арифметиці і алгебрі. Саме за працями Л. Фібоначчі вся Європа освоювала арабські цифри, систему рахунку, а також практичну геометрію. Вона залишалася настільним підручником, мало не до епохи Декарта (а це вже 17 століття!), в якому були зібрані всі відомі на той час завдання. Одне із завдань - «Скільки пар кроликів в один рік від однієї пари народиться». Хтось помістив пару кроликів в якомусь місці, огородженому з  усіх боків стіною, щоб дізнатися, скільки пар кроликів народиться при цьому протягом року, якщо природа кроликів така, що через місяць пара кроликів народила на світ іншу пару, а народжують кролики з другого місяця після свого народження.

Розмірковуючи на цю тему, Фібоначчі вибудував такий ряд цифр:

Місяці	0	1	2	3	4	5	6	7	8	9	10	11	12	І.т.д.
Пари кроликів	0	1	1	2	3	5	8	13	21	34	55	89	144	І.т.д.

 

     Саме в цьому завданні з'являється послідовність, що обезсмертила ім'я Фібоначчі:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

   У цій послідовності сума будь-яких двох попередніх чисел дорівнює наступному числу: 1 +2 = 3, 3 +5 = 8, 5 +8 = 13, .... Відношення будь-якого числа послідовності до попереднього коливається навколо позначки, що ще в давнину мало назву золотого перетину : 1,61803398 ...

 «Золотий перетин» визначається як таке позитивне число, яке на одиницю більше зворотного до нього числа: t - = 1.

Кожне третє число Фібоначчі парне, кожне четверте ділиться на три, кожне п'ятнадцяте закінчується нулем. Число а_n ділиться на число а_k тоді і тільки тоді, коли n ділиться на k.

Числа Фібоначчі - послідовність цілих чисел {Fn}, задана за допомогою рекурентного співвідношення.

Послідовність чисел Фібоначчі починається так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 ...

Іноді Числа Фібоначчі розглядають для від’ємних n. Ряд, що відповідає визначенню чисел Фібоначчі

(F_n = F_{n - 1} + F_{n - 2}):

 ...,-55, 34, -21, 13, -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, ...

n	-10	-9	-8	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8	9	10
Fn	-55	34	-21	13	-8	5	-3	2	-1	1	0	1	1	2	3	5	8	13	21	34	55

 

Можна побачити, що F _{- n} = (- 1) ^{n + 1}F_n. Для чисел Фібоначчі з від’ємними індексами залишаються вірними більшість нижченаведених властивостей (але не всі!).

Отже, можна сказати, що тільки це відношення - 0,618: 0,382 - дає безперервний поділ відрізка прямої в золотій пропорції, збільшення його або зменшення до нескінченності, коли менший відрізок так відноситься до більшого, як більший до всього.

Фібоначчі також займався вирішенням практичних потреб торгівлі: за допомогою якої найменшої кількості тягарців можна зважити товар? Фібоначчі доводить, що оптимальною є така система тягарців: 1, 2, 4, 8, 16 ...

Узагальнений золотий переріз

Ряд Фібоначчі міг би залишитися тільки математичним казусом, якби не та обставина, що всі дослідники золотого поділу в рослинному і в тваринному світі, не кажучи вже про мистецтво, незмінно приходили до цього ряду як арифметичному вираженню закону золотого розподілу. Учені продовжували активно розвивати теорію чисел Фібоначчі і золотого перетину. Ю. Матіясевіч з використанням чисел Фібоначчі вирішує 10-ту проблему Гільберта. Виникають витончені методи рішення ряду кібернетичних задач (теорії пошуку, ігор, програмування) з використанням чисел Фібоначчі і золотого перетину. У США створюється навіть Математична Фібоначчі-асоціація, яка з 1963 року випускає спеціальний журнал. Одним з досягнень в цій області є відкриття узагальнених чисел Фібоначчі і узагальнених золотих перетинів.

Ряд Фібоначчі (1, 1, 2, 3, 5, 8) і відкритий ним же «двійковий» ряд тягарців 1, 2, 4, 8, 16 ... на перший погляд зовсім різні. Але алгоритми їх побудови досить схожі один на одного: у першому випадку кожне число є сума попереднього числа із самим собою 2 = 1 + 1; 4 = 2 + 2 ..., у другому - це сума двох попередніх чисел 2 = 1 + 1 , 3 = 2 + 1, 5 = 3 + 2 .... Чи не можна відшукати загальну математичну формулу, за допомогою якої можна отримати  і «двійковий» ряд, і ряд Фібоначчі? А може ця формула дасть нам нові числові множини, що володіють якимись новими унікальними властивостями?

Задамося числовим параметром S, який може приймати будь-які значення: 0, 1, 2, 3, 4, 5 ... Розглянемо числовий ряд S + 1, перші члени якого - одиниці, а кожні з наступних дорівнюють сумі двох членів попереднього і віддаленого від попереднього на S кроків. Якщо n-й член цього ряду ми позначимо через φS (n), то отримаємо загальну формулу φS (n) = φS (n - 1) + φS (n - S - 1).

Очевидно, що при S = ​​0 з цієї формули ми одержимо «двійковий» ряд, при S = ​​1 - ряд Фібоначчі, при S = ​​2, 3, 4. нові ряди чисел, які отримали назву S-чисел Фібоначчі.

У загальному вигляді золота S-пропорція є позитивний корінь рівняння золотого S-перетину x^{S +1} - x^S - 1 = 0.

Неважко показати, що при S = ​​0 виходить розподіл відрізка навпіл, а при S = ​​1-знайомий класичний золотий перетин. Відношення сусідніх S-чисел Фібоначчі з абсолютною математичною точністю збігаються із золотими S-пропорціями! Математики в таких випадках говорять, що золоті S-перерізи є числовими інваріантами S-чисел Фібоначчі.

Факти, що підтверджують існування золотих S-перерізів в природі, приводить білоруський вчений Е.М. Сороко в книзі «Структурна гармонія систем» (Мінськ, «Наука і техніка», 1984). Виявляється, наприклад, що добре вивчені подвійні сплави володіють особливими, яскраво вираженими функціональними властивостями (стійкі в термічному відношенні, тверді, зносостійкі, стійкі до окислювання і т. п) тільки в тому випадку, якщо питомі ваги вихідних компонентів пов'язані один з одним однією з золотих S-пропорцій. Це дозволило автору висунути гіпотезу про те, що золоті S-перерізи є числовими інваріантами систем, що самоорганізуються. Будучи підтвердженою експериментально, ця гіпотеза може мати фундаментальне значення для розвитку синергетики - нової галузі науки, що вивчає процеси в самоорганізованих системах.

За допомогою кодів золотої S-пропорції можна виразити будь-яке дійсне число у вигляді суми ступенів золотих S-пропорцій з цілими коефіцієнтами.

Принципова відмінність такого способу кодування чисел полягає в тому, що основами нових кодів, що представляють собою золоті S-пропорції, при S> 0 опиняються ірраціональними числами. Таким чином, нові системи числення з ірраціональними основами, так би мовити, ставлять «з голови на ноги» історично сформовану ієрархію відношень між числами раціональними та ірраціональними. Справа в тому, що спочатку були «відкриті» числа натуральні; потім їх відношення - числа раціональні. І лише пізніше з'явилися ірраціональні числа. Скажімо, в десятковій, п’ятеричній, двійковій та інших класичних позиційних системах числення як своєрідна першооснова були обрані натуральні числа - 10, 5, 2, - з яких вже за певними правилами конструювалися всі інші натуральні, а також раціональні та ірраціональні числа.

Свого роду альтернативою існуючим способам числення виступає нова, ірраціональна система, в якості першооснови і початку числення якої обрано ірраціональне число (яке є, нагадаємо, коренем рівняння золотого перетину); через нього вже виражаються інші дійсні числа.

У такій системі числення будь-яке натуральне число завжди можна представити у вигляді кінцевої - а не нескінченної, як думали раніше! - суми ступенів кожної з золотих S-пропорцій. Це одна з причин, чому «ірраціональна» арифметика, володіючи дивовижною математичною простотою і витонченістю, як би увібрала в себе кращі якості класичної двійкової та «Фібоначчієвої» арифметик.

Історія золотого перерізу

Прийнято вважати, що поняття про золотий переріз ввів у науковий обіг Піфагор, давньогрецький філософ і математик (VI ст. до н.е.). Є припущення, що Піфагор своє знання золотого поділу запозичив у єгиптян і вавілонян. І дійсно, пропорції піраміди Хеопса, храмів, барельєфів, предметів побуту і прикрас з гробниці Тутанхамона свідчать, що єгипетські майстри користувалися співвідношеннями золотого перерізу при їх створенні. Французький архітектор Ле Корбюзье винайшов, що в рельєфі з храму фараона Мережі I в Абідосі і в рельєфі, що зображує фараона Рамзеса, пропорції фігур відповідають величинам золотого перерізу. Зодчий Хесира, зображений на рельєфі дерев'яної дошки з гробниці його імені, тримає в руках вимірювальні інструменти, у яких зафіксовані пропорції золотого розподілу. Греки були майстерними геометрами. Навіть арифметиці навчали своїх дітей за допомогою геометричних фігур. Квадрат Піфагора і діагональ цього квадрата були підставою для побудови динамічних прямокутників.

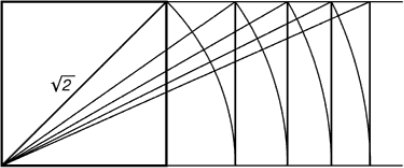
Рис. 7. динамічні прямокутники

Платон (427 ... 347 рр.. До н.е.) також знав про золотий перетин. Його діалог «Тімей» присвячений математичним і естетичним поглядам школи Піфагора і, зокрема, питанням золотого перетину. У фасаді давньогрецького храму  Парфенона присутні золоті пропорції. При його розкопках виявлені циркулі, якими користувалися архітектори і скульптори античного світу. У помпейських циркулях (музей в Неаполі) також закладені пропорції золотого розподілу.

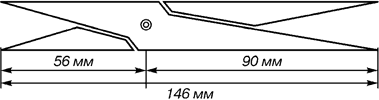
Рис. 8. Античний циркуль золотого перетину

У античній літературі, що дійшла до нас, золотий розподіл вперше згадується в  «Початку» Евкліда. У 2-ій книзі «Початок» дається геометрична побудова золотого поділу.  Після Евкліда дослідженням золотого перерізу займалися Гіпсікл (II ст. до н.е.), Папп (III ст. н.е.) і ін У середньовічній Європі з золотим перерізом познайомилися по арабських перекладах «Початку» Евкліда.  Перекладач Дж. Кампано з Наварри (III ст.) зробив до перекладу коментарі. Секрети золотого перерізу ревно оберігалися, зберігалися в суворій таємниці. Вони були відомі тільки обраним. В епоху Відродження посилюється інтерес до золотого перерізу серед учених і художників у зв'язку з його застосуванням як у геометрії, так і в мистецтві, особливо в архітектурі. Леонардо да Вінчі, художник і вчений, бачив, що у італійських художників емпіричний досвід великий, а знань мало . Він почав писати книгу по геометрії, але в цей час з'явилася книга ченця Луки Пачолі, і Леонардо залишив свою витівку. На думку сучасників та істориків науки, Лука Пачолі був справжнім світилом, найбільшим математиком Італії в період між Фібоначчі і Галілеєм. Лука Пачолі був учнем художника П'єро делла Франчески, що написав дві книги, одна з яких називалася «Про перспективу в живописі». Його вважають творцем нарисної геометрії. Лука Пачолі прекрасно розумів значення науки для мистецтва. У 1496 р на запрошення герцога Моро він приїжджає в Мілан, де читає лекції з математики. У Мілані при дворі Моро у той час працював і Леонардо да Вінчі. У 1509 р. у Венеції була видана книга Луки Пачолі «Божественна пропорція» з блискуче виконаними ілюстраціями, через що

вважають, що їх зробив Леонардо да Вінчі. Книга була захопленим гімном золотої пропорції. Серед багатьох достоїнств золотої пропорції чернець Лука Пачолі не забув назвати і її «божественну суть» як вираження божественної триєдності: бог син, бог батько і бог дух святого (малося на увазі, що малий відрізок є уособленням бога сина, більший відрізок - бога батька, а весь відрізок - бога духу святого).

Леонардо да Вінчі також багато уваги приділяв вивченню золотого перерізу. Він робив перетин стереометричного тіла, утвореного правильними п'ятикутниками, і кожного разу отримував прямокутники з відношенням сторін у золотому діленні. Тому він дав цьому поділу назву золотий перетин. Так воно і тримається досі як найпопулярніше.

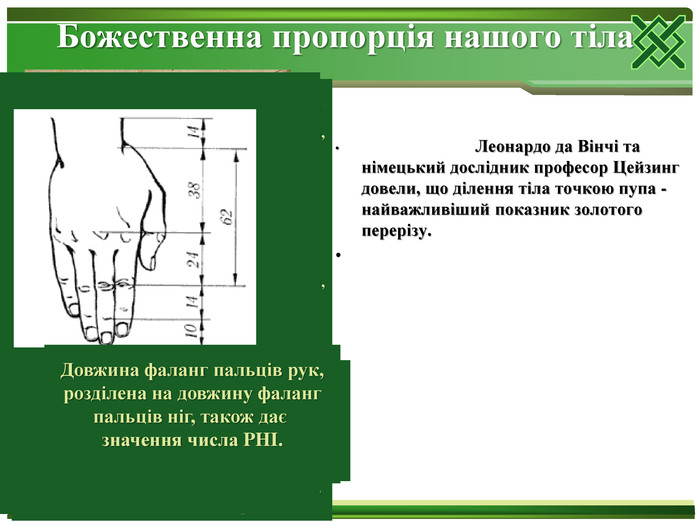
У той же час на півночі Європи, в Німеччині, над тими ж проблемами працював Альбрехт Дюрер. Він пише: «Необхідно, щоб той, хто щось вміє, навчив цього інших, які цього потребують. Це я і хотів учинити ».Судячи по одному з листів Дюрера, він зустрічався з Лукою Пачолі під час перебування в Італії. Альбрехт Дюрер докладно розробляє теорію пропорцій людського тіла. Тіло людини ділиться в золотих пропорціях лінією поясу, а також лінією, проведеною через кінчики середніх пальців опущених рук, нижня частина обличчя - ротом і т.д.

Великий астроном XVI в. Іоган Кеплер назвав золотий переріз одним зі скарбів геометрії. Він перший звертає увагу на значення золотої пропорції для ботаніки (зростання рослин та їх будова).

Кеплер називав золоту пропорцію такою, що продовжує саму себе. «Влаштована вона так, - писав він, - що два молодших члена цієї нескінченної пропорції в сумі дають третій член, а будь-які два останні члена, якщо їх скласти, дають наступний член, причому та ж пропорція зберігається до нескінченності ».

Побудова ряду відрізків золотої пропорції можна робити як у бік збільшення (зростаючий ряд), так і в бік зменшення (спадний ряд).

Якщо на прямий довільної довжини, відкласти відрізок m, поруч відкладаємо відрізок M. На підставі цих двох відрізків вибудовуємо шкалу відрізків золотої пропорції висхідного і низхідного рядів.

Рис. 9. Побудова шкали відрізків золотої пропорції

 У наступні століття правило золотої пропорції перетворилося в академічний канон. Знову «відкрито» золотий перетин було в середині XIX в. У 1855 р. німецький дослідник золотого перетину професор Цейзинг опублікував свою працю «Естетичні дослідження».

Він абсолютизував пропорцію золотого перерізу, оголосивши його універсальним 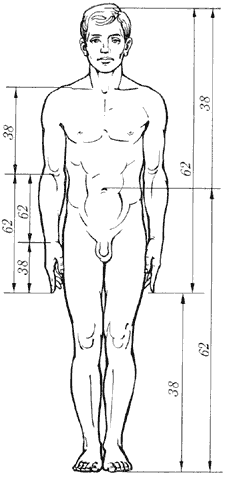 для всіх явищ природи і мистецтва. У Цейзинга були численні послідовники, але були й супротивники, які оголосили його вчення про пропорції «математичною естетикою».

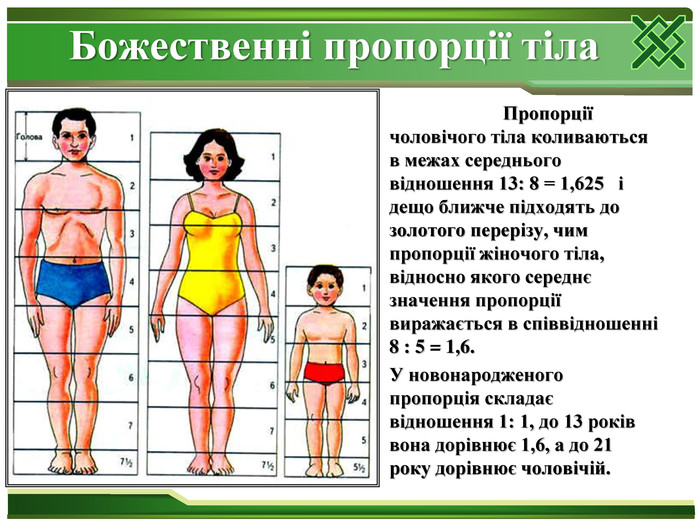
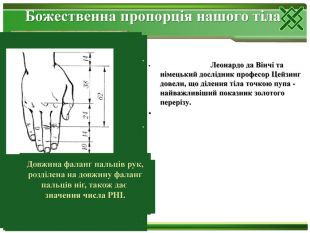
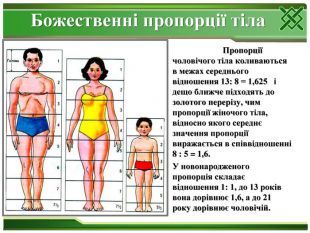
Цейзинг виконав колосальну роботу. Він виміряв близько двох тисяч людських тіл і прийшов до висновку, що золотий переріз виражає середній статистичний закон. Ділення тіла точкою пупа - найважливіший показник золотого перерізу. Пропорції чоловічого тіла коливаються в межах середнього відношення 13: 8 = 1,625  і трохи ближче підходять до золотого перерізу, ніж пропорції жіночого тіла, відносно якого середнє значення пропорції виражається в співвідношенні 8: 5 = 1,6. У новонародженого пропорція становить відношення 1: 1, до 13 років вона дорівнює 1,6, а до 21 року дорівнює чоловічій. Пропорції золотого перерізу проявляються і у відношенні інших частин тіла - довжина плеча, передпліччя і кисті, кисті і пальців і т.д.

Справедливість своєї теорії Цейзинг перевіряв на грецьких статуях. Найбільш докладно він розробив пропорції Аполлона Бельведерського. Були досліджені грецькі вази, архітектурні споруди різних епох, рослини, тварини, пташині яйця, музичні тони, віршовані розміри. Цейзинг дав визначення золотому перетину, показав, як воно виражається у відрізках прямої і в цифрах. Коли цифри, що виражають довжини відрізків, були отримані, Цейзинг побачив, що вони складають ряд Фібоначчі, який можна продовжувати до нескінченності в одну і в іншу сторону. Наступна його книга мала назву «Золотий перетин як основний морфологічний закон в природі і мистецтві». У 1876 р. в Росії була видана невелика книжка, майже брошура, з викладом цієї праці Цейзинга. Автор сховався під ініціалами Ю.Ф.В. У цьому виданні не згаданий жоден твір живопису.

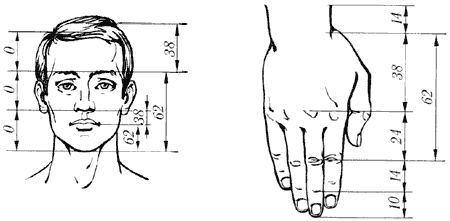
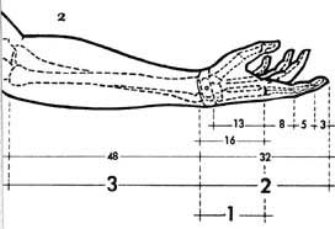
Рис. 10. Золоті пропорції в частинах тіла людини

В кінці XIX - початку XX ст. з'явилося чимало чисто формалістичних теорій про застосування золотого перетину у творах мистецтва і архітектури. З розвитком дизайну та технічної естетики чинність закону золотого перетину розповсюдилася на конструювання машин, меблів і т.д.

                                    

                                    

                                   

Теорема Піфагора і числа Фібоначчі

Принципи формоутворення в природі

Все, що набувало якусь форму, утворювалося, росло, прагнуло зайняти місце в просторі і зберегти себе. Це прагнення знаходить здійснення в основному в двох варіантах - ріст нагору або розстеляння по поверхні землі і закручування по спіралі.

Раковина закручена по спіралі. Якщо її розгорнути, то виходить довжина, що трохи поступається довжині змії. Невелика десятисантиметрова раковина має спіраль довжиною 35 см. Спіралі дуже поширені в природі.

.

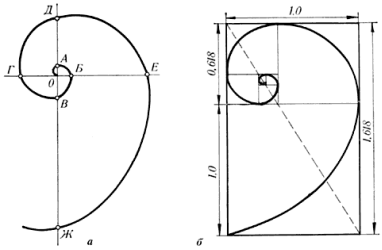
Рис. 12. Спіраль Архімеда

Форма спірально завитої раковини привернула увагу Архімеда. Він вивчав її і вивів рівняння спіралі. Спіраль, накреслена по цьому рівнянню, називається його іменем. Збільшення її кроку завжди рівномірно. В даний час спіраль Архімеда широко застосовується в техніці.

Ще Гете підкреслював тенденцію природи до спіральності. Гвинтоподібне і спіралеподібне розташування листя на гілках дерев помітили давно. Спіраль побачили в розташуванні насіння соняшнику, в шишках сосни, ананасах, кактусах і т.д. Спільна робота ботаніків і математиків пролила світло на ці дивовижні явища природи. З'ясувалося, що в розташуванні листя на гілці (філотаксіс), насіння соняшнику, шишок сосни проявляє себе ряд Фібоначчі, а отже, проявляє себе закон золотого перетину. Павук плете павутину спіралеподібно. Спіраллю закручується ураган. Перелякане стадо північних оленів розбігається по спіралі. Молекула ДНК закручена подвійною спіраллю. Гете називав спіраль "кривою життя».

Серед придорожніх трав росте нічим не примітна рослина - цикорій. Придивимося до нього уважно. Від основного стебла утворився відросток. Тут же розташувався перший листок.

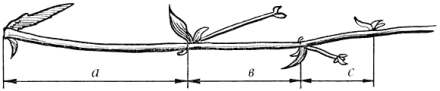
Рис. 13. Цикорій

Відросток робить сильний викид у простір, зупиняється, випускає листок, але вже коротше першого, знову робить викид в простір, але вже меншої сили, випускає листок ще меншого розміру і знову викид. Якщо перший викид прийняти за 100 одиниць, то другий рівний 62 одиницям, третій - 38, четвертий - 24 і т.д. Довжина пелюсток теж підпорядкована золотій пропорції.

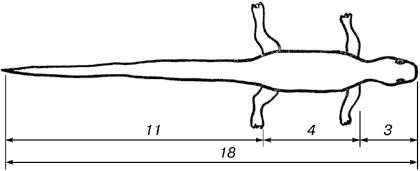
Рис. 14. Ящірка живородна

У ящірці з першого погляду уловлюються приємні для нашого ока пропорції - довжина її хвоста так відноситься до довжини решти тіла, як 62 до 38.

І в рослинному, і в тваринному світі наполегливо пробивається формотворна тенденція природи - симетрія щодо напрямку зростання і руху. Тут золотий перетин проявляється в пропорціях частин перпендикулярно до напрямку росту.

 

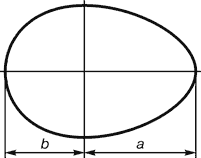
Рис. 15. Яйце птаха

Великий Гете, поет, природодослідник і художник (він малював і писав аквареллю), мріяв про створення єдиного вчення про форму, утворення і перетворення органічних тіл. Це він увів у науковий обіг термін морфологія.

П'єр Кюрі на початку нашого століття сформулював ряд глибоких ідей симетрії. Він стверджував, що не можна розглядати симетрію якого-небудь тіла, не враховуючи симетрію навколишнього середовища.

Закономірності «золотої» симетрії виявляються в енергетичних переходах елементарних частинок, в будові деяких хімічних сполук, в планетарних і космічних системах, в генних структурах живих організмів. Ці закономірності, як вказано вище, є в будові окремих органів людини і тіла в цілому, а також проявляються в біоритмах і функціонуванні головного мозку і зорового сприйняття.

Бивні слонів і вимерлих мамонтів, кігті левів і дзьоби папуг являють собою логарифмічні форми і нагадують форму осі, схильної звернутися в спіраль.

.У живій природі широко поширені форми, засновані на "пентагональнальній" симетрії (морські зірки, морські їжаки,

 

квіти латаття, шипшини, глоду, гвоздики, груші, черемхи, яблуні, суниці та багатьох інших). Праворуч показана квітка китайської троянди з яскраво вираженою "пентагональною" симетрією. Також можна зустріти золоту пропорцію у розрізі яблука (пентаграма).

Молекула ДНК складається з двох вертикально переплетених між собою спіралей. Довжина кожної з цих спіралей становить 34 ангстрема, ширина 21 ангстрема. (1 ангстрем - одна стомільйонний частка сантиметра).

Так ось 21 і 34 - це цифри, наступні один за одним у послідовності чисел Фібоначчі, тобто співвідношення довжини і ширини логарифмічної спіралі молекули ДНК несе в собі формулу золотого перетину 1:1,618.

Дуже досконала форма бабки, яка створена за законами золотої пропорції: відношення довжин хвоста і корпусу дорівнює відношенню загальної довжини до довжини хвоста. Багато комах (наприклад, метелики) в горизонтальному розрізі мають прості асиметричні форми, засновані на золотому перетині.

Золотий переріз присутній в будові всіх кристалів, але більшість кристалів мікроскопічно малі, тому ми не можемо розгледіти їх неозброєним оком. Однак сніжинки також представляють собою водні кристали, цілком доступні нашому погляду. Всі вишуканої краси фігури, які утворюють сніжинки, всі осі, кола та геометричні фігури в сніжинках також завжди без винятків побудовані за досконалою чіткою формулою золотого перетину.

Виявляється, що розташування листя на стеблах також носить строгий математичний характер і це явище називається в ботаніці "філлотаксісом".

 

 

 

У явищі філлотаксіса використовуються більш складні поняття симетрії, зокрема поняття "гвинтова вісь симетрії". Розглянемо, наприклад, розташування листя на стеблі рослини (ліворуч). Ми бачимо, що листя знаходяться на різних висотах стебла вздовж гвинтової лінії. Для того щоб перейти від нижнього листа до наступного, доводиться подумки повернути лист на деякий кут навколо вертикальної осі стебла, а потім підняти його на певний відрізок вгору. В цьому і полягає суть "гвинтовий симетрії»

А тепер розглянемо характерні "гвинтові осі", які виникають на стеблах рослин (Рис зліва). На Малюнку зображено стебло рослини з гвинтовою віссю симетрії третього порядку. Простежимо лінію розміщення листочків на цьому малюнку. Для того, щоб перейти від листа 1 до листа 2, слід повернути перший навколо осі стебла на 120 ° проти годинникової стрілки (якщо дивитися знизу) і потім пересунути листок 1 уздовж стебла по вертикалі до тих пір, поки він не стане сумісний з листком 2. Повторюючи подібну операцію, перейдемо від листа 2 до листа 3, а потім до листа 4. Звернемо увагу на те, що листок 4 лежить над листком 1 (як би повторює його, але вище) і що, йдучи від листа 1 до листа 4, ми тричі здійснили поворот на кут 120 °, тобто здійснили повний оберт навколо осі стебла (120 ° х 3 = 360 °).

Кут повороту гвинтової осі у ботаніків називається "кутом розбіжності листя". Вертикальна пряма, що з'єднує два листка, розташовані один над одним на стеблі, називається "ортостихою". Відрізок 1-4 ортостихи відповідає повній трансляції гвинтової осі. Число обертів навколо осі стебла для переходу від нижнього листа до розміщених вище, розташованому в точності над нижнім, може бути рівним не тільки одиниці, але і двом, трьом і т.д. Це число оборотів називається "листовим циклом". У ботаніці прийнято характеризувати гвинтове листорозміщення за допомогою дробу, чисельником якого є число оборотів в листовому циклі, а знаменником - число листя в цьому циклі. У розглянутому нами випадку ми маємо гвинтову вісь типу 1/3.

Зауважимо, що існують і більш хитромудрі осі, наприклад, типу 3/8, 5/13 і т.д.

Якими можуть бути числа a і b, що характеризують гвинтову вісь типу a / b

Дріб 1/2 властива злакам, березі, винограду; 1/3 - осоці, тюльпану, вільсі; 2/5 - груші, смородині, сливі; 3/8 - капусті, редисці, льону; 5/13 - ялині, жасмину і т . д.

Ботаніки стверджують, що дроби, які характеризують гвинтові осі рослин, утворюють строгу математичну послідовність, що складається з відношень сусідніх чисел Фібоначчі, тобто:

1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34, ...

Згадаймо, що ряд Фібоначчі є наступна послідовність чисел:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

Яка ж "фізична" причина, що лежить в основі "законів філлотаксіса"?

Відповідь дуже проста. Виявляється, що саме при такому розташуванні листя досягається максимум припливу сонячної енергії до рослини.

Практично всі суцвіття і щільно упаковані ботанічні структури (соснові і кедрові шишки, ананаси, кактуси, головки соняхів і багато інших) також строго слідують числам Фібоначчі (Насіння в головці соняшника розташовуються по спіралях, при цьому відношення числа лівих і правих спіралей дорівнює відношенню сусідніх чисел Фібоначчі).

У біологічному і рослинному світі вступає в дію принцип економії матерії, який не діє у неорганічному світі.

Яскравим прикладом цього є прагнення живих організмів до економії кісткової субстанції при розподілі матерії, що дає максимум міцності у всіх потрібних напрямках.

Крім цього, живі організми проявляють лише один властивий їм феномен - феномен зростання. Неорганічні кристали збільшуються шляхом приєднання ідентичних елементів; живий організм росте шляхом "всмоктування", що йде зсередини і прямує назовні.

Відповідаючи на запитання: "Де межа між живою і мертвою природою?" багато відомих фахівці в області симетрії і кристалографії звертають увагу на те, що ця відмінність полягає у використанні в живих організмах так званої "пентагональної" симетрії, пов'язаної з золотим перетином.

Кількість пелюсток у квітці відповідає ряду Фібоначчі 1; 2; 3; 5; 8; 13; 21…

Біла кала 1 пелюстка

Молочай 2 пелюстки

Трилліум 3 пелюстки

Глоксія 5 пелюсток

Вовчий слід 8 пелюсток

Чорноока Сазан 13 пелюсток

Хризантема 21 пелюстка

 

Золотий кут (137,5 ° ...)

Золотий кут (137,5 ° ...) -Послідовність Фібоначчі обмежена повним оборотом в 360°. Такий кут дозволяє досягти ідеального розташування зачатків (Якщо кожен новий зачаток буде з'являтися під цим кутом по відношенню до попереднього, ймовірність того, що два зачатка будуть розвиватися в одному і тому ж напрямку, повністю виключається. Це означає, що зачатки будуть розташовуються по спіралі , а не радіально). У природі існує безліч подібних феноменів.

 Золотий перетин застосовували також астрономи, які описували закономірності планет сонячної системи.

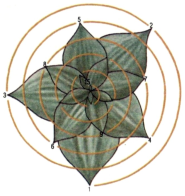Числа Фібоначчі з'являються також у питаннях, пов'язаних з дослідженням шляхів в різних геометричних конфігураціях.

 

 

 

 

 

 

Золотий переріз в живопису

Ще в епоху Відродження художники відкрили, що будь-яка картина має певні точки, якими мимоволі приковує нашу увагу, так звані зорові центри. При цьому абсолютно неважливо, який формат має картина - горизонтальний або вертикальний. Таких точок всього чотири, вони ділять величину зображення по горизонталі і вертикалі в золотому перетині, тобто розташовані вони на відстані приблизно 3/8 і 5/8 від відповідних країв площини.

 

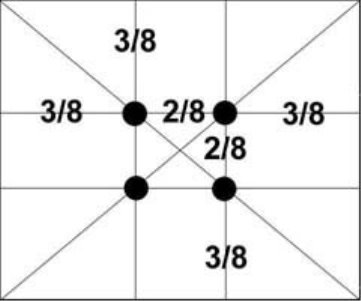
Дане відкриття у художників того часу отримало назву "золотий перетин" картини. Тому, для того щоб привернути увагу до головного елемента фотографії, необхідно поєднати цей елемент з одним із зорових центрів.

 

 

 

 

 

 

 

картина М.М. Ге «Олександр Сергійович Пушкін в селі Михайлівському».  

На цій картині постать Пушкіна поставлена художником  зліва на лінії золотого перетину. Композиційна побудова картини подібна до картини Рєпіна. Голова військового знаходиться на іншій вертикальній лінії золотого перетину.

Широко використав золотий перетин у своїй творчості талановитий російський художник Костянтин Васильєв,але він рано пішов з життя. Ще будучи студентом Казанського художнього училища, він вперше почув про "золотий перетин". І з тих пір, приступаючи до кожної своєї роботи, він завжди починав з того, що подумки намагався визначити на полотні ті основні точки, куди повинні були притягуватися, як до невидимого магніту, всі сюжетні лінії картини. Яскравим прикладом картини, побудованої по принципу "золотого перетину", є картина "Біля вікна".

 

Про що хотів розповісти нам художник на цій картині? Про це можна лише здогадуватися. Одне безперечно - перед нами життя як воно є. Те, що двоє цих молодих людей нескінченно люблять один одного, ми розуміємо при першому погляді на картину. Але якщо він весь у владі свого нестримного пориву, готовий відстоювати свою любов перед ким завгодно, то її почуття щось стримує. Що саме - страх, гординя, вірність родовим традиціям? А може бути, інтуїція, природне чуття, більш властиве жіночому серцю, підказує їй, що не час їм зараз думати про кохання?

Наведемо приклад такого «подвійного золотого перетину» з живопису.

Приклад цей особливо цікавий тому, що він узятий з твору найвідомішого представника реалістичного напряму в живописі.

І той факт, що це зустрічається саме у нього, може служити докором тим забобонам, згідно з якими для реалізму нібито достатньо однієї побутової правди, строгість же композиційного листа аж ніяк не важлива і навіть мало не шкідлива!

Аналіз робіт справді великих майстрів реалізму говорить про інше. Проблеми композиції творчо мучили їх так само невпинно, як проблеми втілення правди життя, бо до кінця щиро відчута і до кінця повно виражена у своїх почуттях правда втілиться через всі засоби, які знаходяться в руках автора. Але про це вже було сказано детально і докладно. Перейдемо до прикладу.

Картина ця - «Бояриня Морозова». Автор - В. І. Суриков.

Та картина і той художник, про правдивість яких писав Стасов (у 1887 р.):

«... Суриков створив тепер таку картину, яка, по-моєму, є першою з усіх наших картин на сюжети з російської історії ... Сила правди, сила історичності, якими дихає нова картина Сурикова, вражаючі ... ».

Суриков писав про своє перебування в Академії:«... Найбільше композицією займався. Там мене «композитором» звали: я все природність і красу композиції вивчав. Удома сам собі завдання ставив і дозволяв ... ». Таким «композитором» Суриков залишався на все життя. Будь-яка його картина - живе тому підтвердження.

І найбільш яскраве - «Бояриня Морозова».

Тут поєднання «природності» і краси в композиції представлено, мабуть, найбільш багато.

Але що таке це поєднання «природності та краси», як не «органічність» в тому сенсі, як ми про неї говорили вище?

Але де йдеться про органічність, там ... шукай золотий перетин в пропорціях!

Той же Стасов писав про «Бояриню Морозову» як про «солістку» в оточенні «хору». Центральна «партія» належить самій боярині. Ролі її відведена середня частина картини. Вона окована точкою вищого зльоту і точкою нижчого спадання сюжету картини. Це - зліт руки Морозової з двуперстним хресним знаменням як вища точка. І це - безпорадно простягнута до тієї ж боярині рука, але на цей раз - рука старої - злиденної Мандрівниці, рука з останньою надією на порятунок.

Це дві центральні драматичні точки «ролі» боярині Морозової: «нульова» точка і точка максимального злету.

Єдність драми як би підкреслена тією обставиною, що обидві ці точки прикуті до вирішальної центральної діагоналі, що визначає весь основний лад картини.

Вони не збігаються буквально з цією діагоналлю, і саме в цьому - відмінність живої картини від мертвої геометричної схеми.

Але спрямованість до цієї діагоналі і зв’язок з нею наявні.

Постараємося просторово визначити, які ще вирішальні розтини проходять поблизу цих двох точок драми.

Маленька креслярсько-геометрична робота покаже нам, що обидві ці точки драми включають між собою два вертикальних перетини, які проходять на 0,618 ... від кожного краю прямокутника картини!

«Нижча точка» цілком збігається з перетином АВ, віддаленому на 0,618 ... від лівого краю.

А як справа з «вищою точкою»? На перший погляд маємо суперечність: адже перетин А₁В₁, віддалений на 0,618 ... від правого краю картини, проходить не через руку, і навіть не через голову або очі боярині, а виявляється десь перед ротом боярині! Тобто, іншими словами, - це вирішальний перетин, засіб максимально прикувати увагу, який ніби проходить по повітрю.

Згоден, що перед ротом.

Згоден, що по повітрю.

Але ніяк не згоден, що «даремно».

Навпаки!

Золотий перетин ріже тут дійсно по самому головному. І несподіванка тут тільки в тому, що саме це найголовніше - пластично не зображено.

Золотий перетин А₁В₁ проходить по слову, яке летить з уст боярині Морозової.

Бо не рука, не палаючі очі, не рот - тут головне. А вогненне слово фанатичного переконання.

У ньому, і саме в ньому, - найбільша сила Морозової.

Той же Стасов пише про неї, що вона «та сама жінка, про яку Авакум, глава тодішніх фанатиків, говорив в ті дні, що вона« лев серед овець »...».

Однак рука - зображена. Око - зображене. Особа - відображена. Голос - немає.

Що ж робить Суриков? В те місце, звідки виривався би «пластично не зображений» голос, він не поміщає ніякої деталі, здатної залучити до цього місця увагу глядача. Але він змушує цю увагу глядача бути ще сильнішою і ще схвильованіше затримуватися на цьому місці, бо це місце є пластично не зображеною точкою перетину двох вирішальних композиційних членувань, а саме - основної композиційної лінії діагоналі і лінії, яка проходить через золотий перетин. Тут Суриков засобами композиційних розчленовувань виходить за рамки вузько образотворчого пластичного викладу, і робить він це для того, щоб дати відчути те, що ціною одного пластичного зображення  неможливо було б показати! Він приковує увагу не тільки до боярині Морозової, не тільки до її обличчя, але як би і до самих слів полум'яного заклику, що виривається з її вуст.

Як бачимо, вища точка, так само як і нижча, дійсно і тут, як і у випадку «Потьомкіна», в рівній мірі виявляються на осях золотого перетину. Цікаво відзначити, що схожість йде ще глибше.

На картині І.І. Шишкіна "Корабельная роща" проглядаються мотиви золотого перетину. Яскраво освітлена сонцем сосна (що стоїть на першому плані) ділить довжину картини приблизно в золотому перетині. Праворуч від сосни - освітлений сонцем пагорок. Він ділить в золотому перетині праву частину картини по горизонталі. Зліва від головної сосни знаходиться безліч сосен - при бажанні можна з успіхом продовжити поділ картини в пропорціях золотого перетину.

Наявність в картині яскравих вертикалей і горизонталей, що поділяють її відносно золотого перетину, надає їй характер врівноваженості та спокою, відповідно до задуму художника. Коли художник створює картину з дією, яка бурхливо розвивається, подібна геометрична схема композиції (з переважанням вертикалей і горизонталей) стає неприйнятною.

Відчуття динаміки, хвилювання проявляється, мабуть, більш за все у інший простій геометричній фігури - спіралі. Багатофігурна композиція, виконана в 1509 - 1510 роках Рафаелем, коли прославлений живописець створював свої фрески у Ватикані, відрізняється динамізмом і драматизмом сюжету. Рафаель так і не довів свій задум до кінця, однак, його ескіз був гравійований невідомим італійським графіком Маркантініо Раймонді, який на основі цього ескізу і створив гравюру "Побиття немовлят".

Якщо на підготовчому ескізі Рафаеля подумки провести лінії, що йдуть від смислового центру композиції - точки, де пальці воїна зімкнулися навколо щиколотки дитини, - уздовж фігури дитини, жінки, що притискує її до себе, воїна з занесеним мечем і потім уздовж фігур такої ж групи в правій частині ескізу (на малюнку ці лінії проведені червоним кольором), а після цього з'єднати ці шматки кривої пунктиром, то з дуже великою точністю виходить золота спіраль. Це можна перевірити, вимірюючи відношення довжин відрізків, які висікаються спіраллю на прямих, що проходять через початок кривої.

Невідомо, чи насправді малював Рафаель золоту спіраль при створенні композиції "Побиття немовлят" або тільки "відчував" її. Проте з упевненістю можна сказати, що гравер Раймонді цю спіраль побачив. Про це свідчать додані їм нові елементи композиції, що підкреслюють розворот спіралі в тих місцях, де вона у нас позначена лише пунктиром. Ці елементи можна побачити на гравюрі Раймонді: арка моста, що йде від голови жінки, - у лівій частині композиції і лежаче тіло дитини - в її центрі.

Переходячи до прикладів "золотого перетину" в живописі, не можна не зупинити своєї уваги на творчості Леонардо да Вінчі. Подивимося уважно на картину "Джоконда".

                   

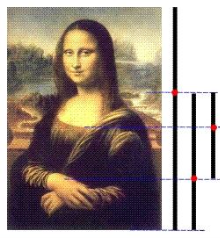
Портрет Мони Лізи (Джоконда) приваблює тим, що композиція малюнка побудована на "золотих трикутниках", точніше на трикутниках, які є шматками правильного зірчастого п'ятикутника. Зіниця лівого ока, через яку проходить вертикальна вісь полотна, знаходиться на перетині двох бісектрис верхнього золотого трикутника, які з одного боку, ділять навпіл кути при основі золотого трикутника, а з іншого боку, в точках перетину зі сторонами золотого трикутника ділять їх в пропорції Золотого перетин.

 Таким чином, Леонардо Да Вінчі використовував у своїй картині не тільки принцип симетрії, але і Золотий перетин.

За свідченням Аммореті можна припустити, що картина "Таємна Вечеря" була закінчена в 1497 році. На жаль, Леонардо да Вінчі виконав її фарбами, з яких деякі виявилися дуже неміцними. Вже через п'ятдесят років після закінчення, картина, за свідченням Вазарі, перебувала у дуже жалюгідному стані. Однак, якщо б у той час можна було виконати бажання короля Франциска I, виражене через шістнадцять років після закінчення картини, і, виламавши стіну, перевзти картину до Франції, то, можливо, вона збереглась би. Але цього не можна було зробити. У 1500 р. вода, що залила трапезу, остаточно зіпсувала стіну. Картина була кілька разів невдало реставрована у 1796 р., а після переходу французів через Альпи, Наполеон віддав строге розпорядження пощадити трапезу, але генерали, що слідували за ним, не звертаючи уваги на його наказ, перетворили це місце в стайню, а згодом в місце для сіна .

"Таємна вечеря" - найзріліший закінчений твір Леонардо. У цьому розписі майстер уникає всього того, що могло би затемнити основний хід зображених ним дій, він домагається рідкісної переконливості композиційного рішення. У центрі він розміщує фігуру Христа, виділяючи її просвітом двері. Апостолів він свідомо відсуває від Христа, щоб ще більше акцентувати його місце в композиції. Нарешті, з цією ж метою він змушує сходитися всі перспективні лінії в точці, безпосередньо розташованою над головою Христа. Учнів Леонардо розбиває на чотири симетричні групи, повні життя і руху. Стіл він робить невеликим, а трапезу – суворою і простою. Це дає йому можливість зосередити увагу глядача на фігурах, що володіють величезною пластичної силою. У всіх цих прийомах визначається глибока цілеспрямованість творчого задуму, в якій все зважено і враховано ... "

Картина «Святе сімейство» Мікеланджело визнана одним із шедеврів західноєвропейського мистецтва епохи Відродження.

     

Полотно, на якому написана «Таємна вечеря» Сальвадора Далі, має форму золотого прямокутника, сторони якого знаходяться в золотому відношенні.

 

Краса пропорційності

Сучасний модельний бізнес також використовує ідеальні пропорції, адже "все нове - це добре забуте старе":

Згідно до недавньої статті журналу Discover, краса дійсно може бути пропорційною, як стародавні греки припустили в своїй теорії золотого перетину, яка була заснована на математиці Піфагора. Доктор Марквардт, пластичний хірург, який працює з пацієнтами, що мають серйозні деформації або пошкодження, шукав систему пропорцій, які могли б допомогти йому з такими основними реконструкціями як підборіддя, ніс і навіть рот. Виконавши дослідження він виявив, що дійсно прекрасне обличчя повинно мати однакові пропорційні співвідношення, як золота середина. Доктор Марквардт створив за допомогою комп'ютера Золоту маску, яка дає тривимірне зображення ідеально пропорційного обличчя.

 

 

 

 

 

Золотий переріз в архітектурі

Одним з найкрасивіших творів давньогрецької архітектури є Парфенон (V ст. до н.е.)

 

На малюнках видно цілий ряд закономірностей, пов'язаних із золотим перерізом. Пропорції будівлі можна виразити через різні міри числа Ф=0,618...

Золоте співвідношення ми можемо побачити і у будівлі собору Паризької Богоматері(Нотр-пані де Пари), і в піраміді Хеопса.

     

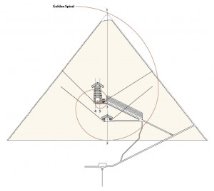
Пропорції піраміди Хеопса, храмів, барельєфів, предметів побуту і прикрас з гробниці Тутанхамона свідчать, що єгипетські майстри користувалися співвідношеннями золотого ділення при їх створенні. Французький архітектор Ле Корбюзье побачив, що в рельєфі з храму фараона і в рельєфі, що зображує фараона Рамзеса, пропорції фігур відповідають величинам золотого ділення. Архітектор Хесира, зображений на рельєфі дерев'яної дошки з гробниці його імені, тримає в руках вимірювальні інструменти, в яких зафіксовані пропорції золотого поділу.

Що стосується пірамід, то не тільки єгипетські піраміди побудовані у відповідності з ідеальними пропорціями золотого перетину, те ж саме явище виявлено і у Мексикансих пірамід.

 

Мексиканські піраміди

На поперечному перерізі піраміди видно форма, що подібна сходинкам. В першому ярусі 16 ступенів, у другому 42 ступені і в третьому - 68 ступенів.

Ці числа засновані на співвідношенні Фібоначчі наступним чином:

16 x 1.618 = 26

16 + 26 = 42

26 x 1.618 = 42

42 + 26 = 68

 

Пропорції Покровського собору на Червоній площі в Москві (більш відомого як храм Василя Блаженного) визначаються вісьмома членами ряду золотого перетину: 1, a, a₂ ... a₇. Багато членів цього ряду повторюються у елементах храму багаторазово, причому a + a₂ = 1, a₂ + a₃ = a, a₃ + a₄ = a₂, a₄ + a₅ = a₃ і т. д.

Мої дослідження

Мене зацікавила тема чисел Фібоначчі, і я вирішив евристичним шляхом перевірити, чи дійсно справджується теорія золотого перерізу.

Я виконав наступні виміри :

1. Перше моє дослідженням було таким,  що я попросив своїх однокласників сісти на лавку, і отримав виміри, які наближуються до золотого перетину.

 

 

№ з/п	Відрізок «а» (см)	Відрізок «b» (см)	Відношення
	115	137	0,839416058
	119	132	0,901515152
	91	160	0,56875
	123	128	0,9609375
	120	131	0,916030534
	124	127	0,976377953
	114	137	0,832116788
	123	128	0,9609375
	121	129	0,937984496
	108	144	0,75

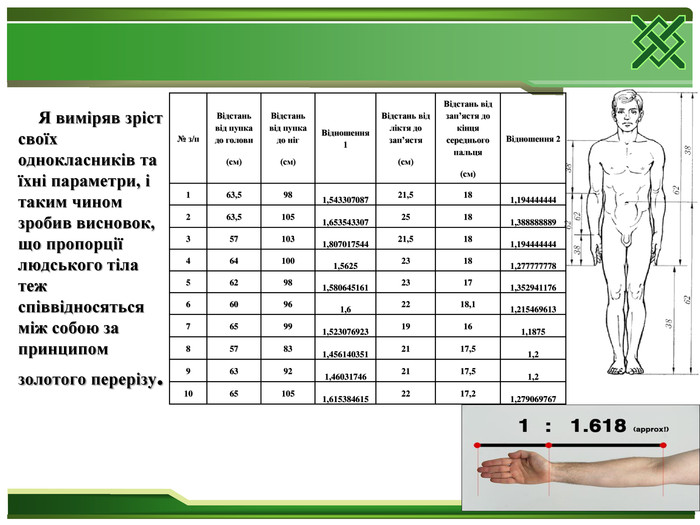
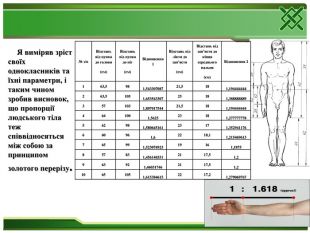
2. 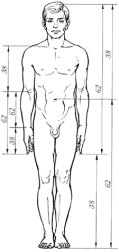     Я виміряв зріст своїх однокласників та їхні параметри, і таким чином зробив висновок, що пропорції людського тіла теж співвідносяться між собою за принципом золотого перетину.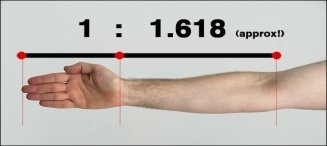

№ з/п	Відстань від пупка до голови (см)	Відстань від пупка до ніг (см)	Відношення 1	Відстань від ліктя до зап’ястя (см)	Відстань від зап’ястя до кінця середнього пальця (см)	Відношення 2
1	63,5	98	1,543307087	21,5	18	1,194444444
2	63,5	105	1,653543307	25	18	1,388888889
3	57	103	1,807017544	21,5	18	1,194444444
4	64	100	1,5625	23	18	1,277777778
5	62	98	1,580645161	23	17	1,352941176
6	60	96	1,6	22	18,1	1,215469613
7	65	99	1,523076923	19	16	1,1875
8	57	83	1,456140351	21	17,5	1,2
9	63	92	1,46031746	21	17,5	1,2
10	65	105	1,615384615	22	17,2	1,279069767

 

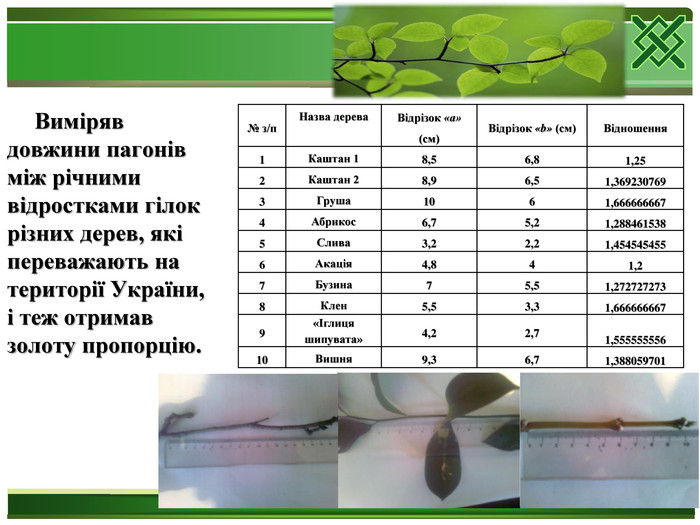
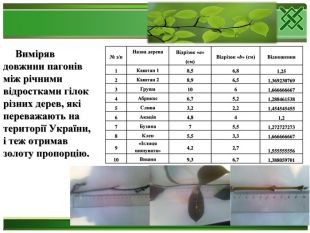
3. Виміряв  довжини пагонів між річними відростками гілок різних дерев, які переважають на території України, і теж отримав золоту пропорцію.

№ з/п	Назва дерева	Відрізок «а» (см)	Відрізок «b» (см)	Відношення
	Каштан 1	8,5	6,8	1,25
	Каштан 2	8,9	6,5	1,369230769
	Груша	10	6	1,666666667
	Абрикос	6,7	5,2	1,288461538
	Слива	3,2	2,2	1,454545455
	Акація	4,8	4	1,2
	Бузина	7	5,5	1,272727273
	Клен	5,5	3,3	1,666666667
	«Іглиця шипувата»	4,2	2,7	1,555555556
	Вишня	9,3	6,7	1,388059701

Висновок

Числа Фібоначчі якимось дивним чином пов'язані з будовою людини, з будовою його органів, серцевою діяльністю, і т.д.

Адже дивно, що числа, отримані в результаті задачі про кроликів, опинилися в такому взаємозв'язку? Можна припустити, що незабаром, в результаті досліджень учених, числа Фібоначчі будуть не захоплюючою математичною задачкою, а ляжуть в основу концепції знань про будову живої природи і наукового світорозуміння. Тим паче якщо врахувати, що інтерес до чисел Фібоначчі значно зріс: числа Фібоначчі вивчають на факультативних заняттях у школах, вивченням цих чисел захоплюються наукові студентські колективи.

Розглянуті нами факти отримані на основі статистичних даних, і поки що не піддаються осмисленню з боку прикладних наук про організацію життєдіяльності людини. Ці дані поки що не прозорі, але наукова думка не стоїть на місці, і тому слід очікувати появи нових закономірностей, пов'язаних з вивченням чисел Фібоначчі, які, як ми сподіваємося, істотно вплинуть на хід розвитку науки у вивченні живої природи. Можливо, і ми дуже цього чекаємо, золота пропорція зіграє вирішальну роль у вивченні механізму хвороб, які не піддаються  лікуванню на даному етапі розвитку нашої цивілізації.

 

Джерела інформації

 

1. В.И. Коробко "Золотая пропорция и проблемы гармонии систем" (1998 г.)
2. Виктор Лаврус статья "Золотое сечение"
3. Дюрер А. Дневники, письма, трактаты – Л., М., 1957.
4. Кеплер И. О шестиугольных снежинках. – М., 1982.
5. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
6. Сергей Эйзенштейн, Сергей Эйзенштейн о «золотом сечении» // «Академия Тринитаризма», М., Эл № 77-6567, публ.13357, 29.05.2006
7. Стахов А. "Код да Винчи и ряды Фибоначи" -И. Питер 2006
8. Стахов А. Коды золотой пропорции.
9. Цеков-Карандаш Ц. О втором золотом сечении. – София, 1983.
10. http://www.abc-people.com/data/leonardov/zolot_sech-txt.htm
11. http://world.lib.ru/s/shakirow_d_s/zolotoececxenie.shtml
12.  http://www.liveinternet.ru/community/1726655/post64489082/
13.  http://www.tech-to-life.com/publ/1-1-0-18
14. http://piramidlandia.at.ua/
15.  http://www.abc-people.com/idea/zolotsech/golden-section-pic002.htm
16.  http://www.tech-to-life.com/publ/
17. http://www.goldenmuseum.com/index_rus.html