ТЕМА: Числові функції. Область визначення і множина значень функції. Способи задання функції.

Тривалість 90 хв.

МЕТА:

Навчальна:

домогтися усвідомлення студентами змісту понять «функція», «функціональна залежність», «область визначення функції», «область значень функції», способи задання функції; здійснити первинне закріплення змісту вивчених понять; розпочати роботу з вироблення вмінь: а) задавати функціональні залежності формулами; б) працювати із функціями, заданими таблицею; в) обчислювати за формулою значення функції, якщо відомо значення аргументу, та розв'язувати обернену задачу.

Розвиваюча:

розвивати навички самоконтролю, логічне мислення, математичну мову, інтуїцію, вміння самостійно працювати та працювати в групах.

Виховна:

виховувати в студентів самостійність, кмітливість, старанність, наполегливість, творчу й пізнавальну самостійність.

Обладнання:

1. Набір слайдів для повторення і вивчення нового матеріалу.

2. Мультимедійний проектор.

3. Індивідуальні карточки-завдання.

 

Тип заняття: формування нових знань

Епіграф заняття: …              Природа формулює свої закони                      мовою математики.

Галілео Галілей

Структура:

№	Назва етапу	Тривалість
1.	Організаційний момент	2 хв.
2.	Актуалізація опорних знань.	9 хв
3.	Перевірка домашнього завдання	10 хв
4.	Вивчення нового матеріалу	25 хв
5.	Закріплення нового матеріалу	23 хв
6.	Самостійна робота	12 хв
7.	Домашнє завдання	2 хв
8.	Підведення підсумків	7 хв

Хід заняття

І. Організаційний момент (перевірка присутності студентів, наявність форми одягу)

 ІІ. Актуалізація опорних знань

ІІІ. Перевірка домашнього завдання

• Фронтальне опитування

1. Що називається вiдсотком?

2. Подайте у виглядi дробу (звичайного i десяткового):

2 %; 20 %; 50 %; 63,5 %; 75 %; 100 %; 137 %; 250 %.

3. Подайте у виглядi вiдсоткiв:

0,3; 0,04; 0,23; 1 2 ; 1,05;1 3 4 ; 2,45.

4. Що називається пропорцiєю? Наведiть приклади пропорцiй.

5. Знайдiть невiдомий член пропорцiї:

 а) x : 100 =  35:2 ;      б) 325:100 =  х : 30 ;         в) 600:100 =125: x. 

Завдання групі

Завдання №1: У нормі фізіологічна втрата при пологах становить 0,5% від маси тіла. Визначити крововтрату в мл, якщо маса жінки 67 кг?

Розв’язання:

Відповідь: крововтрата склала 0,34 мл.

Завдання № 2: Визначити крововтрату при пологах, якщо вона склала 10 % ОЦК, при цьому ОЦК становить 5000.

Розв’язання: для визначення крововтрати при пологах, необхідно знайти, скільки становить 10 % від 5000.

Відповідь: крововтрата при пологах 500 мл.

 

 

ІV. Формулювання теми, мети й завдань заняття.

Мотивація навчальної діяльності студентів.

Для початку попрацюємо усно. Я буду зачитувати вам твердження, а ви повинні визначити, чи є воно істинним.

• Вік людини залежить від його зросту.
• Урожайність залежить від кількості корисних речовин у ґрунті.
• Кількість поганих оцінок залежить від кількості похмурих днів у році.
• Вартість квитка на автобус залежить від  кількості кілометрів, які вам потрібно проїхати.

Скажіть, будь ласка, на якому слові акцентується увага в кожному з даних тверджень? – Залежність.

Майже все, що відбувається з нами чи довкола нас, залежить одне від одного. На сьогоднішньому занятті ми з'ясуємо, як такі залежності ви­значаються в математиці та які математичні поняття з ними пов'язані.

 Однією з характерних особливостей нашого часу є те, що в усіх галузях практичної діяльності людини, навіть у таких традиційно   «нематематичних», як біологія, медицина, лінгвістика широко й ефективно застосовується математика. За допомогою математичного апарату людина описує природні явища на Землі, відкриває таємниці виникнення Всесвіту. Можна впевнено говорити, що математика – це могутній засіб пізнання явищ реального світу.

 Поняття функції є одним з найважливіших понять математики. Ідея функціональної залежності сягає в глибоку давнину, коли люди тільки почали розуміти існування різних видів залежності у природі. Як і інші, поняття функції виникло з потреб практики. У XVII — XVIII ст. з розвитком природознавства постала необхідність створення математичного апарату для опису різних процесів та явищ. Це привело до появи змінних величин.               Задовго до того, як були сформовані загальні поняття змінної величини і функції, їх графічно використовували в математиці. Для того щоб прийти до розуміння доцільності його введення й одержати перші досить чіткі означення, потрібні були зусилля відомих математиків декількох поколінь.

       Значну роль у розвитку цих понять відіграв метод координат французьких математиків П. Ферма (1601 — 1665) і Р. Декарта (1596 — 1650). Метод координат використовували для графічного дослідження функцій і розв'язування рівнянь. Це започаткувало потужний розвиток не тільки математики, а й природознавства.               Термін «функція» запровадив німецький математик Г. Лейбніц (1646 — 1716), який пов'язував її з графіком. Академік Петербурзької Академії наук Л. Ейлер (1707 — 1783) і швейцарський матем атик Й. Бернуллі (1667 — 1748) вважали функцію аналітичним виразом (формулою). Згодом Л. Ейлер узагальнив підхід до поняття функції як залежності однієї змінної величини від іншої. Цю ідею розвинули російський математик М. І. Лобачевський (1792 — 1856), німецький математик П. Діріхле (1805 — 1859) та інші вчені. Ініціатором введення поняття фунції у шкільний курс математики був відомий український математик Михайло Васильович Остроградський.

 Повторення й розширення відомостей про функцію

План

1. Означення функції. Основні поняття: аргумент, функція

2. Область визначення і множина значення функції.

3.Означення числової функції.

4.Способи задання функції

 

 Числовою функцією з областю визначення D називається за­лежність, при якій кожному числу х із множини D ставиться у відповідність по деякому правилу єдине число у із множини Е.

Змінна х називається незалежною змінною або аргументом функції, а змінна у — залежною змінною або функцією.

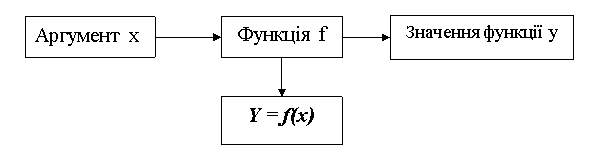
Функцію позначають латинськими буквами f, g, h... (або f(x), g(x), h(x)„.) або рівностями у = f(x), у = g(x), у = h(x)... Якщо задане конкретне значення незалежної змінної х = х₀, то у₀ = f(x₀) називається значенням функції f в точці х₀.

 Область визначення функції позначається D(f) (від анг. defi­ne — визначити). Множина, яка складається із всіх чисел f(x) таких, що х належить області визначення функції f, називаєть­ся областю значень функції і позначається E(f) (від анг. exist — існувати).               Областю визначення функції у = f(x), яка задана формулою, називається множина тих значень, які може приймати х, тобто формула має зміст (усі дії, вказані формулою, можна виконати). При знаходженні області визначення слід пам'ятати:

     1) Якщо функція є многочленом  у = а_n хⁿ + α_n-1 x^n-1 +... + α₁x + a₀,

то D(y) = (-; +) = R.

2) Якщо функція має вигляд у = , де f(x) і g(x) — многочлени, то слід вважати g(x)0 (знаменник дробу не дорів­нює 0).

3) Якщо функція має вигляд у = , то слід вважати f(x) > 0 (арифметичний квадратний корінь існує тільки з невід'ємних чисел).

Розглянемо приклад.

 Результати вимірювання температури тіла хворого в залежності від часу подано в таблиці:

 

Час доби х (год)	9	12	15	18	21	24
Температура тіла y=f(x) (С°)	39	38,5	38,3	37,3	37,1	37

 

 Залежність у·= f(x) є функцією, х — незалежна змінна, у — залежна змінна.

f(9) = 39, f(12) = 38.5,..., f(24) = 37.

D(f) = {9;12;15; 18; 21; 24}.

E(f) = {39; 38,5; 38,3; 37,3; 37,1; 37}.

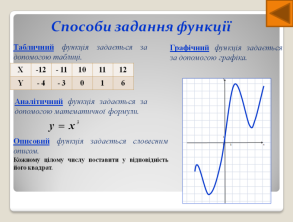 У математиці існує чотири способи задання функцій.

Аналітичний спосіб. Найчастіше функцію задають формулою, яка дає можливість одержати значення залежної змінної у, підставивши конкретне значення аргументу х.

Наприклад. Якщо кожному значенню х із множини дійсних чисел поставити у відповідність квадрат цього числа, то функ­цію можна записати у вигляді формули:

 у = х² або f(x)= x².

 Функціональну залежність між х і y можна виразити за допомогою деякого аналітичного виразу або формули. Ця формула і вказує на те, які дії (додавання, віднімання, множення, ділення, піднесення до ступеня, добування кореня, логарифмування, знаходження значень тригонометричних функцій тощо) і в якому порядку треба виконати над сталими числами і аргументом х, щоб для кожного його значення дістати цілком певне одне значення у.

 Приклади функцій, які ми наводили, це і є аналітично задані функції.

 Кожний аналітичний вираз, який містить х, має свою область визначення – це сукупність допустимих дійсних значень х, при яких заданий вираз набуває дійсних значень. Тому для функцій, які задано аналітично, розрізняють область визначення функції і область її значень.

Приклад .Якщо через х позначити радіус круга, а через у – його площу, то матимемо функціональну залежність, яка виразиться формулою:

у = π х²

Словесний спосіб. Часто закон відповідності між елементами двох множин описується за допомогою слів. Такий спосіб задавання функції називається словесним.

 Прикладом такої функції може бути функція у = sgn(x) (від латинського слова signum (“сигнум”), що означає “знак”).

 Тут кожному числу х>0 ставиться у відповідність число 1, числу х = 0 – число нуль і кожному числу х<0 – число – 1. Отже, кожному дійсному числу ставиться у відповідність одне дійсне число.

Графічний спосіб. Функцію можна задати також графічно. Графіком функції у = f(x) називається множина всіх точок пло­щини з координатами (x;f(x)) , де перша координата «пробігає» всю область визначення функції у = f(x), а друга координата — це відповідні значення функції в точці х.

Справді, візьмемо Декартову систему координат.

 

 

 

 

 

 

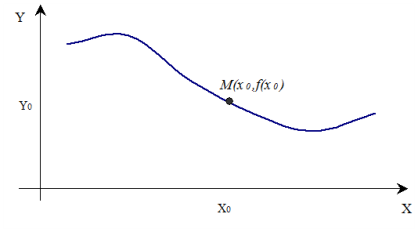
 Тоді для кожного значення х, яке належить області визначення функції, у площині x  y можна побудувати точку М з координатами х₀, f(x₀).Сукупність точок  M(x; f(x)) називають геометричним зображенням, або графіком функції у = f (x). У загальному випадку це буде якась лінія. Функція вважається заданою графічно, якщо задано її графік.

 У повсякденній діяльності середнього медичного працівника досить часто виникають практичні завдання, які на рівні теоретичного розв’язання можуть розглядатися як прикладні математичні, і якість їх розв’язування безпосередньо залежить від розвитку математичних компетентностей цих спеціалістів. Графічний спосіб задання фунцій зручний своєю наочністю. Дивлячись на графік, одразу можна з’ясувати властивості функції, яку він задає.

 Температурний лист хворого за виглядом схожий на координатну площину, де на осі Оу позначається температура від 34,0 до 42,00, а вісь Ох – дні перебігу захворювання на певну хворобу. Таким чином, температурна крива є функцією, вираженою графічно.

 Лікарі виявляють хвороби серця, вивчаючи графіки, отримані за допомогою кардіографа, їх називають кардіограмами. «Читаючи» такий графік, лікар діагностує роботу серця хворого.

Табличний спосіб. При експериментальних дослідженнях та спостереженнях залежність між величинами дуже часто подається у вигляді таблиць. Такий спосіб задання функції називається табличним. При табличному способі різним значенням аргументу відповідають певні значення функції. Прикладами табличного задавання функції можуть бути таблиці десяткових логарифмів, таблиці значень тригонометричних функцій, таблиці реєстрації температури хворого протягом дня тощо.

 Найчастіше табличним заданням функції користуються в медицині і біології, а саме тоді, коли закон залежності між величинами існує, але невідомий. У цьому разі проводять експеримент, за допомогою якого дістають ряд значень аргументу та відповідних значень функції. Одержані результати записують у вигляді таблиць. Таблиці не будуть  точно відображати функціональну залежність, тому що при вимірюванні, хочемо ми того чи ні, матимуть місце похибки, які залежать від класу точності приладів. У цьому полягає недолік табличного задання функції. Крім того, недолік табличного способу полягає ще й в тому, що ми можемо знайти в таблиці не всі, а лише окремі значення функції.

 Проте табличний спосіб зручний тим, що при такому задаванні ми без будь-яких обчислень маємо окремі значення функції. А це дуже важливо; іноді навіть функції, задані іншими способами, наприклад аналітично, зображають у вигляді таблиць. Такі таблиці широко використовуються на практиці в медицині.

 Крім того, за допомогою таблиць, методом лінійної інтреполяції можна, хоч і наближено, знайти ті значення функції, яких немає і в таблиці І, нарешті, при табличному задаванні легко будувати графіки функції, особливо тоді, коли графік будується по точках.

Огляд властивостей основних функцій.

Повторення і узагальнення властивостей вивчених видів функцій провести шляхом фронтальної бесіди і результати зане­сти в таблицю.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

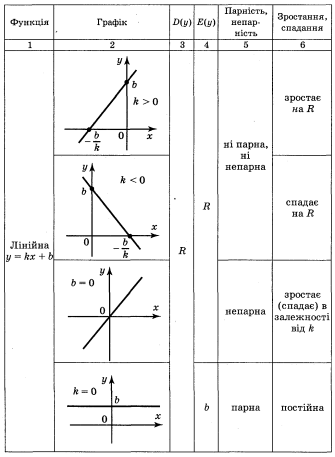
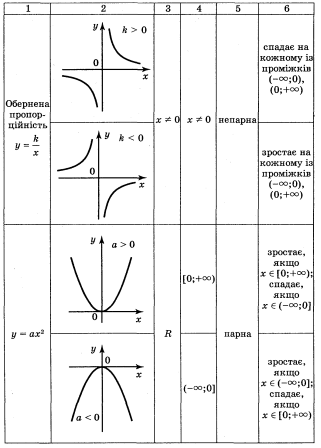
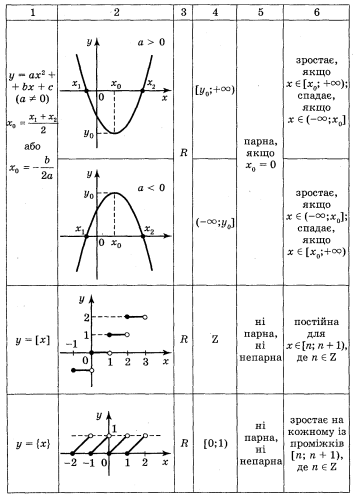
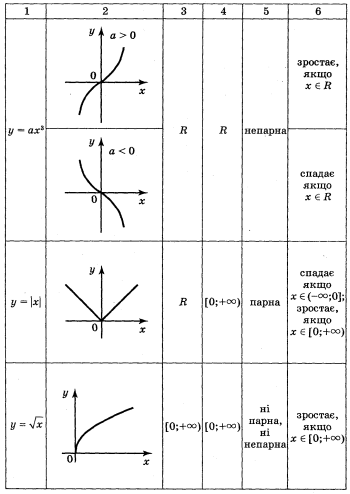
Виконання вправ

1. Знайдіть значення функції:

 a) f(x) = 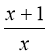у точках 1; -1; 5.

 

б) f(x) = у точках 3; 12; 52.

Відповідь: а) f(1) = 2, f(-1) = 0; f(5) = 1,2;

б) f(3) = 0; f(12) = 3; f(52) = 7

2. Функцію задано формулою у = x² на області визначення

D = {-3; -2; -1; 0; 1; 2; 3}. Задайте її за до­помогою:

а) таблиці;        б) графіка.

Відповідь:

a)	x	-3	-2	-1	0	1	2	3
	y	9	4	1	0	1	4	9

 

3. Знайдіть область визначення функції:

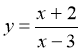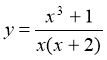а) у = х² + х³; б) ;  в) ;  д) ;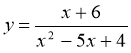

є) .

  Відповідь:

a) D(y) = R;  б) D(y) = (-; 3) (3; +);  в) D(y) = (-;-2) (-2;0) (0;+).

г) D(y) = (-; -3) (-3; 3) (3; +); д) D(y) = (-;l) (l;4) (4;+).

є) D(y) = [-6;+).

 

 

4. Знайдіть область значень функції:

а) у =  ;      б) у = -1.

Відповідь: а) Е(у) = [2; +);     б) Е(у) = [1; +).

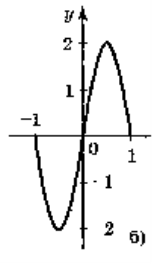
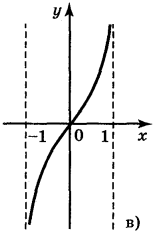
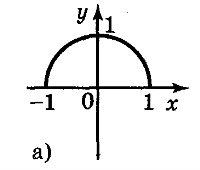
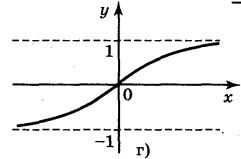
5. Для функцій, графіки яких зображено на рисунках, вкажіть D(y) і Е(у).

 

 

 

 

 

 

 

 

 

Відповідь:

а) D(у) = [-1;1]; Е(у) = [0;1]; б) D(y) = [-1;1]; E(y) = [-2;2];

в) D(y) = (-1;1); E(у) = R;     г) D(y) = R; Е(у) = (-1;1).

6. Які із ліній, зображених на рисунках, є графіком функції? Чому?

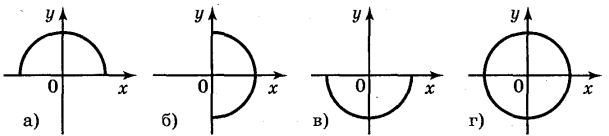
Відповідь: а); в).     

Функція y = f(x) буде задана коли:

1) задано область x визначення функції, тобто множину зміни аргументу x;

2) задано закон (правило), за яким встановлюється відповідність між елементами x і y.

V.  Закріплення нового матеріалу.

 

1. Усні вправи

                                

    

 

 

 

 

 

 

 

 

 

 

 

 

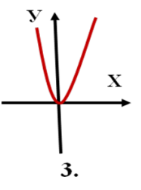
1. Графік якої функції зайвий?        

2. На якому рисунку зображено графік прямої  пропорційності?

3. На якому рисунку у графіка лінійної функції від’ємний кутовий коефіцієнт?

4. На якому рисунку у графіка лінійної функції

від’ємний коефіцієнт b?

 

 

 

2. Пауза-відпочинок. Розгадування кросворда.

Питання:

1.Чим частіше всього задають функціональні відповідності?

2.Яке слово у логіці розуміють під словом доказ, підстава?

3.Що є рівністю двох виразів?

4.Хто ввів поняття змінної величини і системи координат?

5.Хто уперше ввів слово «функція», що в перекладі «дія виконання»?

6.Яке інше значення має слово функція?

7.Що є графіком лінійної функції?

8.Як називається змінна n у виразі aⁿ?

9.Як називається число, яке підноситься до степеня?

 

 

 

 

 

 

3. Гра  “ Вірю - не вірю»

Лінійна функція – це функція, яку можна задати формулою у = kx + b,  де k – аргумент, х і b – дані числа.

1. Графіком лінійної функції є крива лінія.
2. Для побудови прямої, яка є графіком будь-якої лінійної функції достатньо знати координату однієї точки.
3. Лінійна функція – це функція, яка задається формулою

     у = kx + b,  де х – аргумент, k i b – дані числа.

4. Чи правильне твердження, що область визначення функції – це всі значення, які приймає аргумент функції?
5. Графік функції y = кх - пряма, яка не проходить через початок координат.
6. Якщо в лінійній функції більшому значенню аргументу відповідає менше значення функції, то така функція - спадна.

VI .Самостійна робота

              І варіант

1. Функцію задано формулою у = 15-х. Визначте:

 а) значення аргументу, при якому значення функції дорівнює -19;

 в) чи проходить графік функції через точку В(-2;-13).

2. Побудуйте графік функції 

Користуючись графіком знайдіть  значення функції, якщо значення аргументу дорівнює 2;

ІІ варіант

1. Функцію задано формулою у =-11+х. Визначте:

           а) значення функції, якщо значення аргументу дорівнює 6;

           в) чи проходить графік функції через точку А(-4;-15).

 2. Побудуйте графік функції 

Користуючись графіком знайдіть  значення аргументу, при якому значення функції дорівнює -1.

VII. Домашнє завдання:

 Г.П. Бевз, В.Г. Бевз Математика 10: К.: «Генеза», 2010.

Розділ 1, §4-5 ст. 30 № 161, 170, 178, 216

 

VIII. Підсумок заняття.

 Поглибили знання про функцію. Систематизували навички і уміння читати властивості функцій за їх графіком. Ознайомились із широким застосуванням функції. Найбільш активними сьогодні були… Оголошую оцінки.

 Заняття наше закінчується, ви повернетеся до звичайного життя. Але  незалежно від вашого бажання у ньому стикнетеся з графіками функцій, навіть не усвідомлюючи цього.

 

 

 

 

 

 

 

 

 

 

 

Література.

Основна:

 1. Г.П. Бевз, В.Г. Бевз Математика 10 клас : К.: «Генеза», 2010.

 2. Соколенко Л.О. Прикладна спрямованість шкільного курсу алгебри та початків аналізу: Навч. посібник. — Чернігів: Сіверянська думка, 2002.

 3.Лаврик В.І. Методи математичного моделюван¬ня в екології/ В.І. Лаврик — К.: Фітосоціоцентр, 1998

 4.Скафа, О. І. Методичні складові етапів формування понять у евристичному навчанні математики/ О. І.,Скафа// Математика в школі. — 2004. — № 1. — с.2—6.

 5. Соколенко Л.О. Прикладна спрямованість шкільного курсу алгебри та початків аналізу: Навч. посібник. — Чернігів: Сіверянська думка, 2002.-

 6. Соколенко О.І.  Особливості вик¬ладання вищої математики на природничих факуль¬тетах вищих навчальних закладів /   О.І.  Соколенко, 

Л.О. Соколенко// Вісник Чернігів¬ського державного педагогічного університету. - 2003.— Вип. 19. — (Серія: Педагогічні науки).

 Додаткова:

1. Святкіна К.А. Дитячі хвороби/ К.А. Святкіна, Є.В.Білогірська, Н.П.Кудрявцева. - М. : Медицина, 1988.-318 с.

2. Воробйова Г.М. Практикум з обчислювальної математики/ Г.М. Воробйова М.: -  Вища школа, 199.-

3. .Тихонов О.І. Аптечна технологія ліків/ О.І. Тихонов, Т.Г. Ярних – Вінниця: Нова книга, 2004 – 640 с.