Площа повної поверхні циліндра. Розв’язування задач.

Тема. Площа повної поверхні циліндра.

 Розв’язування задач.

Формування компетентностей:

предметна компетентність: домогтися засвоєння формул для обчислення площ бічної та повної поверхонь циліндра; сформувати вміння розв’язувати задачі, що передбачають застосування формул для обчислення площ бічної та повної поверхонь циліндра;

ключові компетентності:

• спілкування державною мовою – чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень;
• основні компетентності у природничих науках і технологіях – розпізнавати проблеми, що виникають у довкіллі і які можна розв’язати засобами математики;
• соціальна та громадянська компетентності – висловлювати власну думку, слухати й чути інших.

Тип заняття: комбінований урок.

Обладнання. Роздатковий матеріал. Таблиці, набір моделей циліндра, мультимедійна система, комп’ютер.

Епіграф заняття:

Геометрія безмежно різноманітна

 і міститься в усьому.

М. Яругін

Хід заняття.

I. Організаційний момент.

Перевірка присутності студентів, наявність форми одягу.

 

 II. Актуалізація опорних знань.

1. Перевірка домашнього завдання.

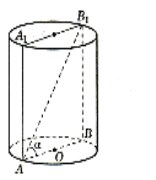Задача 1. Діагональ осьового перерізу циліндра дорівнює d і нахилена до площини основи під кутом . Знайдіть висоту, діаметр основи та радіус основи циліндра.

Розв’язання. Нехай АВВ₁А₁ – осьовий переріз циліндра, АВ₁ – його діагональ і В₁АВ = . Трикутник АВВ₁ – прямокутний, тому висота циліндра ВВ_{1 =}               , а діаметр основи АВ =           . Радіус основи ОА = 0,5           .

Розв’язання. Нехай АВВ₁А₁ – осьовий переріз циліндра, АВ₁ – його діагональ і В₁АВ = . Трикутник АВВ₁ – прямокутний, тому висота циліндра ВВ_{1 =} dsin, а діаметр основи АВ = dcos.

Радіус основи ОА = 0,5d cos.

Задача 2. Циліндр радіусом і висотою 5 перетинається площиною, паралельною осі циліндра і віддаленою від неї на 1. Знайдіть площу і периметр перерізу.

Розв’язання. Нехай переріз АВВ₁А₁ циліндра віддалений від осі ОО₁ на ОС = 1.

Тоді АС = =

Шукана площа перерізу S = AA₁  AC  2 = 5  3  2 = 30, а периметр перерізу

P = 2(AA₁ + АВ) =

Розв’язання. Нехай переріз АВВ₁А₁ циліндра віддалений від осі ОО₁ на ОС = 1.

Тоді

Шукана площа перерізу S = AA₁  AC  2 = 5  3  2 = 30, а периметр перерізу

P = 2(AA₁ + АВ) = 2(5 + 6) = 22.

 

 

2. Тест-розминка

1. Як називається тіло утворене обертанням прямокутника навколо його сторони:

А) кругом       Б) конусом      В) циліндром

2. Якщо прямокутник обертається навколо осі, його сторони описують

А) рівні трикутники

Б) рівні кути, які лежать на паралельних площинах

В) рівні квадрати

3. Як називають такий круг?

А) основою конуса    Б) основою циліндра     В) колом

4.Сторона АВ, паралельна осі циліндра,описує криву поверхню, яку називають ….

А) кругом   Б)прямокутником   В) бічною поверхнею циліндра

5. Кожний відрізок бічної поверхні, що дорівнює АВ – це..

А) радіус кута основи циліндра

Б) твірна циліндра

В) діагональ прямокутника.

6. Довжина твірної DC – це ..

А) діагональ прямокутника      Б)висота циліндра    В) радіус кута

3. Кросворд. (Пропоную вам розгадати кросворд, пригадавши означення деяких елементів циліндра).

			7
		1
	2
	3
	4
			5
			6

 

			7Ц
		1в	И	с	о	т	а
	2к	о	Л	о
	3т	в	І	р	н	а
	4о	с	Н	о	в	и
			5Д	о	т	и	ч	н	а
			6Р	а	д	і	у	с

 

По горизонталі

1. Відстань між площинами основ циліндра. (Висота)
2. Геометрична фігура, що складається з усіх точок площини, рівновіддалених від даної точки. (Коло)
3. Відрізок, що сполучає відповідні точки кіл основ циліндра. (Твірна)
4. Два круги, з яких складається циліндр. (Основи)
5. Площина, яка проходить через твірну циліндра і перпендикулярна до площини осьового перерізу, що містить цю твірну. (Дотична)
6. Будь-який відрізок, що сполучає центр основи циліндра з точкою на колі його основи. (Радіус)

По вертикалі:

7. Тіло обертання, отримане в результаті обертання прямокутника навколо його сторони як осі. (Циліндр)

У виділеному стовпчику: ЦИЛІНДР.

 

 4. Усне опитування.

1. Що називається циліндром?
2. Який циліндр називається прямим?
3. Назвати на малюнку твірні, вісь, радіус циліндра.
4. Які властивості мають:

а) основи циліндра; (рівні і паралельні)

б) твірні циліндра. (рівні і паралельні)

5) Яке розміщення осі ОО₁ циліндра щодо:

а) його основ; (перпендикулярна)

б) його твірних; (паралельна)

в) його радіусів. (перпендикулярна)

 

III. Мотивація навчальної діяльності.

Як вам відомо геометрія виникла ще в далекій давнині, коли людям довелося займатись вимірюванням відстаней, обчислювати площі геометричних тіл різноманітної форми і різних розмірів, обчислювати місткість різних споруд, посудин, деталей.

Навколишні предмети ми можемо вивчати по різному.

Проте вивчаючи геометрію, ми не цікавимося, з якого матеріалу зроблено навколишні предмети, якого вони кольору, в якому вони стані. При вивченні геометрії нас цікавлять форми і розміри предметів.

Як сказав видатний французький архітектор Лє Корбюзьє: «Ми живемо в геометричний період і навкруги нас – геометрія»

І справді, світ, в якому ми живемо, наповнений геометрією будинків і вулиць, творіннями природи й людини. Геометрія є могутнім інструментом пізнання природи і створення техніки. Вона виявляється скрізь, де потрібна найменша точність у визначенні форми і розмірів. Техніку, інженеру, робітнику, архітектору і вам майбутнім медикам –  необхідна геометрична уява. Багатогранники знаходять широке застосування у повсякденному житті, науці і техніці.

Сьогодні ми продовжимо наше знайомство з тілами обертання та розглянемо як обчислюється площа бічної і повної поверхонь  циліндра.

Якщо озирнутися навколо, то можна побачити багато предметів циліндричної форми. Це і

• пробірки,
• медичні шприци,
• косметичні товари,
• різноманітні автомобільні деталі тощо.

На практиці часто виникає потреба знати їх площі поверхонь.

 

IV. Пояснення нового матеріалу.

План.

1. Площа бічної та повної поверхонь циліндра.

2. Розв’язування задач.

 

Якщо поверхню циліндра розрізати по колах основ і по одній із твірних, а потім розгорнути на площині, то дістанемо розгортку циліндра.

Вона складається з прямокутника – розгортки бічної поверхні – та двох різних кругів. Якщо радіус основи циліндра дорівнює r (його називають радіусом циліндра), а висота – h, то його бічна поверхня розгортається в прямокутник зі сторонами 2πr і h. Площа цієї розгортки є площею бічної поверхні циліндра:

S_б = 2πRH

Щоб знайти всю площу поверхні циліндра S_ц, досить до площі бічної поверхні додати площі двох його основ:

S_ц  = 2πRH + 2πR², або S_ц  = 2πR(H + R)

V. Розв’язування задач.

Задача . (Розв’язати задачу усно).

(Умова задачі та рисунок відображені на екрані).

 

а) BD = 10 см,

    H = 8 см,

Знайти: R

 

б) ABCD – прямокутник,

    АВ = 10 см,

    AD = 6 см.

Знайти: S_б.

 

 в) ABCD – квадрат,

     BD =  см

Знайти: S_п.

 

VІ. Практична робота.

Хочу запропонувати вам цікаву практичну роботу на обчислення площ поверхонь циліндра. Кожна пара студентів одержує міні-модель циліндра (всі моделі різної величини). Необхідно виміряти потрібні елементи цього циліндра для здійснення обчислень.

Студенти працюють парами і через визначений час віддають аркуші з розрахунками. Після цього на м/дошці висвітлюються вірні результати для самоперевірки.

 

№	R	H	Sосн	Sп	Sб
1	4.5	22	20,25	238,5	198
2	305	15,5	12,25	133	108,5
3	2,5	11,5	6,25	70	57,5
4	3,5	13	12,25	115,5	91
5	3,5	20	12,25	164,5	140
6	3,5	18,5	12,25	154	129,5
7	4	22	16	208	176
8	3,5	15	12,25	129,5	105
9	3	10	9	78	60
10	1,8	7	3,24	31,68	25,2
11	5	18	25	230	180
12	2,5	13,5	6,25	80	67,5
13	4	15	16	152	120
14	4	14	16	144	112
15	3,5	13	12,25	115,5	91

 

- Рене Декарт сказав:

… У математичних науках є дуже вдалі винаходи, здатні принести велику користь, задовольняючи любов до знань, полегшуючи всі ремесла і скорочуючи працю людини.
                                  

 Р. Декарт

VII. Розв’язування задач прикладного змісту.

 

Задача.

 

Скільки квадратних сантиметрів бинту в рулоні ширина і радіуси якого дорівнюють відповідно 8 см, 2см і 4 см? Товщина бинту 0,2 мм.

 

 

 

 

 

Задача.

У циліндричну посудину діаметром 10см опущено тіло складної конфігурації. Визначити об’єм тіла, якщо рівень рідини в посудині піднявся на 4см.

 

- Кожне червоне кров’яне тільце або, як кажуть, «кулька», може поглинати та виділяти кисень тільки з поверхні. Тому фізіологічне функціонування кульок крові  має бути тим успішніше, чим більша їх загальна поверхня. А вона тим більша, чим дрібніше роздроблена їх речовина і чим більше, відповідно, їх число.

Задача.

Фізіологи, на основі приблизного визначення поверхні кожної кульки в крові людини, а також приймаючи до уваги, що в 1мм³ крові у людини міститься 5000000 кульок і що кількість крові дорослої людини дорівнює приблизно 5л, обчислили загальну поверхню всіх червоних кульок, які містяться в крові людини.

Обчисліть загальну поверхню всіх червоних кульок, які містяться у крові людини, знаючи, що кожна кулька насправді (всупереч назві) має форму гральної шашки шириною 0,007 мм, а товщиною 0,002мм.

Задача.

Золотих справ майстер позолотив усередині 7однакових циліндричних стаканів. Діаметр дна стакана 6 см, а глибина – 10 см. Скільки використано золота на позолоту стаканів і скільки коштує це золото, якщо на кожен 1 см² поверхні пішло 0,026 г золота і 1 г золота оцінюється приблизно в 500 гривень?

 

 

 

VIII. Самостійне розв’язування задач.

 

Розв’язати завдання і вказати варіант відповіді у вигляді букви.

 

Варіант І.

1. Відрізок АА₁ є :

А) вісь;

Б) висота;

В) твірна;

Г) радіус.

 

2. Якщо радіус основи R, то довжина кола основи l дорівнює:

А) 2R;

Б) R;

В) R²;

Г) 4R.

 

3. Знайти S_осн. якщо R=5.

А) 5;

Б) 25V;

В) 10;

Г) 20.

 

4. Знайти S_б, якщо R=4, Н=8.

А) 32;

Б) 32;

 

В) 12;

Г) 64.

5. Знайти V, якщо R=2, Н=4.

А) 6;          В) 16;

Б) 8;           Г) 16.

 

	А	Б	В	Г
1	Ю	Б	П	У
2	Р	С	М	Ч
3	И	А	Ж	О
4	Р	А	І	Ц
5	Х	Ф	Я	Щ

 

 

 

 

Варіант ІІ.

1.  Відрізок ОО₁ є :

 

А) вісь;

Б) висота;

В) твірна;

Г) радіус.

 

 

 

 

2. Знайти довжину кола основи l, якщо R=2.

А) 2;

Б) 4;

В) 8;

Г) 4.

 

 

3. Знайти S_о, якщо R=6.

А) 6;

Б) 36;

В) 12;

Г) 36.

 

4.Знайти V, якщо R=4, Н=5.

А)80;

Б) 9;

В) 20;

Г) .

5. Знайти S_б, якщо  R=5, H=6.

А) 30;

Б) 11;

 

В) 60;

Г) 30.

 

	А	Б	В	Г
1	У	К	Е	Н
2	Г	С	Ш	З
3	Ф	П	В	А
4	І	Р	О	Л
5	Д	Я	Х	М

 

 

 

 

 

 

 

IХ. Виступ про циліндр у контексті прикладної спрямованості

підготувала студентка математичного гуртка

Поняття про циліндричну форму виникло ще у стародавні часи.   

Таку форму вважали гармонійною та досконалою. Грецький філософ Анаксімандр (бл. 610-бл. 540 до н.е.) у своїй космологічній теорії стверджував, що Земля має форму циліндра. Назва циліндр – грецького походження і означає вал, каток.

Членів математичного гуртка зацікавило питання: «Чому циліндрична форма характерна для великої кількості предметів оточення, створених вже не лише природою, а й людиною?»

Циліндрична форма у реальному світі є однією з найпоширеніших. Розглянемо приклади в живій природі. Дослідження симетрії біоструктур на молекулярному і надмолекулярному рівнях дозволило заздалегідь визначати різноманітні зовнішні форми і внутрішні будови будь-яких організмів. Серед мікроорганізмів циліндрична форма спостерігається у паличкоподібних вірусів. Форма тулуба тварин також наближається до циліндричної. В індіанців Перуанських Кордильєрів майже циліндрична грудна клітка, об’єм якої може перевищувати 12 000 см³, щоб розмістити легені з високою пропускною здатністю (що зумовлено тим, що місцеве населення Високих Анд протягом багатьох поколінь переживало процес акліматизації).

Стебла багатьох рослин також циліндричної форми. Довжина стебел від 1-1,5 мм (прісноводна вольфія) до 300 м (тропічні пальми-ротанги), діаметр сягає від частини міліметра (мохи) до 11 м(баобаб). У тянь-шанської ялини крона у формі циліндра. На півострові Сомалі величезні термітники – звичайна картина. Циліндрична башта досягає у висоту 4,5м. Найвищий термітник знайдено в Африці. Його висота 12,8 м, а в діаметр сягав усього

3 м. Товщина стінок у термітниках сягає 8-10 см.

У спорті теж використовують предмети у вигляді циліндра. Ворота у хокеї зроблені з циліндричних труб. Наявність циліндричних  у спортивних снарядів (шести для лазіння, турніки, спортивні бруси, штанги та ін.) пояснюється тим, що вони не мають ребер, а тому зручні для охоплення рукою.

Досить багато продуктів харчування роблять циліндричної форми. Наприклад, торти, цукерки, тверді сири. Їх форма, як і форма різноманітних посудин, наприклад, каструль, банок, форм для тортів тощо, обумовлена зручністю, економічністю у використанні.

Спосіб обчислення бічної поверхні та об’єму циліндра знайшов ще Архімед. Об’єм циліндра в стародавні часи обчислювали множенням площі основи на висоту. Але це правило було знайдено не внаслідок теоретичних міркувань, а виведено на основі практики, обчислюючи об’єм вмісту бочки, в якій містилося вино.

 У глибокій давнині вважалося, що довжина кола в 3 рази довша його  діаметру. Ці дані містяться в клинописних таблицях Стародавнього Межиріччя. Архімед в 3 ст. до н.е. можливо перший запропонував математичний спосіб обчислення числа пі, яке застосовується в формулах для обчислення бічної поверхні і об’єму циліндра.

Циліндричні форми часто зустрічаються  в архітектурі. В архітектурній композиції величного Парфенону в Греції, Казанського собору в С.-Петербурзі, башти Тауера і Великій Британії, каплиці Темп’єтто в Італії можна виділити велику кількість деталей циліндричної форми. Присутність такої форми здебільшого пояснюють естетичними міркуваннями. Але це не так.

Цікаво те, що зі всіх призматичних і циліндричних тіл з даною поверхнею найбільший об’єм має прямий круговий циліндр, основа якого дорівнює 1/6 повної поверхні. Цей математичний факт привів до того, що певний час деякими архітекторами пропагувалась ідея побудови будинків циліндричної форми. Такі будинки мали перевагу, крім економії будівельного матеріалу, ще й тому, що менша поверхня зовнішніх стін означає менші втрати тепла зимою, стіни менше будуть нагріватися влітку. Радіальне розташування кімнат скорочує переходи з однієї кімнати в іншу, що особливо цінується у великих будівлях установ і готелів. Так, в Італії, в Сестріфі, побудовано готель Дукі д’Аоста діаметром 25 і висотою 47 м; у Франції тоді було споруджено багатоповерховий будинок циліндричної форми.

Можна також згадати про такі форми і у мистецтві. «На рубежі 1900-1910 рр. художник Малевич Казимир Северинович (1878-1935) створював близькі до кубізму, але насичені інтенсивним кольором композиції, в яких предметна форма конструювалась із циліндричних  та конусовидних елементів».

Серед медичних речей є чимало таких, що мають циліндричну форму. Це крапельниці, шприци, таблетки, пробірки, рулони вати тощо.

Кровоносні судини, спинний мозок, кров’яні тільця мають циліндричну будову.  Кожне червоне кров'яне тільце або, як кажуть, «кулька», може поглинати та виділяти кисень тільки з поверхні. Кожна кулька насправді (всупереч назві) має форму гральної шашки шириною 0,007 мм, а товщиною 0,002 мм.

Тому фізіологічне функціонування кульок у крові тварини має бути тим успішніше, чим більша їх загальна поверхня. А вона тим більша, чим дрібніше роздроблена їх речовина і чим більше, відповідно, їх число. Фізіологи, на основі приблизного визначення площі  поверхні кожної кульки в крові людини, а також приймаючи до уваги, що в 1 мм³ крові у людини міститься 5000000 кульок і що кількість крові у дорослої людини дорівнює приблизно 5 л, обчислили, що загальна поверхня всіх червоних кульок, які містяться у крові людини, дорівнює 3200 м².

 

 

ХI. Підсумок заняття та оцінювання студентів.

Сьогодні ми повторили означення, основні властивості та формули для обчислення площі поверхні та об’єму циліндра, застосували ці знання при розв’язуванні задач прикладного змісту.

І як підсумок до заняття хочу нагадати вам слова мистецтвознавця, доктора філософських наук Олександра Вікторовича Волошина «Математика прекрасна сама по собі, але, коли вона несе цю красу в розвиток цивілізації, це стає пошуком досконалості».

 

ХІІ. Домашнє завдання. 

Бевз Г.П. 11 клас - §31 вправи №1009, 1012, 1024.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Література:

1. Бевз Г.П. Математика: 11кл. : підруч. для загально освіт. навч. закл. : рівень стандарту – К. : Ґенеза, 2011.
2. Погорєлов О.В. Геометрія. 10-11 кл. – К. : Освіта, 2001.
3. Солодченко Л.І. Розвиток життєвих компетентностей на уроках математики. – Тернопіль-Харків: Ранок, 2011.
4. Кованцов М.І. Математична хрестоматія. - К. : Радянська школа, 1977.
5. Бевз Г.П. Методика розв’язування стереометричних задач. – К. : Радянська школа, 1988.
6. Все для вчителя: К.: січень 2011.