Числові нерівності. Доведення числових нерівностей.

Тема уроку. Числові нерівності. Доведення числових нерівностей.

Мета уроку: домогтися засвоєння учнями змісту: означення, що виражає залежність між співвідношеннями >,<,= і знаком різниці лівої та правої частин нерівності; поняття числової нерівності та уявлення про види числових нерівностей; поняття «довести нерівність» та алгоритму доведення нерівностей. Виробити вміння: відтворювати зміст вивчених понять і алгоритмів та застосовувати їх для розв'язування вправ на порівняння числових та буквених виразів і вправ на доведення нерівно­стей у найпростіших випадках.

Тип уроку: засвоєння знань, вироблення вмінь.

Наочність та обладнання: опорний конспект.

Хід уроку

І. Організаційний етап

Учитель розповідає про особливості вивчення алгебри й органі­зацію навчального процесу в 9 класі, наголошуючи на необхіднос­ті підготовки до державної підсумкової атестації; аналізує будову підручника.

ІІ. Перевірка домашнього завдання

Учитель перевіряє літнє домашнє завдання (якщо таке було задано).

III. Формулювання мети і завдань уроку.

Мотивація навчальної діяльності учнів

Для усвідомлення учнями необхідності вивчення основного питання уроку (означення, що виражає залежність між співвід­ношеннями >, <, = і знаком різниці лівої та правої частин нерів­ності), пропонуємо таке завдання.

Завдання

Визначте, який із записів зайвий. Відповідь обґрунтуйте.

1. 25 > 17; 0,32 < 0,4; 0,5 = 1,4 – 0,9;
2. 25 > 17; 0,32 < 0,4; 0,5 < 1,4 – 0,9.

Після обговорення з учнями результатів виконання запропо­нованого завдання формулюється такий висновок: у 7 класі було вивчено питання про види, властивості й способи перетворення виразів, що не містять ділення на змінну (цілі вирази); у 9 класі настав час вивчити способи порівняння виразів. Цей висновок і є по суті основною дидактичною метою всього розділу.

IV. Актуалізація опорних знань та вмінь учнів
Усні вправи

1. Порівняйте числа:

1) 6,09 і 6,9; 2) 13 і 13; 3) -11,4 і -10,4.

2. Порівняйте вирази:

1) (-3)¹⁴ і (-3)¹³; 2) (-2,4)¹⁵ і (-3,1)¹⁸; 3) -2,4¹⁶ і (-2,4)¹⁶.

3. Знайдіть різницю чисел 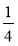і 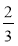і порівняйте її з нулем.
4. Яке з чисел лежить праворуч на числовій осі:

1) -24 чи 12; 2) -3 чи -8;  3) -0,5 чи -0,8; 4) чи ?

5. Подайте у вигляді квадрата двочлена вираз:
   1) у² + 2у + 1;  2) а² – 10а + 25; 

3) m² + 6m + 9;  4) а – 2+ b (а ≥ 0, b ≥ 0).

V. Формування знань

План вивчення нового матеріалу

1. Означення, що виражає залежність між співвідношення­ми >, <, = і знаком різниці лівої та правої частин нерівно­сті.
2. Види числових нерівностей.
3. Алгоритм доведення числових нерівностей.
4. Приклад доведення числової нерівності.

Опорний конспект № 1

Методичний коментар

Вивчення матеріалу уроку починається з формулювання за­гального означення понять «більше», «менше» або «дорівнює», яке є узагальненням правил порівняння різних видів дійсних чисел, які було вивчено протягом попередніх років навчання в школі. При ви­вченні цього питання слід наголосити на тому, що сформульоване означення є універсальним, тобто може бути використане не тільки для порівняння будь-якого виду чисел, але й для порівняння вира­зів (перед формулюванням означення на етапі актуалізації опорних знань та вмінь доцільно виконати з учнями усні вправи, див. вище).

Після формулювання означення вчитель має провести роботу зі систематизації знань учнів про види нерівностей: вони поді­ляються за знаком та за змістом (див. опорний конспект № 1). При цьому можна провести паралелі з видами числових рівностей (до речі, такі паралелі бажано проводити і під час вивчення влас­тивостей числових нерівностей), тобто учні мають усвідомити, що нерівності, так само, як і рівності,— це записи певного виду, але за змістом вони поділяються на правильні та неправильні.

З розгляду видів нерівностей цілком логічно випливає питання про доведення того факту, що дана нерівність є правильною (або визначення правильності чи неправильності даної нерівності). Та­ким чином формулюється уявлення учнів про зміст поняття «до­вести нерівність», а також про послідовність дій для доведення нерівності (алгоритм доведення нерівності), яка далі ілюструється відповідним прикладом на доведення числової нерівності.

VI. Формування вмінь

Усні вправи

1. Порівняйте з нулем різницю правої та лівої частин нерівності:

1) х < у; 2) а ≥ b; 3) 3 > х; 4) т ≤ 2.

2. Відомо, що т > п. Чи може т – п дорівнювати:

1) -3;  2) 0;  3) 0,3; 4) а²?

3. Порівняйте числа m і n, п і р, т і р, які зображені точками на координатній прямій (див. рисунок).

Письмові вправи

Для реалізації дидактичної мети уроку слід розв'язати вправи такого змісту:

1. порівняти числа за даним значенням їхньої різниці;
2. зобразити числа на координатній прямій, враховуючи дані про їх порівняння;
3. порівняти дійсні числа за означенням;
4. порівняти вирази при різних значеннях змінних;
5. довести нерівності (найпростіші випадки).

Методичний коментар

Для кращого засвоєння учнями змісту матеріалу уроку ре­комендується при виконанні відповідних вправ неодноразово по­вторювати означення (включаючи також і умову рівності чисел). Важливо відпрацювати вміння виконувати порівняння чисел че­рез геометричні уявлення в прямому і зворотному порядку (одне число більше за друге, якщо воно лежить на координатній прямій правіше, і навпаки, якщо число лежить правіше на координатній прямій, то воно більше). При відпрацюванні вмінь застосовувати алгоритм доведення числових нерівностей слід вимагати від учнів чітких і послідовних записів у зошитах та докладних коментарів при усних поясненнях. Оскільки даний урок є першим у цій темі, то на ньому розв'язуються вправи на доведення нерівностей, які передбачають отримання певного числового значення різниці лівої та правої частин нерівності (більш складні випадки, що передба­чають виділення повного квадрата, або інші способи визначення знака різниці лівої та правої частин нерівності, будуть розглянуті на наступному уроці).

VII. Підсумки уроку

Контрольні запитання

1. Заповніть пропуски:

1) т > п, якщо т ... п ... 0;

2) х < у, якщо х ... у ... 0;

3) х ... у, якщо х – у = 0.

2. Що означає запис:
   1) a > b; 2) c < d?

VIII. Домашнє завдання

1. Вивчити означення понять, розглянутих на уроці.
2. Розв'язати вправи: на порівняння чисел за даним значенням їхньої різниці; порівняння дійсних чисел за означенням; до­ведення нерівностей (найпростіші випадки).
3. Повторити: формули скороченого множення (зокрема квадрат двочлена), властивості степеня з парним і непарним натураль­ним показником.