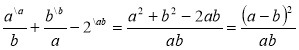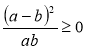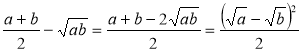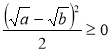Числові нерівності. Доведення числових нерівностей.
Тема уроку. Числові нерівності. Доведення числових нерівностей.
Мета уроку: домогтися засвоєння учнями змісту: додаткових нерівностей для суми взаємно обернених додатних чисел та середнього арифметичного двох невід'ємних чисел (у порівнянні з їх середнім геометричним) та доведення цих нерівностей; способу застосування доведених нерівностей при доведенні інших числових нерівностей. Продовжити роботу з вироблення вмінь: відтворювати зміст вивчених понять і алгоритмів та застосовувати їх для розв'язування вправ на порівняння числових і буквених виразів, а також вправ на доведення нерівностей у найпростіших випадках і випадках, що передбачають застосування означення і перетворення різниці лівої та правої частин нерівності, яку треба довести з використанням виділення квадрата двочлена.
Тип уроку: закріплення знань, вироблення вмінь.
Наочність та обладнання: опорний конспект.
Хід уроку
І. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
Виконання вправ домашньої роботи перевіряється ретельно в учнів, що потребують додаткової педагогічної уваги (учитель збирає їхні зошити на перевірку).
Фронтальну перевірку якості виконання вправ домашньої роботи можна провести у формі гри «Знайди помилку».
III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Створенню відповідної мотивації на уроці може посприяти виконання учнями такого завдання.
Завдання
Порівняйте два вирази, якщо відомо, що а > 0, b > 0, а різниця першого і другого виразів дорівнює:
1) 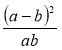 ; 2)
; 2) 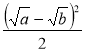 .
.
Після обговорення результатів, отриманих у ході виконання запропонованого вище завдання, сумісними зусиллями приходимо до висновку: порівняння виразів шляхом визначення знака різниці двох виразів та застосування означення порівняння чисел можна проводити, навіть коли різниця є буквеним виразом, що містить квадрат двочлена. Вивчення цього питання і є основною дидактичною метою уроку. Завдання на урок логічно випливають із цієї мети: сформулювати загальне правило, а також навчитися застосовувати це правило для розв'язування задач на доведення нерівностей.
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
- Порівняйте числа а і b, якщо:
1) а – b = -5; 2) а – b = 4,5; 3) а – b = -19,8;
4) b – а = -0,1; 5) а – b = 0.
- Подайте у вигляді квадрата двочлена вираз:
1) х2 – 2х + 1; 2) т2 + 10т + 25; 3) х2 – 6т + 9;
4) т2 – тп + п2 – тп; 5) х – 2![]() + у (х > 0; у > 0).
+ у (х > 0; у > 0).
- Порівняйте з нулем значення виразу:
1) т2; 2) т2 + 1; 3) (т + 1)2; 4) т2 + 2тп + п2 + 1.
V. Формування знань
План вивчення нового матеріалу
-
Доведення нерівності
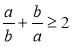 , а > 0, b > 0.
, а > 0, b > 0.
-
Доведення нерівності
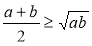 , а ≥ 0, b ≥ 0.
, а ≥ 0, b ≥ 0.
- Приклади застосування доведених нерівностей.
Опорний конспект № 2
|
Доведення нерівностей |
|
1. Довести нерівність: |
|
Доведення. Знайдемо різницю лівої та правої частин нерівності:
Сума додатних взаємно обернених чисел не менша за 2. |
|
Зауваження: рівність має місце при а = b. |
|
2. Довести нерівність: |
|
Доведення. Знайдемо різницю лівої та правої частин нерівності:
|
|
Зауваження: рівність має місце лише при а = b або а = b = 0. |
|
Приклад. Доведемо нерівність |
|
Доведення. Подамо вираз |
Методичний коментар
Доведення нерівностей шляхом застосування нерівностей для середнього арифметичного двох невід'ємних чисел і через порівняння з нулем виразу, що дорівнює різниці лівої та правої частин нерівності, з попереднім виділенням квадрата двочлена з утвореного виразу є одним із питань, які передбачені програмою з математики і мають досить широке практичне застосування. Саме тому вже на даному, другому, уроці, присвяченому вивченню способів доведення нерівностей, розглядаються питання:
- про доведення нерівностей у випадку, коли різниця лівої та правої частин нерівності є виразом, що містить букви;
- про застосування для доведення нерівностей співвідношень між середнім арифметичним та середнім геометричним двох невід'ємних чисел і сумою двох взаємно обернених додатних чисел.
Для успішного сприйняття матеріалу уроку на етапі актуалізації опорних знань та вмінь учнів рекомендується виконати усні вправи на порівняння з нулем буквеного виразу та на повторення формул скороченого множення, зокрема квадрата двочлена (див. вище). Після розв'язання цих вправ цілком логічним є доведення нерівності для суми двох додатних взаємно обернених чисел і для середнього арифметичного та середнього геометричного двох невід'ємних чисел (під час доведення акцентуємо увагу учнів на те, що при порівняння з нулем різниці лівої та правої частин нерівності виділяємо квадрат двочлена). Також важливо звернути увагу учнів на те, що крім ілюстрації загального способу доведення нерівностей (шляхом виділення квадрата двочлена у виразі, що поданий як різниця лівої та правої частин даної нерівності) доведені нерівності можуть бути використані як засіб доведення інших нерівностей. Для цього розглядається приклад, що ілюструє спосіб міркувань при розв'язуванні подібних прикладів.
VI. Формування вмінь
Усні вправи
- Порівняйте числа а і b, якщо:
1) а – b = т2; 2) а – b = (m + 1)2; 3) а = ![]() ; b =
; b = ![]() ; т ≥ 0.
; т ≥ 0.
- Виділіть повний квадрат у виразі:
1) b2 – 2bс + с2; 2) 4b2 – 4bс + с2; 3) -4b2 + 4bс – с2; 4) -4b2 + 4b – 2.
Письмові вправи
Для реалізації дидактичної мети уроку слід розв'язати вправи такого змісту:
- довести нерівності (з використанням виділення квадрата двочлена з виразу, що дорівнює різниці лівої та правої частин даної нерівності);
- довести нерівності (з використанням доведених опорних нерівностей).
Методичний коментар
Відповідно до мети уроку проводиться робота для вироблення вмінь доводити нерівності з використанням означення (див. алгоритм, складений на попередньому уроці), а також уміння застосовувати доведені нерівності для доведення нерівностей (оскільки цей матеріал вимагає від учнів достатнього та високого рівнів знань і вмінь, то обов'язковим він є тільки для учнів відповідного рівня навчальних досягнень).
VII. Підсумки уроку
Контрольні завдання
- Заповніть пропуски:
1) т + ... > 2, т > 0; 2) ![]() , т ≥ 0, n ≥ 0.
, т ≥ 0, n ≥ 0.
- Порівняйте вирази тіл, якщо:
1) т – п = а2; 2) т – п = а2 + 4;
3) т – п = а2 – 2а + 1; 4) т – n = а2 – 2а + 2.
VIII. Домашнє завдання
- Вивчити схему доведення нерівностей, розглянутих на уроці.
- Розв'язати вправи: на доведення нерівностей, подібних до розглянутих на уроці.
- Повторити властивості числових рівностей [7, табл. 4].


про публікацію авторської розробки
Додати розробку