Числові послідовності
Тема уроку: Числові послідовності. Розв’язування задач.
Мета уроку:
-навчальна: повторити, узагальнити та систематизувати теоретичні знання учнів за темою «Арифметична та геометрична прогресії»; перевірити вміння використовувати отримані знання під час розв’язування задач;
-розвивальна: розвивати логіку, пам’ять, нестандартність мислення, вміння узагальнювати та порівнювати;
-виховна: виховувати інтерес, навички колективної роботи.
Тип уроку: узагальнення та систематизації знань.
Хід уроку :
■ I. Організаційний етап
▪ Привітання
▪ Перевірка присутності учнів: кількість за списком ______, кількість присутніх на уроці ________, відсутніх _______
▪ Перевірка готовності учнів та кабінету до уроку
Відкрили зошити, записали число, класна робота. Назвіть протилежне число. Сусідів числа.
■ II. Перевірка домашнього завдання
Перевіряю наявність Д/з
■ III. Формулювання мети й завдань уроку; мотивація навчальної діяльності
▪ Оголошення теми уроку
▪ Формулювання разом із учнями мети й завдань уроку
▪ Мотивація навчальної діяльності: Сьогоднішній урок є підсумковим з теми «Числові послідовності», у п’ятницю на нас чекає контрольна робота. А не загорами у нас ДПА та ЗНО, на яких також будуть присутні задачі подібні до тих, що ми розвяжемо сьогодні.
■ IV. Актуалізація опорних знань
“ Мозковий штурм.” Запитання до класу:
1.Що утворюють об’єкти ,які пронумеровано натуральними числами? (послідовність)
2.Як називають об’єкти ,які утворюють послідовність? (члени послідовності)
3.Яку послідовність називають числовою? (якщо членами послідовності є числа)
4.Сформулюйте означення арифметичної прогресії. (кожен член якої, починаючи з другого, дорівнює попередньому, до якого додано одне й те саме число)
6.Сформулюйте означення геометричної прогресії. (кожен член якої, починаючи з другого, дорівнює попередньому, помноженому на одне й те саме число)
7.Який вигляд має формула n-го члена арифметичної (геометричної) прогресії?
8.Як пов’язані між собою будь-який член арифметичної (геометричної) прогресії та сусідні з ним члени?
9.Як знайти суму n перших членів арифметичної (геометричної) прогресії ?
■ V. Повторення й аналіз фактів
- В арифметичній прогресії а1=2,1; а10=12,9. Знайти різницю прогресії.
Розв’язання:
![]()
![]()
![]()
![]()
![]()
Відповідь: ![]() .
.
- В геометричній прогресії b1=2,56; b4=4,42368. Обчислити знаменник прогресії.
Розв’язання:
![]()
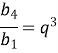
![]()
![]()
![]()
![]()
Відповідь: ![]() .
.
- В арифметичній прогресії а1=20,1; d=1,3. Обчислити суму перших восьми членів прогресії.
Розв’язання:
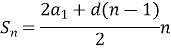
![]()
![]()
Відповідь: ![]() .
.
- В геометричній прогресії b1=1,5; q=1,2. Обчислити суму перших чотирьох членів прогресії.
Розв’язання:
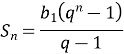
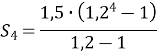
![]()
Відповідь: ![]() .
.
-
Дано прогресію 23,5;
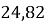 ; 26,14; … знайти сьомий член даної прогресії.
; 26,14; … знайти сьомий член даної прогресії.
Розв’язання:
![]()
![]()
![]()
Отже дана послідовність є арифметичною прогресією.
![]()
![]()
![]()
Відповідь: ![]() .
.
- Дано прогресію 1,5;1,8; 2,16; … Обчислити четвертий член даної прогресії.
Розв’язання:
![]()
![]()
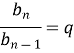
Отже дана послідовність є геометричною прогресією.
![]()
![]()
![]()
Відповідь: ![]() .
.
- Дано прогресію 2,1; 3,3; 4,5; … Обчислити номер члена прогресії, який дорівнює 11,7.
Розв’язання:
![]()
![]()
Отже це є арифметична прогресія, різниця якої d=1,2.
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: Дане число є дев’ятим членом арифметичної прогресії.
- Дано прогресію 1,2; 1,8; 2,7; … Обчислити номер члена прогресії, що дорівнює 4,05.
Розв’язання:
![]()
![]()
Отже ми маємо геометричну прогресію, знаменник якої q=1,5.
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: задане число є четвертим членом геометричної прогресії.
- В арифметичній прогресії а5=14,91; а9=20,11. Обчислити а1.
Розв’язання:
Складемо систему рівнянь і розв’яжемо її.
![]()
![]()
![]()
![]()
![]() .
.
Відповідь: ![]() .
.
- В арифметичній прогресії а7=12,01; а11=17,61. Обчислити різницю прогресії.
Розв’язання:
Складемо систему рівнянь і розв’яжемо її.
![]()
![]()
![]()
Відповідь: ![]() .
.
- В геометричній прогресії b5=64; b8=1. Обчислити b3.
Розв’язання:
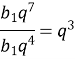
![]()
![]()
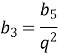
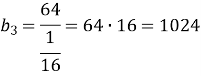
Відповідь: ![]() .
.
- В арифметичній прогресії а9+а15=14,8. Обчислити а12.
Розв’язання:
![]()
![]()
Відповідь: ![]() .
.
-
В геометричній прогресії
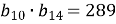 . Обчислити
. Обчислити 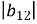 .
.
Розв’язання:
![]()
![]()
Відповідь: ![]() .
.
-
В геометричній прогресії
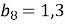 . Обчислити
. Обчислити 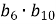 .
.
Розв’язання:
![]()
![]()
Відповідь: ![]() .
.
- Обчислити суму перших п’ятнадцяти непарних чисел.
Розв’язання:
Маємо арифметичну прогресію ![]() .
.
![]()
Відповідь: ![]() .
.
- Обчислити перший член арифметичної прогресії, якщо сума перших дванадцяти членів дорівнює 642, а дванадцятий член дорівнює 48.
Розв’язання:
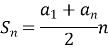
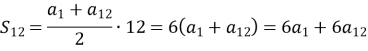
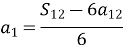
![]()
Відповідь: ![]() .
.
-
Обчислити знаменник геометричної прогресії, яка складається з дійсних чисел, якщо
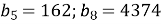 .
.
Розв’язання:
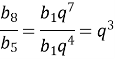
![]()
![]()
Відповідь: ![]() .
.
- В арифметичній прогресії а9=12,4; а23=4,7. Знайти а14+а17.
Розв’язання:
У арифметичній прогресії суми рівновіддалених членів рівні.
![]()
![]()
Відповідь: ![]() .
.
-
В геометричній прогресії
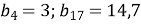 . Обчислити
. Обчислити 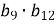 .
.
Розв’язання:
У геометричній прогресії добутки рівновіддалених членів рівні.
![]()
![]()
Відповідь: ![]() .
.
-
Сума п перших членів арифметичної прогресії виражається формулою
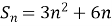 . Знайти а6.
. Знайти а6.
Розв’язання:
Знайдемо ![]() і
і ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: ![]() .
.
-
Сума п перших членів арифметичної прогресії виражається формулою
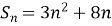 . Знайти різницю прогресії.
. Знайти різницю прогресії.
Розв’язання:
![]()
![]()
![]()
![]()
Відповідь: ![]() .
.
-
В арифметичній прогресії
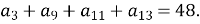 Знайти
Знайти 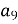 .
.
Розв’язання:
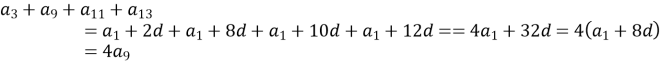
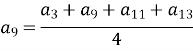
![]()
Відповідь: ![]() .
.
-
В геометричній прогресії
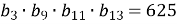 . Обчислити
. Обчислити 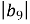 .
.
Розв’язання:
![]()
![]()
![]()
Відповідь: ![]() .
.
-
В арифметичній прогресії
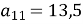 . Обчислити
. Обчислити 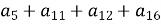 .
.
Розв’язання:
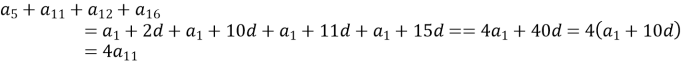
![]()
Відповідь: ![]() .
.
-
В геометричній прогресії
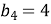 . Обчислити
. Обчислити 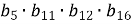 .
.
Розв’язання:
![]() .
.
![]()
Відповідь: ![]() .
.
■ VII. Підбиття підсумків уроку
1.Самостійна робота


2. Бесіда
1. Що ми робили сьогодні на уроці? На які правила виконували завдання?
2. Як ви оцінюєте свою роботу на уроці?
3. Які завдання виявилися найскладнішими? Чому?
4. Що вам необхідно повторити до контрольної роботи.
■ VIII. Домашнє завдання, інструктаж щодо його виконання
Домашня контрольна робота.
І варіант
-
(1 бал) Серед поданих послідовностей укажіть арифметичну прогресію
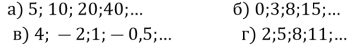
-
(1 бал) Щоб обчислити знаменник геометричної прогресії
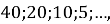 потрібно…
потрібно…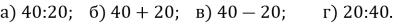
-
(1 бал) Знайдіть суму шести перших членів арифметичної прогресії, якщо її перший член
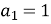 , а різниця
, а різниця 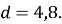

-
(1 бал) П’ятий член арифметичної прогресії, перший член якої
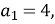 а різниця
а різниця 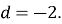

-
(1 бал) Третій член геометричної прогресії , якщо її перший член
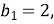 а знаменник
а знаменник 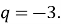

-
(1 бал) Знайдіть суму шести перших членів геометричної прогресії
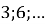 .
.
-
(1 бал) Знайдіть різницю арифметичної прогресії, якщо
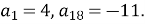
- (1 бал) Між числами 2 і -54 вставте два таких числа, щоб вони разом із поданими числами утворювали геометричну прогресію.
-
(2 бали) Знайдіть суму всіх додатних членів арифметичної прогресії
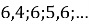 .
.
-
(2 бали) При якому значенні
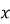 числа
числа 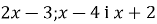 є послідовними членами геометричної прогресії.
є послідовними членами геометричної прогресії.
ІІ варіант
-
(1 бал) Серед поданих послідовностей укажіть геометричну прогресію

-
(1 бал) Щоб обчислити різницю арифметичної прогресії
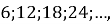 потрібно…
потрібно…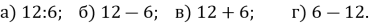
-
(1 бал) Знайдіть суму шести перших членів арифметичної прогресії, якщо її перший член
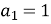 , а різниця
, а різниця 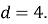

-
(1 бал) Шостий член арифметичної прогресії, перший член якої
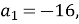 а різниця
а різниця 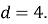

-
(1 бал) Перший член геометричної прогресії , якщо її другий член
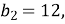 а знаменник
а знаменник 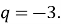

-
(1 бал) Знайдіть суму п’яти перших членів геометричної прогресії
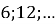 .
.
-
(1 бал) Знайдіть знаменник геометричної прогресії, якщо
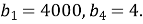
- (1 бал) Між числами 8 і -64 вставте два таких числа, щоб вони разом із поданими числами утворювали геометричну прогресію.
-
(2 бали) Знайдіть суму всіх від’ємних членів арифметичної прогресії
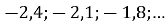 .
.
-
(2 бали) При якому значенні
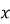 числа
числа 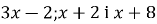 є послідовними членами геометричної прогресії.
є послідовними членами геометричної прогресії.


про публікацію авторської розробки
Додати розробку
