Цікаві логічні завдання з математики для 5-6 класів

Цікаві логічні завдання

1. Перед вами вираз 987654321=100. Зробіть його вірним, використовуючи 4 знаки "+" або "-" у його лівій частині.

Відповідь.  98 - 76 + 54 + 3 + 21 = 100

2. Як відміряти 15 хвилин, маючи під рукою семи- й одинадцяти хвилинні пісочні годинники?

Відповідь. Ставимо одночасно годинники на 7 й 11 хвилин. Як тільки годинник на 7 хвилин повністю пересипався, перевертаємо його. Годинник на 11 ще 4 хвилини пересипається, як тільки він пересипався, перевертаємо заново годинник на 7 хвилин (в якому набігло тільки 4 хвилини), отже, він відміряє ще 4 хвилини, які разом з 11 становлять 15 хвилин.

3.  Скільки в мене квітів, якщо всі з них окрім двох - троянди, всі окрім двох - тюльпани, і всі окрім двох - маргаритки?

Відповідь. 3 (троє квіток)

4. Число із трьох різних цифр віднято із числа, що складається з тих самих цифр, розташованих у зворотному порядку. Результат складається з тих самих трьох цифр, розташованих знову по-іншому. Що це за числа?

Відповідь.   954 - 459 = 495.

5. Два товарних поїзди, обидва довжиною у 250 м, їдуть назустріч один одному з однаковою швидкістю 45 км/год. Скільки секунд пройде після того, як зустрілися машиністи, перш ніж зустрінуться кондуктори останніх вагонів?

Відповідь.  (На товарних поїздах кондукторів не має. Але гіпотетично: :) У момент зустрічі машиністів відстань між кондукторами буде 500 м, тому що кожен поїзд іде зі швидкістю 45+45=90 км/год, або 25 м/сек, шуканий час дорівнює 500:25=20 c.

6. Якщо людина йде на роботу пішки, а назад їде на транспорті, то в цілому на дорогу витрачає півтори години. Якщо ж в обидва кінці він їде на транспорті, то весь шлях займає в нього 30 хвилин. Скільки часу потрібно людині на дорогу, якщо на роботу й назад вона піде пішки?

Відповідь. Користуючись транспортом, людина витрачає на шлях туди й назад 30 хвилин. Тому шлях в одну сторону займає 15 хвилин. Виходить, пішки він може добратися до роботи за 1 годину й 30 хвилин - 15 хвилин = 1 година й 15 хвилин. Весь шлях займе вдвічі більше часу - 2 години й 30 хвилин.

7. Летіла зграя гусей, побачив їх дядько та каже:
   – Мабуть, вас сто!
   А гуси й відповідають:
   – «Якби нас стільки,
   Та ще б стільки,
   Та половину як стільки,
   Та чверть як стільки,
   Та ти б з нами, – тоді б сто й було».
        Скільки гусей?

Відповідь.  36 гусей: 36+36+18+9+1=100.

8.  «Зграя голубів підлетіла до високого дерева. Частина голубів сіла на гілках, а інша розташувалася під деревом. Голуби, що сиділи на гілках, говорять до тих, що внизу: «Якби один з вас злетів до нас, то вас стало б утроє менше, ніж нас всіх разом, а якби один з нас злетів до вас, то нас із вами стало б порівно». Скільки голубів сиділо на гілках і скільки під деревом?

Відповідь. Нехай х − число голубів, що сіли на дерево, а y − число голубів, що розташувалися під деревом. Тоді
y – 1 = (x + y) / 3
і, крім того, х – 1 = y +1, тобто х = y + 2.
     Підставляючи х = y + 2 у перше рівняння, одержуємо
(y – 1) × 3 = y + 2 + y,
3y – 3 = 2y + 2,
y = 5.
     Отже, х = y + 2 = 7.
     Отже, 7 голубів сіли на дерево, а 5 голубів розташувалися під деревом.

9. «Одна жінка відправилася в сад збирати яблука. Щоб вийти із саду, їй потрібно було пройти через четверо дверей, у кожної з яких стояв стражник. Стражникові у перших дверей жінка віддала половину зірваних нею яблук. Дійшовши до другого стражника, жінка віддала йому половину яблук, що залишилися. Так само вона вчинила й з третім стражником; а коли вона поділилася яблуками зі стражником у четвертих дверей (з яким вона вчинили як і з попередніми) то в неї залишилося лише 10 яблук. Скільки яблук вона зібрала в саду?»

Відповідь.  Якщо х - число яблук, зібраних жінкою в саду, то першому стражникові дісталося х /2 яблук, другий одержав х /4 яблук, третій - х/8 яблук і четвертий - х/16 яблук. Так як х/16 = 10, то х = 160. Отже, жінка зібрала в саду 160 яблук.

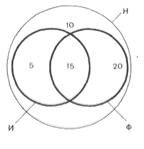
10. Одна швейцарська громада нараховує 50 членів. Рідна мова всіх 50 членів громади − німецька, але 20 з них говорять ще й італійською, 35 з них володіють французькою і 10 не знають ні італійської, ні французької.
         Скільки членів громади говорять і французькою й італійською?

Відповідь. З 50 членів громади 10 говорять тільки на рідній (німецькій) мові. Інші 40 членів громади, крім рідної мови, володіють також французькою або італійською мовою. Так як 20 + 35 = 55, а 55 – 40 = 15, робимо висновок, що 15 членів громади говорять і французькою, й італійською.

11.  Чудовий угорський естрадний обчислювач Ференц Патаки, здатний за лічені секунди подумки перемножити 2 тризначні числа, виступаючи в 1979 р. по телебаченню, продемонстрував наступний фокус.
         «Помножте свій розмір взуття на 2, додайте до добутку 39, помножте отриману суму на 50, додайте до добутку 29, відніміть із суми рік свого народження», − попросив Патаки. На диво глядачів кожний з них одержав чотиризначне число, дві перші цифри якого означають номер взуття, а дві останні − вік глядача наприкінці календарного року.
         Поясніть, на чому заснований фокус Ференца Патаки.

Відповідь.  Для будь-яких натуральних чисел а та b із припустимих множин (розмір черевиків і вік) виконується тотожність:
[(2а+39) • 50+29] − (1979−b) = 100а+b.

12.  Рибу чудово готовлять отут,
         Варена форель − король усіх блюд.
         Замовлення прийняте. Все готово. Несуть!
         По порції риби на стіл подають.
         Але що там за гамір? То кричать кухарі,
         «Для порції нам не вистачає стола,
         І по дві на стіл ми подати б не змогли.
         Залишився б стіл чийсь зовсім без риби».
         Ви назвати б не зуміли
         Нам число порцій форелі
         І кількість столів
         Там, де хвалять кухарів?

Відповідь. Нехай х − число порцій риби, приготованих вправними кухарями, у − число столів. Тоді
у +1= х,
2(у-1)= х,
звідки у +1 = 2(у-1) і у = 3, х = 4.
     Отже, кухарі приготували 4 порції риби, а для гостей було 3 столи.

13.  Проїхавши третину шляху, пасажир швидкого поїзда нарешті заснув. Коли він прокинувся, до станції призначення залишалося проїхати половину тієї відстані, що відокремлювало його від станції призначення, коли він заснув.
         Яку частину шляху проїхав поїзд, поки пасажир спав?

Відповідь.     Так як (1/2) × (2/3) = 1/3, пасажир проспав 1/3 шляху.

14. Звичайно! «Чарівник Думки» ніколи не помиляється. От як це робиться. Попросіть кого-небудь зав'язати вам очі, а потім написати п'ятизначне число, помножити його на дев'ять і закреслити будь-яку цифру. А тепер запропонуйте скласти цифри, що залишилися й назвати суму. Тепер ви легко вгадаєте закреслену цифру. Фантастика!
         Не зрозуміли? Подумайте гарненько.

Відповідь. Бути «Чарівником Думки» насправді просто. Усе, що від вас потрібно, - відняти суму чотирьох чисел (двадцять три) з найближчого до двадцятьом трьом більшого числа, кратного дев'яти. У цьому випадку – це 27. Отже, 27 – 23 = 4. Саме ця цифра й була закреслена. Ця формула підходить у всіх випадках.

15.    Було скількись горобців і скількись стовпців.
         Як сяде по два горобці на один стовпець – буде один лишній стовпець, а як сяде по одному – буде лишній горобець. Скільки було стовпців і горобців?

Відповідь.Три стовпці і чотири горобці.

16.  У мене в двох кишенях є гроші; коли з одної перекладу один карбованець, то буде порівну, а коли з другої перекладу в першу один карбованець, то в першій буде вдвічі більше, ніж в другій. Скільки в кожному кармані карбованців?

Відповідь.      П’ять і сім.

17.   Які три числа, якщо їх додати або перемножити дають той самий результат?

Відповідь.     1, 2, 3.

18.  Написати цифрами число, що складається з 11 тисяч, 11 сотень і 11 одиниць.

Відповідь.      11000 + 1100 + 11 = 12 111

19.   Коли моєму батькові був 31 рік, мені було 8 років, а тепер батько старше мене вдвічі. Скільки мені років тепер?

Відповідь.   23.

20. Моя сестра вдвічі менша за мене. Зараз мені 20 років. Скільки років буде моїй сестрі, коли мені буде 40 років?