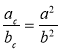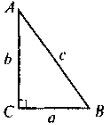ЦИКЛ УРОКІВ ІЗ ГЕОМЕТРІЇ У 8 КЛАСІ З ТЕМИ «ТЕОРЕМА ПІФАГОРА» З ВИКОРИСТАННЯМ ІНТЕРАКТИВНИХ МЕТОДІВ І ПРИЙОМІВ
Перевірити рівень засвоєння учнями змісту основних понять теми та якість сформованих умінь із застосуванням набутих знань, розвивати самостійність, старанність, наполегливість у досягненні мети.
ЦИКЛ УРОКІВ ІЗ ГЕОМЕТРІЇ У 8 КЛАСІ З ТЕМИ «ТЕОРЕМА ПІФАГОРА»
З ВИКОРИСТАННЯМ ІНТЕРАКТИВНИХ МЕТОДІВ І ПРИЙОМІВ
УРОК № 33
Тема: ознаки подібності прямокутних трикутників.
Мета: сформулювати ознаки подібності прямокутних трикутників. Розвивати логічне мислення.
Тип уроку: засвоєння знань та вироблення вмінь.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання. Актуалізація опорних знань учнів.
Усна робота за рисунками до задач, виконаними на дошці заздалегідь. Коло ідей
ІІІ. Формулювання мети і завдань уроку
Нагадую учням про те, що в геометрії виділяють різні види трикутників (за сторонами або кутами). Серед усіх видів трикутників (за кутами) виділяються трикутники, про які можна сказати, що:
- один з кутів завжди дорівнює сумі двох інших;
- вони не можуть бути рівносторонніми, але можуть бути рівнобедреними;
- для того щоб визначити решту кутів цього трикутника, достатньо знати тільки один з його менших кутів. (Зрозуміло, що мова йде про прямокутні трикутники.)
Отже, мета уроку — формулювання ознаки подібності прямокутних трикутника та дослідження сфери її практичного застосування.
IV. Актуалізація опорних знань
З метою успішного засвоєння учнями ознаки подібності прямокутних трикутників, учням слід активізувати такі знання і вміння: ознака подібності трикутників за двома кутами; означення прямокутного трикутника та властивості гострих кутів прямокутного трикутника; застосування поняття про перпендикуляр до прямої, похила та проекція похилої на дану пряму; основні властивості пропорції. Аналіз ситуації
Виконання усних вправ
-
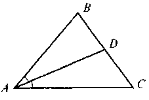
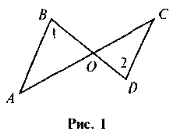
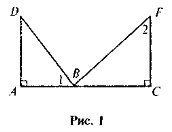
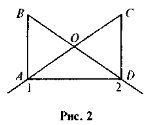
Доведіть, що ΔАВО ~ ΔDCO , якщо
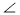 1 =
1 = 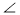 2 (рис. 1).
2 (рис. 1).
-
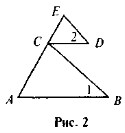
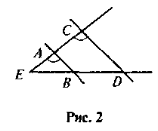
Доведіть, що ΔАВС ~ ΔCDE , якщо AB || CD,
 1 =
1 = 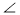 2 (рис. 2).
2 (рис. 2).
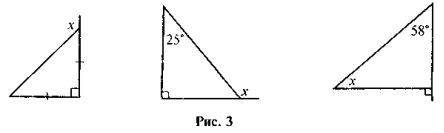
- У кожному з наведених випадків обчисліть міру кута х (рис. 3).
V. Засвоєння знань
План вивчення нового матеріалу
- Ознака подібності прямокутних трикутників (за гострим кутом).
- Ознаки подібності прямокутних трикутників за двома катетами та за гіпотенузою і катетом.
VІ. Формування первинних умінь
- Сформулюйте і доведіть ознаку подібності прямокутних трикутників за двома катетами.
- Сформулюйте і доведіть ознаку подібності прямокутних трикутників за гіпотенузою і катетом.
|
|
||
|
Подібність прямокутних трикутників |
||
|
Ознаки |
||
|
|
|
|
-
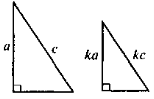
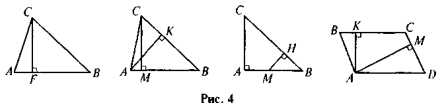
На рис. 4 знайдіть пари подібних трикутників. Свої міркування
обґрунтуйте. Запишіть пропорційність відповідних сторін.
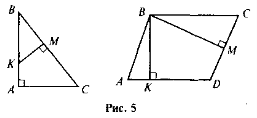
- На рисунку 5 знайдіть подібні трикутники і доведіть їх подібність.
VII. Підсумки уроку
Чи правильні записи зроблені відповідно до рис.5? Якщо ні, виправте помилку.
- АМ + ВМ = АВ;
- ВС2 = МВ · МА.
VIII. Домашнє завдання: розділ 2, вивчити §12, повторити §10, № 537, № 546.
УРОК № 34
Тема: пропорційні відрізки в прямокутному трикутнику.
Мета: сформувати первинні вміння записувати метричні співвідношення між відрізками прямокутного трикутника за умовою задачі, а також виконувати обчислення невідомих відрізків прямокутного трикутника, використовуючи записи відповідних метричних співвідношень, розвивати стійку увагу, культуру математичної мови.
Тип уроку: вироблення вмінь та навичок.
Хід уроку
I. Організаційний момент.
II. Перевірка домашнього завдання
Правильність виконання задач домашньої роботи перевіряю під час усної фронтальної роботи за рисунками до задач, виконаними на дошці заздалегідь.
ІІІ. Формулювання мети і завдань уроку
Використання ознак подібності прямокутних трикутників, дослідження сфери їх практичного застосування.
IV. Актуалізація опорних знань
- Зробіть рисунок, на якому один і той самий відрізок був би одночасно і перпендикуляром, і похилою.
-
Якщо 7а = 9b, то
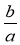 = ? Робота в парах.
= ? Робота в парах.
V. Засвоєння знань
План вивчення нового матеріалу
- Уявлення про зміст поняття середнє пропорційне число між двома числами.
- Теорема (метричні співвідношення в прямокутному трикутнику): формулювання і доведення.
|
Метричні співвідношення |
||
|
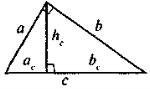
а2 = с · ас, b2 = c · bc,
Наслідки з метричних співвідношень: |
|
|
|
1) |
2) |
|
VІ. Формування навичок та вмінь
Формуванню вмінь записувати та використовувати метричні співвідношення сприятиме виконання усних вправ.
Виконання усних вправ
Запишіть метричні співвідношення для зображених на рис. прямокутних трикутників:
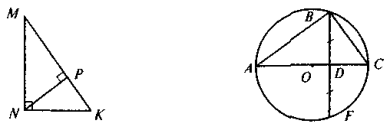
Виконання письмових вправ
-
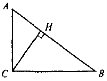
 У прямокутному трикутнику ABC (
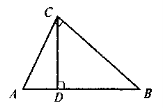
У прямокутному трикутнику ABC (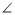 C = 90°) проведено висоту CD (рис.). Знайдіть:
C = 90°) проведено висоту CD (рис.). Знайдіть:
а) CD, якщо AD = 4 см, DB = 25 см;
б) АС і ВС, якщо АВ = 50 см, AD = 18см.
-
Доведіть, що проекції катетів на гіпотенузу прямокутного трикутника відносяться як квадрати катетів:
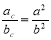 .
.
Мозковий штурм
VII. Підсумки уроку
Чи правильні записи зроблені відповідно до рис.? Якщо ні, виправте помилку
CM = AM · MB; ![]() ; АС2 = АМ · АВ.
; АС2 = АМ · АВ.
VIII. Домашнє завдання: розділ 2, вивчити §12, ІІ частина, №540, №544, №549.
УРОК № 35
Тема: застосування подібності: властивість бісектриси трикутника
Мета: домогтися засвоєння учнями змісту теореми, що виражає властивість бісектриси трикутника та її доведення. Розвивати графічну культуру, творчі здібності учнів.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
За необхідності перевірити виконання письмової частини домашнього завдання, проводжу усну роботу за готовими рисунками до домашніх задач.
III. Формулювання мети і завдань уроку
Нагадую учням, що всі твердження про прямокутний трикутник, які були вивчені протягом останніх двох уроків, ґрунтуються на застосуванні до прямокутного трикутника метричних співвідношень, що випливають із подібності прямокутних трикутників. Отже, мета уроку — вивчення одного з таких співвідношень.
IV. Актуалізація опорних знань
З метою успішного засвоєння учнями змісту навчального матеріалу уроку учням слід активізувати знання і вміння щодо поняття пропорційних відрізків; означення подібних трикутників та ознаки подібності прямокутних трикутників за гострим кутом; означення бісектриси трикутника.
-
Дано:
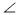 1 =
1 = 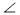 2 (рис. 1). Доведіть, що
2 (рис. 1). Доведіть, що 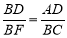 .
.
-
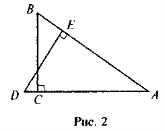
ΔАВС і ΔADE — прямокутні і рівні (рис. 2). Доведіть, що
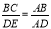 .
.
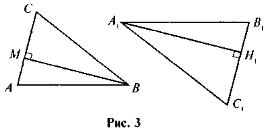
- ΔАВМ ~ ΔВ1А1С1, В, М, А, Н — висоти (рис. 3). Доведіть, що ΔАВМ ~ Δ А1В1Н1.
-
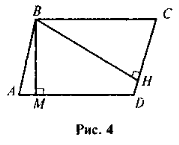
ΔАВМ ~ΔА1ВC, ABCD — паралелограм, ВМ
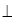 AD, BH
AD, BH 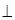 CD (рис. 4). Доведіть, що
CD (рис. 4). Доведіть, що 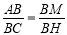 .
.
V. Засвоєння знань План вивчення нового матеріалу
- Теорема про властивість бісектриси трикутника: формулювання і доведення.
- Приклади застосування властивості бісектриси трикутника.
|
|
|
|
Застосування подібності трикутників |
|
|
Властивість бісектриси трикутника
Якщо в ΔАВС: D Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні двом іншим сторонам. |
|
|
|
|
VІ. Формування первинних умінь Виконання усних вправ
- Точки М і Р — середини суміжних сторін AD і DC паралелограма ABCD відповідно. Відрізки МС і РВ перетинаються в точні К . Знайдіть відношення ВК : КР.
- Чи може бісектриса рівнобедреного трикутника ділити бічну сторону у відношенні 2:1, починаючи від основи? Якій теоремі це суперечить?
- Накресліть трикутник ABC і проведіть його бісектрису BD. Виміряйте відрізки АВ , AD і DC . За допомогою властивості бісектриси трикутника обчисліть довжину сторони ВС . Перевірте результат вимірюванням. Робота в групах.
Виконання письмових вправ
- Відрізок BD — бісектриса трикутника ABC. Знайдіть АВ, якщо ВС = 8 см, AD = 3 см, DC = 2 см.
- Відрізок BD — бісектриса трикутника ABC. Знайдіть стороні! трикутника, якщо AD = 8 см, DC = 12 см, а периметр трикутника дорівнює 45 см.
- Бісектриса прямокутного трикутника ділить його катет на відрізки завдовжки 4 см і 5 см. Знайдіть периметр трикутника.
VII. Підсумки уроку
Які помилки допущено в зображенні трикутників?
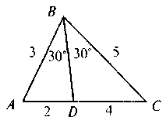
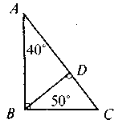
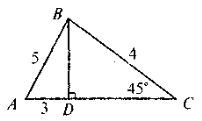
VIII. Домашнє завдання: розділ 2, вивчити §11, теорема 19, №488, №486.
УРОК № 36
Тема: метричні співвідношення в колі. Властивості медіан трикутника.
Мета: домогтися засвоєння учнями змісту теорем про пропорційність відрізків хорд, пропорційність відрізків січної і дотичної та змісту наслідків, властивості медіан. Розвивати пізнавальний інтерес.
Тип уроку: засвоєння нових знань.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Засвоєння змісту матеріалу попереднього уроку та формування оперативних умінь перевіряю під час виконання учнями самостійної роботи.
Самостійна робота із взаємоперевіркою
|
Варіант 1 |
Варіант 2 |
|
1. У трикутнику зі сторонами 25 см і 40 см проведено бісектрису кута між даними сторонами. Вона ділить третю сторону на відрізки, менший з яких дорівнює 15 см. Знайдіть периметр трикутника |
1. У трикутнику ABC найбільша сторона АВ дорівнює 40 см. Бісектриса BD ділить сторону АС на відрізки завдовжки 15 см і 24 см. Знайдіть периметр трикутника ABC |
|
2. Бісектриса прямого кута прямокутного трикутника ділить гіпотенузу на відрізки завдовжки 15 см і 20 см. Знайдіть довжини відрізків гіпотенузи, на які її ділить висота трикутника |
2. Висота прямокутного трикутника ділить гіпотенузу на відрізки 12,6 см і 22,4 см. Знайдіть довжини відрізків гіпотенузи, на які її ділить бісектриса прямого кута |
III. Формулювання мети і завдань уроку
Мета уроку — вивчення інших, ніж на попередньому уроці, співвідношень.
IV. Актуалізація опорних знань
З метою свідомого засвоєння учнями змісту теорем та їх доведення учням слід активізувати знання і вміння щодо знання означень та властивостей хорд, дотичних та січних; означення вписаного кута та властивості вимірювання вписаного кута і наслідку з неї; ознак подібності трикутників.
Виконання усних вправ Синтез думок
-
Дайте назви всім відрізкам (рис. 1). Яка точка кола на рисунку 1 (б)
найближча до точки А? Найвіддаленіша від точки А?
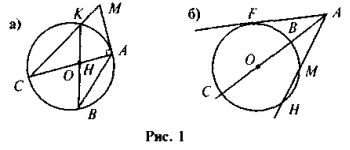
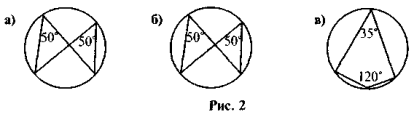
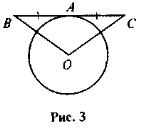
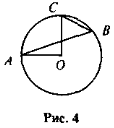
- Чи все правильно нарис. 2?
- ВС — дотична, О — центр кола, АВ = АС (рис. 3). Доведіть, що ОВ = ОС.
-
О — центр кола,
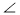 АВС = 45° (рис. 4). Знайдіть кут АОС.
АВС = 45° (рис. 4). Знайдіть кут АОС.
V. Засвоєння знань План вивчення нового матеріалу
- Пропорційність відрізків хорд.
- Пропорційність відрізків січної та дотичної.
- Пропорційність відрізків січних.
- Властивість медіан.
VI. Формування первинних умінь Виконання усних вправ
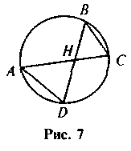
- Знайдіть (рис. 7):
1) АН і ВС, якщо DM = 4, НВ = 5, НС = 10, AD = 3;
2) AC, AD : ВС, якщо АН : НС = 3 : 2, DH = 4, НВ = 6.
-
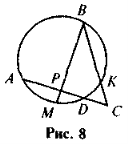
Знайдіть (рис. 8): 1) АР, якщо АР = DP, AC
 BP, АС = 12, СК = 4, ВК= 6;
BP, АС = 12, СК = 4, ВК= 6;
2) радіус кола, якщо AD ![]() ВК , АР = DP, BP = 4PM, DC = 2, СК = 1, ВС = 20.
ВК , АР = DP, BP = 4PM, DC = 2, СК = 1, ВС = 20.
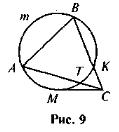
-
МС - дотична, МС = 6, АС = СВ, СК = 3, АВ = 12 (рис. 9). Знайдіть
 ABC.
ABC.
Виконання письмових вправ Розумовий штурм
- При перетині з діаметром кола, хорда ділиться на відрізки завдовжки 3 см і 4 см, а діаметр — у відношенні 1 : 3. Знайдіть радіус кола.
- Із точки поза колом, віддаленої від найближчої точки кола на 24 см, проведено дотичну до кола. Знайдіть радіус кола, якщо відрізок дотичної дорівнює 36 см.
- Хорда перпендикулярна до діаметра. Відстані від одного з кінців хорди до кінців діаметрів дорівнюють відповідно 10 см і 24 см. Обчисліть довжини хорди і діаметра.
VIІ. Підсумки уроку
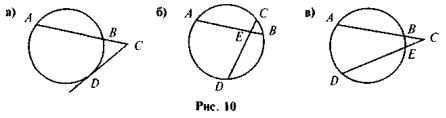
До кожного з наведених рисунків виберіть відповідну рівність. Поясніть свій вибір.
1) АЕ · BE = СЕ · DE; 2) АС · ВС = CD · СЕ; 3) AC · BC = CD2.
VIIІ. Домашнє завдання: розділ 2, вивчити §11, повторити §10, №503, №508.
УРОК № 37
Тема: теорема Піфагора
Мета: сформувати в учнів розуміння змісту теореми Піфагора та її доведення. Формувати вміння відтворювати зміст теореми Піфагора, застосовувати її для розв'язування задач на знаходження невідомих сторін прямокутних трикутників. Розвивати пізнавальний інтерес, стійкі обчислювальні навички.
Типу уроку: засвоєння нових знань.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Під час усного обговорення контрольних моментів розв'язання домашніх задач учні мають відтворити аргументовані міркування із використанням ознак подібності прямокутних трикутників та метричних співвідношень у прямокутному трикутнику. Чи справді це так?
III. Формулювання мети і завдань уроку
Завдання на урок формулюється так: спираючись на відомі учням співвідношення в прямокутному трикутнику, сформулювати твердження, що виражає залежність між сторонами прямокутного трикутника, довести його. А також сформувати вміння застосовувати ці залежності для знаходження невідомих сторін прямокутного трикутника.
IV. Актуалізація опорних знань Виконання усних вправ за готовими рисунками
|
1 |
|
1) АС2, СН, якщо АН = 2, ВН = 8;2) АН, якщо ВС = 6, НВ = 4; 3) СН, якщо АС = 3, ВС = 4;4) АВ, якщо ВС = 10, СН = 6 |
|
2 |
|
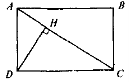
DH 1) РАBCD, якщо АН = 9, СН = 16; 2) DH, якщо АВ = 12, AD = 5; 3) АС, якщо AD = 15, DH = 12; 4) РABCD, якщо AD + DC = 70, AH · HC = 9 · 16 |
V. Засвоєння знань План вивчення нового матеріалу
- Теорема Піфагора: доведення та формулювання. Приклади застосування
|
Теорема Піфагора. Обернена теорема до теореми Піфагора
Теорема Піфагора. Якщо в ΔВС АВ2 = АС2 + ВС2 (с2 = а2 + b2). |
|
VI. Формування первинних умінь
Виконання усних вправ Робота в парах
- У ромбі відомі сторона та одна з діагоналей. Як знайти іншу діагональ ромба, не користуючись рисунком?
- 1) Катети прямокутного трикутника 5 см і 12 см. Знайдіть гіпотенузу.
2) Гіпотенуза трикутника 5 см, а один із катетів дорівнює 3 см. Знайдіть другий катет.
3) Катети прямокутного трикутника відносяться як 3 . 4, а гіпотенуза дорівнює 15 см. Знайдіть периметр трикутника.
4) Периметр квадрата дорівнює 4 см. Знайдіть діагональ квадрата.
5) Визначте вид трикутника ABC, якщо: 1) АС = 5, ВС = 6 , АС = 7; 2) АС = 4. ВС = 2![]() , AC = 6.
, AC = 6.
Виконання графічних вправ
Накресліть прямокутний трикутник із катетами 3 см і 4 см. Обчисліть за теоремою Піфагора довжину його гіпотенузи. Перевірте результат вимірюванням.
Виконання письмових вправ
- У прямокутному трикутнику з катетами а і b та гіпотенузою с знайдіть с, якщо а = 7, b = 24 .
- У прямокутнику знайдіть периметр, якщо діагональ дорівнює 10 см, а одна зі сторін — 6 см.
- Основа рівнобедреного трикутника дорівнює 16 см. Знайдіть периметр трикутника, якщо його бісектриса, проведена до основи, дорівнює 6 см.
VII. Підсумки уроку
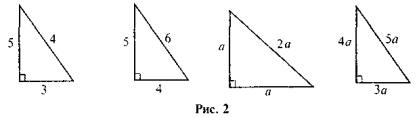
На якому з рисунків (див. рис. 2) допущені помилки в зображенні прямокутного трикутника?
VIII. Домашнє завдання: розділ 2, вивчити §13, теорема 25, №573, №575, №583.
УРОК № 38
Тема: теорема, обернена до теореми Піфагора
Мета: домогтися свідомого розуміння учнями змісту теореми Піфагора та її доведення: сформувати поняття єгипетського трикутника, піфагорової трійки чисел, піфагорових трикутників. Формувати вміння відтворювати зміст вивченої теореми та застосовувати її під час розв'язування задач на доведення. Розвивати логічне мислення, кмітливість, допитливість.
Тип уроку: засвоєння нових знань, вироблення вмінь та навичок.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Засвоєння учнями змісту теореми Піфагора та первинних умінь її використання перевіряю, провівши математичний диктант.
Математичний диктант
|
|
Варіант 1 |
Варіант 2 |
|
1 |
Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють відповідно 5 м і 12 м |
Знайдіть катет прямокутного трикутника, якщо його інший катет і гіпотенуза дорівнюють відповідно 40 см і 41 см |
|
2 |
Запишіть теорему Піфагора для ΔАВС , у якому |
|
|
|
|
|
|
3 |
Знайдіть катет прямокутного трикутника, якщо інший катет і гіпотенуза дорівнюють відповідно 60 дм і 61 дм |
Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють відповідно 6 мм і 8 мм |
|
4 |
Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює 6,5 см. Знайдіть трикутники, якщо один із катетів має довжину 5 см |
Знайдіть радіус кола, описаного навколо прямокутного трикутника з катетами 8 дм і 15 дм |
III. Формулювання мети і завдань уроку Гра «Що? Де? Коли?» Питання знавцям
Давні єгиптяни будували прямі кути на місцевості таким чином: ділили вузлами мотузку на 12 рівних частин, зв'язували її кінці, після чого мотузку розтягувати на землі так, щоб утворився трикутник зі сторонами 3, 4 і 5 поділок. Кут трикутника, що лежав проти сторони з 5-ма поділками, був прямий. Чи можете ви обґрунтувати правильність цієї побудови або спростувати її?
Таким чином формулюється загальна проблема: як, не проводячи вимірювань, визначити, чи є трикутник із заданими довжинами (співвідношенням) сторін прямокутним, розв'язання якої і є основною метою уроку.
IV. Актуалізація опорних знань
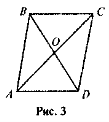
-
Дано:
 M =
M = 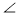 B = 90°, МС = ВС (рис. 1). Доведіть, що АВ = МН.
B = 90°, МС = ВС (рис. 1). Доведіть, що АВ = МН.
-
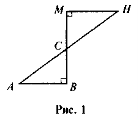
Дано: AB
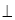 AD, CD
AD, CD 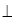 AD,
AD,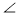 1 =
1 = 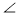 2 (рис.2).Доведіть, що ΔABD = ΔDCA.
2 (рис.2).Доведіть, що ΔABD = ΔDCA.
- Диктант.
- Якщо катети прямокутного трикутника дорівнюють 12 см і 9 см, то гіпотенуза дорівнює...
- Якщо дві більші сторони прямокутного трикутника дорівнюють 17 і 15, то третя сторона дорівнює...
- Якщо діагональ квадрата дорівнює 12 см, то сторона квадрата має довжину...
- Якщо діагоналі ромба мають довжини 12 см і 16 см, то сторона ромба має довжину.
V. Засвоєння знань План вивчення нового матеріалу
- Теорема, обернена до теореми Піфагора: формулювання та доведення. Єгипетський трикутник.
- Піфагорові трійки чисел, піфагорові трикутники. Реферати, підготовлені учнями.
VI. Формування первинних умінь Виконання письмових вправ
-
Визначте, чи є прямокутним трикутник зі сторонами: а) 4, 5, 6; б) 2,
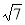 ,
, 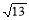 .
.
- Діагоналі паралелограма дорівнюють 16 см і 30 см, а сторона – 17 см. Доведіть, що даний паралелограм є ромбом.
- Сторони трикутника дорівнюють 15 см, 20 см і 25 см. Знайдіть медіану і висоту, проведену до найбільшої сторони.
- У рівнобедреному прямокутному трикутнику знайдіть:
а) гіпотенузу, якщо катет дорівнює 4 см; 2![]() см; а см;
см; а см;
б) катет, якщо гіпотенуза дорівнює 10 см; ![]() см; с см.
см; с см.
VII. Підсумки уроку
Дві сторони трикутника мають довжини 4 см і 5 см. Якою може бути довжина третьої сторони, щоб цей трикутник був прямокутним? Піфагоровим?
VIII.Домашнє завдання: розділ 2, повторити §13, №605, №609, №615.
УРОК № 39
Тема: перпендикуляр і похила. Розв'язування задач
Мета: сформувати в учнів свідоме розуміння змісту понять похилої до прямої, проекції похилої на пряму, а також властивостей перпендикуляра, похилих та їх проекцій. Розвивати графічну культуру, навички самостійного мислення.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
І. Організаційний етап
II. Перевірка домашнього завдання Математичний диктант Незакінчене речення
|
|
Варіант 1 |
Варіант 2 |
|
1 |
Закінчіть речення: Якщо квадрат сторони трикутника дорівнює сумі квадратів двох його інших сторін, то... |
У ΔMNK MN2 = МК2 + NK2. Знайдіть градусну міру найбільшого кута ΔММК |
|
2 |
У ΔSTO ST2 + ТО2 = SO2. Яка градусна міра найбільшого кута ΔSTO? |
Заповніть пропуски: Якщо квадрат сторони... дорівнює сумі квадратів двох інших сторін..., то кут... прямий |
|
3 |
Визначте, чи є в трикутнику прямий кут, якщо його сторони |
|
|
|
40 см, 41 см, 9 cm |
25 см, 24 см, 27 см |
|
4 |
Діагоналі паралелограма мають довжину 6 см і 8 см, а одна зі сторін — 5 см. Що можна сказати про цей паралелограм? |
Відомо, що довжина сторін паралелограма 5 см і 12 см, а одна з діагоналей має довжину 13 см. Що можна сказати про цей паралелограм? |
III. Формулювання мети і завдань уроку
Повідомляю про те, що в математиці існують поняття, властивості яких мають пряме відношення до теореми Піфагора. На уроці відбудеться ознайомлення учнів з цими поняттями, а також будуть досліджені їх властивості, що випливають із тверджень теореми Піфагора.
 IV. Актуалізація опорних знань Виконання усних вправ Вирішення проблем
IV. Актуалізація опорних знань Виконання усних вправ Вирішення проблем
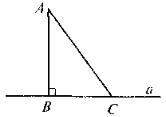
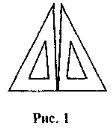
- Два креслярські трикутники розміщені так. як показано на рис. 1. Що можна сказати з цього приводу?
- Чи може діагональ прямокутника бути меншою за одну з його сторін?
-
Чи може діагональ ромба бути в два рази
довшою за його сторону? - У теоремі Піфагора назвіть умову і висновок.
Засвоєння знань План вивчення нового матеріалу
- Похила, проведена з точки до прямої; основа перпендикуляра та основа похилої; проекція похилої на пряму.
- Властивості перпендикуляра, похилих та їх проекцій.
|
Перпендикуляр і похила |
||
|
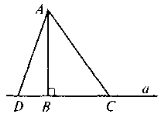
Відрізок АВ — перпендикуляр до прямої а; відрізок АС — похила до прямої; відрізок ВС — проекція похилої АС на пряму а . |
||
|
|
||
|
Властивості
Якщо АВ 1) АС > АВ; АС > ВС;
2) АС = AD
3) AC > AD |
|
|
|
Якщо перпендикуляр і похила проведені з однієї точки до однієї прямої, то |
||
|
будь-яка похила більша за перпендикуляр і за свою проекцію |
Рівні похилі мають рівні проекції, і навпаки |
більша похила має більшу проекцію, і навпаки |
VI. Формування первинних умінь Виконання усних вправ
- Із точки поза прямою проведено до неї дві похилі, одна з яких має довжину 10 см і утворює зі своєю проекцією на пряму кут 30°. Знайдіть довжину другої похилої, якщо вона утворює з прямою кут 45°.
-
У трикутнику ABC
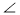 1 = 90°. Назвіть:
1 = 90°. Назвіть:
а) похилу до прямої АВ , проведену з точки С; б) проекцію похилої ВС на пряму АС .
Виконання письмових вправ
- Із точки, взятої на відстані 12 см від прямої, проведено до неї дві похилі. Знайдіть відстань між основами похилих, якщо їх сума дорівнює 28 см, а проекції похилих відносяться як 5 : 9.
- Із однієї точки до даної прямої проведено дві рівні похилі. Відстань між їх основами 14 см. Визначте проекції похилих на дану пряму.
VII. Підсумки уроку. Проаналізувати вивчений теоретичний матеріал.
VIII. Домашнє завдання: розділ 2, вивчити §14, № 633, №637, №643.
УРОК № 40
Тема: розв'язування задач
Мета: узагальнити та систематизувати знання учнів про
зміст та схеми застосування теорем, що випливають із подібності трикутників (властивості бісектриси трикутника та метричних співвідношень у колі); удосконалювати вміння та навички застосування набутих знань, розвивати логічне мислення.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Засвоєння учнями матеріалу попереднього уроку (метричні співвідношення в колі) проводжу у формі «німого» диктанту. На дошці виконане зображення ситуацій, що можуть бути описані метричними співвідношеннями в колі (рис. 1).
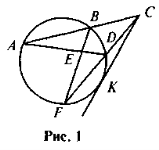
Формулюю загальне завдання для всіх учнів: для відрізків, на які вказую, записати правильну рівність (відповідне метричне співвідношення). 1 далі мовчки вказую по черзі на відрізки хорд, січних, дотичних. По закінченні виконання роботи відбувається взаємоперевірка робіт із коментарем.
III. Формулювання мети і завдань уроку
Якість виконання роботи на попередньому етапі уроку дає можливість сформулювати мету уроку або як закріплення знань, набутих під час вивчення застосування подібності трикутників та продовження роботи із формування навичок практичного застосування знань, або ж як відпрацювання навичок застосування знань та вдосконалення вмінь.
IV. Закріплення знань учнів
Повторення та систематизація знань учнів про зміст тверджень, які випливають із подібності трикутників, проводжу в такій формі: до уваги учнів пропонується рис. 2, за яким вони виконують завдання: для кожного з рисунків скласти найбільш відповідне твердження (у математичному та словесному вигляді). Для того щоб залучити до роботи якомога більше учнів, можна організувати роботу в малих групах. У такому разі спочатку завдання виконується в групах, а потім результати презентуються та в разі необхідності коригуються.
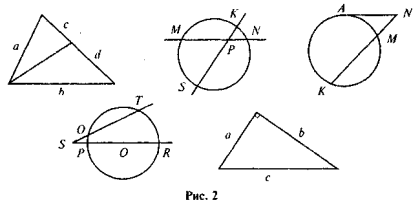
V. Удосконалення вмінь
Застосування знань у стандартних ситуаціях
- Бісектриса кута при основі рівнобедреного трикутника ділить висоту, проведену до основи, на відрізки завдовжки 16,5 см і 27,5 см. Знайдіть відрізки, на які ця бісектриса ділить бічну сторону трикутника.
- Відрізок ВР є бісектрисою трикутника ABC. Знайдіть:
а) АВ. якщо ВС = 9 см, АР = 7,5 см, PC = 4,5 см;
б) PC, якщо АВ = 30 см, АР = 20 см, ВР = 16 см і ![]() BPC =
BPC = ![]() C;
C;
в) РС, якщо АВ = 14 см, ВС = 20 см, АС = 21 см.
- Хорди АВ і СК перетинаються в точці Р. Знайдіть довжини хорд, якщо відомо, що:
1) АР = 8 см, ВР = 12 см і СК : РК = 3 : 8;
2) АР : РВ = 16 : 1, СК – СР = 9 см і АВ + СК = 76 см. Синтез думок.
Застосування знань у нестандартній ситуації
- Катет прямокутного трикутника дорівнює 28 см. Точка, що належить гіпотенузі, віддалена від кожного з катетів на 12 см. Знайдіть довжини відрізків, на які ця точка ділить гіпотенузу.
- У трикутник MNK вписано ромб MDEF так, що вершини D, Е і F лежать відповідно на сторонах MN, NK і МК. Знайдіть відрізки NE і ЕК, якщо MN = 7 см, NK = 6 см, МК = 5 см.
Мозковий штурм
VI. Підсумки уроку
Закінчивши розв'язання задач, учні здійснюють самооцінку знань і вмінь та усвідомлюють, над якими питаннями теми слід додатково працювати.
VIІ. Домашнє завдання: розділ 2, повторити §§10-14, задачі за готовими малюнками, стор.134, №1-4 (А).
УРОК № 41
Тема: підсумковий урок. Самостійна робота.
Мета: повторити, систематизувати та узагальнити набуті
знання під час вивчення теми «Подібність трикутників. Теорема Піфагора». Вдосконалити вміння учнів щодо застосування вивчених теоретичних тверджень під час розв'язування типових задач. Розвивати стійку увагу, навички самоконтролю.
Тип уроку: узагальнення та систематизація знань, умінь і навичок.
Хід уроку
І. Організаційний етап
ІІ. Перевірка домашнього завдання. Самостійна робота.
Збираю зошити із виконаними задачами на застосування подібності та із самостійною роботою. Потім проводжу перевірку виконання самостійної роботи та корекцію; до уваги учнів пропонується правильне розв'язання задач самостійної роботи, записане на ІАК дошці заздалегідь.
-
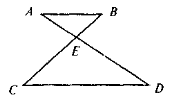 Доведіть подібність трикутників ABE і DCE. якщо АВ || CD (рис. ).
Доведіть подібність трикутників ABE і DCE. якщо АВ || CD (рис. ).
- Периметр прямокутника дорівнює 34 см, а одна зі сторін — 5 см. Знайдіть діагональ прямокутника.
- Сторони трикутника пропорційні числам 21, 20 і 29. Доведіть, що даний три кутник прямокутний.
- Із точки до прямої проведено перпендикуляр і дві похилі завдовжки 17 см і 10 см. Проекції похилих відносяться як 2 : 5. Знайдіть довжину перпендикуляра.
- У прямокутному трикутнику бісектриса ділить гіпотенузу на відрізки 15 см і 20 см. На які відрізки ділить гіпотенузу висота трикутника? Взаємоперевірка
III. Формулювання мети і завдань уроку
Основна дидактична мета та завдання на урок цілком логічно випливають із місця уроку в темі. Оскільки урок є останнім, підсумковим, то головну увагу приділяю питанню повторення, узагальнення та систематизації знань та вмінь, набутих учнями в ході вивчення теми «Подібність трикутників. Теорема Піфагора». Таке формулювання мети створює відповідну мотивацію діяльності учнів.
IV. Повторення та систематизація знань
Організовую роботу учнів в ігровій формі «Закінчити речення», або ж провести «Інтелектуальний аукціон», проводжу традиційне опитування (у формі інтерактивної вправи «Мікрофон») за основними питаннями теми. Список питань відповідає списку контрольних запитань до розділу II (див. підручник).
V. Систематизація вмінь
Застосування знань учнів у стандартних ситуаціях
Учні усно розв'язують завдання (або відтворюють план розв'язання типових задач) за готовими рисунками.
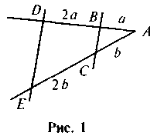
- За даними рис. 1 доведіть, що ΔАВС ~ ΔADE.
-
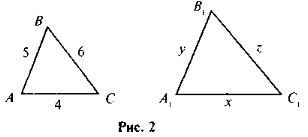
На рис. 2 ΔАВС ~ ΔА1В1С1,
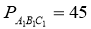 . Знайдіть х, у і z.
. Знайдіть х, у і z.
-
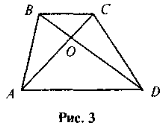 На рис. З ABCD — трапеція. Доведіть, що ΔВОС ~ ΔDOA .
На рис. З ABCD — трапеція. Доведіть, що ΔВОС ~ ΔDOA .
Застосування знань учнів у нестандартних ситуаціях
- Знайдіть сторони рівнобедреного трикутника з периметром 16 см, якщо медіана, проведена до основи, дорівнює 4 см.
- Периметр рівнобедреної трапеції дорівнює 1 м, а різниця основ складає 14 см. Знайдіть радіус кола, вписаного в трапецію.
- Катет прямокутного трикутника дорівнює 32 см. Точка, що лежить на цьому катеті, віддалена від кінців гіпотенузи на 25 см. Знайдіть периметр трикутника.
- Прямокутний трикутник із катетами а і b та гіпотенузою с подібний прямокутному трикутнику з катетами а1 і b1 та гіпотенузою с1/ Доведіть, що аа1 + bb1 = сс1.
VI. Підсумки уроку
Основним підсумком уроку має бути усвідомлення учнями низки задач, які вони мають уміти розв'язувати із використанням знань, набутих під час вивчення теми 3.
VII. Домашнє завдання: розділ 2, повторити §§ 8-14, №1-7 (І група), №5-10 (ІІ група), типові завдання для сам ост. Роботи, стор.137.
УРОК № 42
Тема: контрольна робота з теми «Теорема Піфагора» (№ 5)
Мета: перевірити рівень засвоєння учнями змісту основних
понять теми та якість сформованих умінь із застосуванням набутих знань, розвивати самостійність, старанність, наполегливість у досягненні мети.
Тип уроку: контроль та корекція знань.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Збираю зошити із виконаною домашньою контрольною роботою (роботу перевіряю та враховую під час виставлення тематичного бала).
ІІІ. Формулювання мети і завдань уроку
 Ще раз наголошую, що метою контрольної роботи є демонстрація учнями своїх навчальних досягнень, а саме: показати знання змісту основних понять, вивчених у темі, а також оволодіння способами дій із застосування набутих знань під час розв'язування задач.
Ще раз наголошую, що метою контрольної роботи є демонстрація учнями своїх навчальних досягнень, а саме: показати знання змісту основних понять, вивчених у темі, а також оволодіння способами дій із застосування набутих знань під час розв'язування задач.
IV. Умова контрольної роботи № 5
Варіант І
- Сторони трикутника пропорційні числам 21, 20 і 29. Доведіть, що даний три кутник прямокутний.
- Із точки до прямої проведено перпендикуляр і дві похилі завдовжки 17 см і 10 см. Проекції похилих відносяться як 2 : 5. Знайдіть довжину перпендикуляра.
- Із точки до прямої проведено дві похилі. Довжина однієї з них дорівнює 45 см, а довжина її проекції на пряму — 21 см. Знайдіть довжину другої похилої, якщо вона утворює з прямою кут 45°.
- Основи прямокутної трапеції дорівнюють 14 см і 24 см. а більша діагональ є бісектрисою прямого кута. Знайдіть периметр трапеції.
 Варіант 2
Варіант 2
- Сторони трикутника пропорційні числам 6, 10 і 8. Доведіть, що даний три кутник прямокутний.
- Із точки до прямої проведено перпендикуляр і дві похилі завдовжки 24 см і 20 см. Проекції похилих відносяться як 2 : 5. Знайдіть довжину перпендикуляра.
-
Із точки до прямої проведено дві похилі. Одна з них завдовжки 24
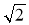 см утворює з прямою кут 45°. Знайдіть довжину другої похилої, якщо її проекція на пряму дорівнює 18 см.
см утворює з прямою кут 45°. Знайдіть довжину другої похилої, якщо її проекція на пряму дорівнює 18 см.
- Основи прямокутної трапеції дорівнюють 24 см і 34 см, а менша діагональ є бісектрисою прямого кута. Знайдіть периметр трапеції.
VII. Підсумки уроку
VIII. Домашнє завдання Виконати аналіз контрольної роботи


про публікацію авторської розробки
Додати розробку