Цикл уроків у 6 класі за темою: «Відношення та пропорції»

В

Відділ освіти

Пирятинської райдержадміністрації

Районний методичний кабінет

 

Цикл уроків у 6 класі

за темою:

«Відношення та пропорції». 

 

 

     Підготувала

                   вчитель математики

Великокручанської зш І-ІІІ ст.

                                    Леонова Л.М.

 

 

 

     В даній розробці пропонується цикл уроків для 6 класу з теми «Відношення та пропорції».

     Підібрано ряд задач практичного змісту, про світ живої природи, використано місцевий матеріал. Це сприятиме підсиленню практичної спрямованості шкільного курсу математики і внесе різноманітність та емоційне забарвлення в навчальний процес.

 

 

    Збірник може бути використаний вчителями математики загальноосвітніх шкіл.

 

 

 

 

 

 

 

 

 

Урок №1

 

 

 

 

 

Мета уроку: узагальнити знання учнів про

                               зміст дії ділення чисел;

                               сформувати уяву про поняття                     

                               відношення двох чисел, його

                               змісту та основної властивості

                               відношення;

                               виховувати культуру

                               математичної мови;

                               розвивати логічне мислення

                               учнів;

                               показати практичне              

                               застосування математики;

                               виховувати любов до природи

                               та до праці.

 

Тип уроку:   засвоєння нових знань.

 

 

Хід уроку

 

І.    Актуалізація опорних знань.

   

   1.   Повторюємо дії додавання, віднімання, множення, ділення, піднесення до степеня. Акцентуємо при цьому увагу на дії ділення.

   2.    Повторюємо основну властивість частки.

   3.    Усні вправи:

а)    200 : 40;                              3,8 : 1,9;                                     

б)    скоротіть дріб:

      

в)    у скільки разів 90 більше за 30; 30 менше за 90; 90 більше за 60; 60 менше за 90; а більше від в; в менше від а?

г)    яку частину становить30 від 90; а від в?

 

ІІ.    Мотивація навчальної діяльності.

 

  Розглянемо задачу:

  Учні шостих класів нашої школи під час суботника посадили 90 молодих саджанців дерев. Учні 6-А класу посадили 50 дерев. Яку частину всіх дерев посадили учні 6-А класу? У скільки разів більше посадили дерев учні 6-А класу, ніж учні 6-Б класу?

                                                (   у 1,25 рази )

  При розв’язуванні таких та інших задач, а також у повсякденному житті нам доводиться мати справу з питаннями двох видів:

1. у скільки разів одна величина більша за іншу або друга менша від першої?
2. яку частину становить одна величина від іншої?

  Щоб дати відповіді на поставлені запитання нам потрібно виконати ділення одного числа на інше: або більше з чисел ділимо на менше, або менше ділимо на більше. Саме про такі частки ми і поговоримо більш докладно на сьогоднішньому уроці.

 

ІІІ.    Вивчення нового матеріалу.

 

1.      Означення        ( ст. 106 підручника)

а : в – відношення а до в.

         Наприклад:     

50 : 90 – відношення 50 до 90 ( менше 1 );

90 : 50 – відношення 90 до 50 ( більше 1 ).

 

2.     Відношення показує:

    а)  яку частину становить а від в, якщо а ‹ в;

    б)  у скільки разів а більше за в, якщо а › в.

       

          Наприклад:

а)    50 : 90 показує, що 50 становить від 90   частину;

б)    90 : 50 показує, що 90 більше від 50 у 1,25 рази.

 

3.    Основна властивість відношення                    ( ст. 107 підручника):

                                     або                 

          Наприклад:

      

  Зауваження:  на основі цієї властивості зручно заміняти відношення дробових чисел на відношення натуральних чисел.

         Наприклад:

1,2 : 2,3 = 12 : 23.

Фізкультхвилинка

 

Математична хвилинка

 

  Як розділити 4 яблука, що лежать у корзині, між 4 дітьми так, щоб одне яблуко залишилося у корзині?

               (Одній дитині дати яблуко з корзиною)

 

Екологічна хвилинка

 

  На території України налічується близько 10 тис. видів грибів, але збирають лише 10 видів. У скільки разів і на скільки більше відомо видів грибів, ніж їх збирають?

                               ( У 1000 разів; на 9 900 видів )

 

4. Формування вмінь і навичок.

 

  Усні вправи № 607, 608

 

  Знайти відношення № 609, 610

 

 

  Спростити відношення № 616

 

  Замінити відношення дробових чисел відношенням натуральних чисел

 № 618 

 

  Розв’язати задачі № 612, 615, 620, 622, 624, 625, 626

            № 612

1. 48 : 36 = 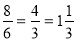( рази )
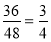2. ( частину )

  Зауваження до № 612:    

  - обернені відношення.

          № 624  ( хто швидше )

1. 1,5 + 0,75 = 2,25 ( м² ) – пофарбував Бен;
2. 2,25 : 1,5 = 1,5 ( рази ) – більше пофарбував Бен.

 

№ 628   ( змагання між рядами )

1. 540 : 0,3 = 1 800 ( коп. ) = 18 ( грн.) – коштує 1 кг сиру;
2. 400 : 0,25 = 1 600 ( коп.) = 16 ( грн.) – коштує 1 кг бринзи;
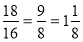3. ( рази ) – дорожчий кілограм сиру.

 

5. Підсумок уроку.

   

    Повторюємо основні поняття, вивчені на уроці і звертаємо увагу на те, де і як саме їх можна використати.

    Наголошуємо на ті вправи, які викликали труднощі при розв’язанні.

    Оцінюємо разом з учнями роботу окремих школярів.

 

 

 

6. Домашнє завдання.

 

   1.   Прочитати п.20 підручника та вивчити означення відношення двох чисел і основну властивість відношення.

    2.  Виконати : № 611, 613, 617, 619, 621 /

    3.  Додаткове завдання:   № 628.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Урок №2

 

 

 

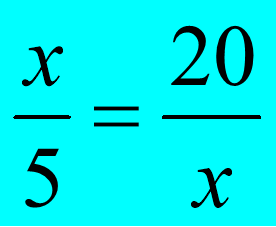
Мета уроку: сформувати уявлення учнів про

                                 зміст понять  пропорція, члени 

                                 пропорції, основна властивість

                                 пропорції та виробити вміння  

                                 застосовувати ці поняття під

                                 час розв’язування типових

                                 завдань;

                                 розвивати навички усного 

                                 рахунку;            

                                 показати учням загально-               

                                 інтелектуальне значення 

                                 математики;

                       розвивати в учнів творчу та

                                 пізнавальну активність;

                                 розвивати інтерес до

                                 математики.

Тип уроку:     засвоєння нових знань.

 

Хід уроку

 

І.    Актуалізація опорних знань.

 

    1.  Робота в парах ( учні повторюють означення відношення та основну властивість відношення).

    2.  Мікрофон ( декілька учнів озвучують ці правила в мікрофон ).

    3.  Усні вправи:

а)  чому дорівнює відношення чисел 20 і 4; 15 і 3?

б)  відношення якого числа до числа 8 дорівнює 4?

в)  відношення числа 56 до числа а дорівнює 7. чому дорівнює число а?

г)  скоротіть відношення 5 хв до 1 год.

 

ІІ.    Мотивація навчальної діяльності.

 

    На наших уроках ми часто говоримо про те, для чого ми вивчаємо математику. Давайте переглянемо декілька слайдів.

  Слайд І.

  Математика в сузір’ї наук.

Ти визнана главою всіх наук –

Потрібна нам ти завжди, скрізь і всюди,

Без математики ми нині як без рук,

З тобою з казки дійсність творять люди.

  Слайд ІІ.

  Чи потрібно вивчати математику?

Математичні знання використовуються:

• у зв’язку з рухами сонця;
• із затемненням планет;
• із вимірюванням діаметрів і периметрів островів, океанів, гір;
• із обчисленням розмірів поселень і будівель жителів світу;
• у повсякденному житті.

     Слайд ІІІ.

     А чи пов’язана математика з іншими науками?

   Відомий датський фізик Нільс Бор говорив, що математика є чимось значно більшим, ніж наука, оскільки вона є мовою науки.

   А чи відомо вам, що сучасний світ називають епохою математичних знань?

   А чому?

       Слайд ІV.

    «Хімія – права рука фізики, математика – її око.»

                                         М. В. Ломоносов.

   А де ще крім фізики та хімії нам потрібна математика?

•                                            у географії;                                                  
•                                            у біології;
•                                            в економіці;
• у бухгалтерії;
• у медицині;
• у лісництві;
• у сільському господарстві;
• у спорті.

 

  Слайд V.

  Чи існує зв’язок математики з музикою, живописом, архітектурою?

  Попрацюйте і дайте відповідь на ці запитання через кілька уроків.

  У цьому вам допоможе:

• додаткова література;
• консультації вчителів – предметників;
• Інтернет;
• ваші власні дослідження і спостереження.

Вперед!!!

Удачі вам!!!

 

  На сьогоднішньому уроці ми познайомимося з вами з поняттям, яке допоможе вам відшукати зв’язок математики з багатьма іншими науками. Отже, тема нашого уроку…

 

  ІІІ.    Вивчення нового матеріалу.

 

    25 : 5 = 5          і             10 : 2 = 5 ,           тобто:

25 : 5 = 10 : 2         або         

 

    1.    Означення пропорції ( ст. 118 підручника)

    2.    Записи:         

 а : b = с : d                або                

            а    і    d   -   крайні члени пропорції;

            b  і    с   -   середні члени пропорції.

( Учні по черзі складають пропорцію і називають її крайні і середні члени).

  

    3.    Ці записи читаються…( ст. 118 підручника)

( На попередніх прикладах учнів читаємо пропорції різними способами).

          

           4.   Основна властивість пропорції ( ст. 118 підручника)

аd = bс

      ( Перевіряємо двома способами істинність складених раніше пропорцій).

          

5.    Історична довідка. ( повідомлення учня )

 

  Термін «пропорціональний» прийшов до нас з латинської  мови. Дослівно він означає: «такий, що має правильне співвідношення між частинами і цілим», «такий, що перебуває в певному відношенні до деякої величини».

  За допомогою пропорцій розв’язували різні задачі ще в стародавні часи. Повну теорію пропорцій було створено в стародавній Греції ще в ІV ст. до н. е. працями Евдокса Кнідського і Теетета.

  Відомо, що Фалес Мілетський (VІ ст. до н. е.), перебуваючи у Єгипті, обчислював висоту пірамід, вимірюючи їхню тінь і порівнюючи її з тінню стержня, взятого за одиницю вимірювання. Тобто, користувався пропорцією. 

  Сучасний запис пропорції за допомогою двокрапки і знака рівності ввів на початку

  18 ст. німецький математик і філософ Г.Лейбніц.

 

6.   Правила знаходження невідомого члена пропорції  ( ст. 119 підручника)

Наприклад,       3: х = 6 : 8,          х =

7.  Самостійна робота з підручником ( «Для тих, хто хоче знати більше ).

 

8. Один із сильних учнів пояснює, як він зрозумів прочитане і підкріплює свої знання на конкретних прикладах.

 

 

Фізкультхвилинка

 

Математична хвилинка

   

    Одне яйце вариться до готовності 5 хвилин. Скільки часу потрібно варити два яйця?

 

Екологічна хвилинка

 

    Синиця з’їдає за добу стільки комах, скільки важить сама. За місяць

( 30 днів ) вона знищує 6 000 г комах. Яка маса синиці?

                                                              (200 г )

 

ІV.    Формування вмінь і навичок.

 

Прочитати пропорції. Перевірити, чи вони правильні.       - № 663

 

Назвати крайні та середні члени пропорції. Скласти інші рівності, виходячи з основної властивості.                                          - № 664

 

Скласти пропорцію із даних чисел.                                 - № 666, 667

 

Чи правильна пропорція?                                                  - № 668

 

Знайти невідомий член пропорції.                               - № 665 (усно), 670

 

Додаткові вправи ( для кмітливих ):

1. Виходячи із правильної рівності

12 * 4 = 0,5 * 96, складіть 4 істинних пропорції.

2. Серед чисел 6, 9, 10, 12, 15 виберіть такі, щоб із них скласти істинну пропорцію.

                                             (6 : 9 = 10 : 15)

 

5. Підсумок уроку.

 

    Повторюємо зміст вивчених понять, звертаємо увагу на правильне читання пропорцій та вміння використовувати основну властивість пропорції для перевірки істинності пропорцій та для складання нових, спираючись на дану істинну пропорцію.

    Оцінюємо роботу окремих учнів на уроці.

 

 

 

6. Домашнє завдання.

 

  1.  Прочитати п.23 підручника та вивчити означення пропорції, основну властивість пропорції та правила знаходження невідомого члена пропорції.

  2.  Виконати : № 669, 671, 675, 684 /

  3.  Додаткове завдання: скласти дві істинні пропорції і утворити з них три нові пропорції.

 

 

 

 

 

 

 

 

 

 

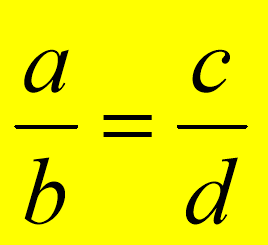
Урок №3

 

 

 

 

 

 

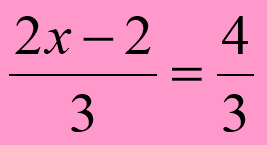
Мета уроку: закріпити знання та  вміння

                                 учнів,  набуті   на

                                 попередньому уроці;

                                 виробити вміння і   

                                 відпрацювати стійкі навички

                                 розв’язування рівнянь на основі  

                                 властивості пропорції;

                       виховувати культуру 

                       математичного запису;

                       розвивати логічне мислення       

                       учнів;

                      виховувати почуття     

                      колективізму;

                      розвивати інтерес до 

                      математики,  використовуючи  

                      задачі про світ живої природи.                                                                                              

Тип уроку:     формування вмінь і навичок

 

 

Хід уроку

 

І.    Актуалізація опорних знань.

 

Математичний диктант

     Закінчіть речення:

1.    «Рівність двох відношень називають…»

2.    «Якщо пропорція істинна, то добуток її крайніх членів дорівнює добутку…»

3.    Запишіть пропорцію 7 : 21 = 1 : 3. підкресліть однією рискою її крайні члени, а двома – середні члени.

4.    Доведіть істинність даної пропорції, використавши основну властивість.

5.    Знайдіть невідомий член пропорції 36 : х = 24 : 6.

6.    Із правильної рівності 3а = 5в складіть всі можливі пропорції.

 

   Всі учні пишуть математичний диктант у зошитах, а один учень – на відкидній дошці. Вчитель разом з учнями перевіряє правильність виконання на дошці, виправляє помилки і одночасно їх коментує. Після цього учні обмінюються зошитами і виконують взаємоперевірку системою  +, —. За кожне правильно виконане завдання – 2 бали.

 

ІІ.      Мотивація навчальної діяльності.

 

    Давайте разом згадаємо, де знання про пропорцію ми можемо використати у повсякденному житті. (Учні наводять приклади: у кулінарії, медицині, будівництві, картографії, природознавстві…)

   Виявляється, що на основі властивості пропорції та за правилами знаходження невідомого члена пропорції можна розв’язувати рівняння у математиці.

    Саме цим ми і будемо займатися на сьогоднішньому уроці.

 

ІІІ.    Вивчення нового матеріалу.

 

 Алгоритм розв’язування рівнянь виду    , де невідомий один із членів:

1. Записати основну властивість пропорції аd = bс.
2. Знайти невідомий множник.

 

Наприклад :                

                   

 (колективне розв’язання )

                                              х = 2

 

Фізкультхвилинка

 

Математична хвилинка

 

Розгадування анаграми.

 

  Розгадайте анаграми і вкажіть зайве слово, яке не відноситься до теми нашого уроку.

 

Неняшонвід    цопроряці    дравкат    нилеч

 

       (відношення    пропорція   квадрат   члени)  

 

Екологічна хвилинка

 

    Одна сова з’їдає за літо 1 000 польових мишей, зберігаючи  цим самим

1 т зерна. Скільки потрібно сов для збереження 5 т зерна?                                                                                               

                                                                    ( 5 сов )

 

 

ІV.    Формування вмінь учнів.

 

    Розв’яжіть рівняння:                                        № 672 (  0,3;   8,8;   10,5;  9;  9;  18 )

  

   Перші три рівняння учні розв’язують на дошці під керівництвом учителя, коментуючи кожен крок.

 

Робота в групах

 

    Решта рівнянь – змагання між рядами: кожен ряд працює над одним рівнянням. Перший учень, що правильно знайшов корінь рівняння, здобуває право бути консультантом у своїй групі, він допомагає своїм товаришам. Перемагає та команда, у якій всі учасники справилися із завданням.

 

Самостійна робота ( навчальна )

 

    Розв’яжіть рівняння:                                         № 676  ( 16;  69;  2;  31,8 )

 

Хто швидше? 

 

( перший учень отримує 12 балів, другий – 11 балів, третій – 10 балів )

 

                         

х = 1

                            

    V.    Підсумок уроку.

 

      Повторюємо алгоритм розв’язування рівнянь з використанням основної властивості пропорції. Звертаємо увагу на чіткість і правильність математичного запису.

     Оцінюємо роботу учнів на уроці, враховуючи результат за математичний диктант.

    

VI.     Домашнє завдання.

 

    1. Повторити за п. 23 означення пропорції та правила знаходження невідомого члена пропорції.

    2.  Вивчити за конспектом алгоритм розв’язування рівнянь на основі властивості пропорції.

    3.  Розв’язати рівняння  № 673,  677,  788 .

    4.  Додаткове завдання: прочитати рубрику «Для тих, хто хоче знати більше» ( ст. 120 ) про похідні пропорції із даних і показати на прикладах, що вони завжди істинні.

 

 

 

 

 

 

 

 

Урок №4

 

 

 

                           .          

 

Мета уроку: сформувати уявлення учнів про

                                 пряму  пропорційну залежність 

                                 величин, ознайомити із

                                 прикладами таких величин, що

                                 їх учні зустрічають у

                                 повсякденному житті;

                                 сформувати вміння  

                                 розв’язувати задачі цього

                                 типу складанням пропорції;

                                  виховувати культуру

                                  математичного запису;

                                  розвивати усний рахунок та 

                                  логічне мислення;

                                   показати практичне 

                                  застосування математичних

                                  знань.

Тип уроку:      засвоєння знань, умінь і 

                                  навичок.

Хід уроку

 

    І.    Актуалізація опорних знань.

 

1.  Теоретична розминка.

 

  1.  Давайте згадаємо все, що нам відомо про пропорцію. Я пропоную комусь із вас провести теоретичну розминку.

                      

                  (Один учень в ролі учителя)

 

Запитання:

1. Що називається пропорцією?
2. Яку назву мають члени пропорції?
3. Що можна робити з членами пропорції?
4. Яка основна властивість пропорції7
5. Яким математичним терміном можна замінити слово «відношення»?
6. Як знайти невідомий крайній член пропорції?
7. Як знайти невідомий середній член пропорції?
8. Який алгоритм розв’язування рівнянь з використанням основної властивості?

 

 

 

2. Усний рахунок

 

• Із даних чисел скласти істинну пропорцію і довести її правильність:

а)    за означенням пропорції;

б)    за основною властивістю пропорції.

6, 30, 5, 36;                  ( 6 : 36 = 5 : 30 );

3; 4,5; 8, 12;                 (4,5 : 3 = 12 : 8 )

• Серед даних чисел якимось чином потрапило зайве число. Знайдіть його, а з тих чисел, що залишаться, складіть істинну пропорцію.

6, 15, 12, 10, 9.

( зайве – 12;          6 : 9 = 10 : 15 )

 

• Знайти значення Х, при якому будуть істинні пропорції.

а)                             б)  ;

в)  ;                          г)   .

 

 

 

 

 

    ІІ.    Мотивація навчальної діяльності.

 

    У повсякденному житті нам часто зустрічаються величини, що пов’язані між собою:

• вартість покупки та її кількість;
• кількість товару і його маса;
• час і відстань при сталій швидкості.

    Ці величини перебувають у певній залежності одна від одної. Що це за залежність і як знаходити одну величину, якщо відома інша, ми і будемо з’ясовувати на сьогоднішньому уроці.

 

    ІІІ.    Вивчення нового матеріалу.

 

    1.    Означення прямо пропорційної залежності величин  ( ст. 124 підручника)

  

    Зауваження:  такі величини називаються прямо пропорційними, тобто для них можна скласти істинну пропорцію.

 

    2.    Наведіть приклади прямо пропорційних величин, що ви зустрічали у житті

                                               ( приклади учнів)

 

3.   Поняття прямо пропорційних величин допоможе нам навчитися розв’язувати задачі, схожі на задачі у темі «Знаходження дробів від числа та числа за його дробом». Але тепер ми будемо вчитися розв’язувати їх, складаючи пропорції.

 

    Колективне розв’язання задачі за допомогою пропорції під керівництвом учителя  ( рубрика «Прочитайте» на ст. 124 підручника, задача 1 )

 

↓  10 кг яблук    -----     8 кг пюре;  ↓

 44 кг яблук    -----     х кг пюре.  

 

      Зауваження:            звертаємо увагу на правильне складання пропорції та запис розв’язання. Слідкуємо, щоб учні усвідомили, що перед складанням пропорції необхідно пересвідчитися в тому, що величини є дійсно прямо пропорційними, і робили це не формально. Тільки після цього стрілками показуємо, що зміна першої і другої величини одного напрямку ( перша зменшилась і друга зменшується у стільки ж разів, тому стрілки умовно спрямовані в один  бік) і складаємо рівняння у вигляді пропорції та розв’язуємо його:                        

х = 35,2 кг

 

     4.    Самостійна робота з підручником ( рубрика «Прочитайте» на ст. 124 , задача 2 )

   

5.   Інформація для сильних учнів:

      величини х і у, залежність між якими можна виразити формулою

у = k х, де k – число, що не дорівнює 0,

      є прямо пропорційними.

 

Фізкультхвилинка

 

Математична хвилинка

 

  Три курки за три дні несуть 3 яйця. Скільки яєць знесуть:

а)  6 курей за 6 днів?

б)  4 курки за 9 днів?

                                             (12 яєць; 12 яєць)

 

Екологічна хвилинка

 

  Відомо, що 1 га лісу виділяє стільки кисню, що його вистачає для дихання 200 чоловік. Скільки потрібно лісу для міста, в якому 15 000 чоловік?                                                                       

                                                                      (75 га)

 

ІV.    Формування вмінь та навичок.

 

    Які з поданих величин прямо пропорційні?                       № 678 (усно)

 

    Розв’язування задач       № 688  (19,5 г), 

              689  (92,5 кг),

              692  (200 кг),

              693  (1 т),

              694  (45 костюмів),

              696  (30 см),

              698  (1 : 50).

 

    Хто швидше?      № 703   («Нива» більше на 7 л)

 

(перший учень отримує 12 балів, другий – 11 балів, третій – 10 балів)

 

  

     V.     Підсумок уроку.

 

    Повторюємо означення прямо пропорційних величин, наводимо приклади. Звертаємо увагу на те, як знання про пропорцію допомагають розв’язувати задачі. Наголошуємо на правильності складання пропорції за умовою задачі та на її розв’язанні.

    Учні виділяють своїх товаришів, які були найбільш активними і оцінюють їх роботу на уроці, мотивуючи свої оцінки.

 

 

 

 

     VI.    Домашнє завдання.

 

  1.  Прочитати п.24 підручника та вивчити означення прямо пропорційної залежності.

   2.  Виконати : № 690, 691, 695, 697 /

   3.  Додаткове завдання:

знайти товщину аркуша паперу вашого підручника з математики, виконавши необхідні вимірювання та зробивши певні обчислення.

 

 

Урок №5

 

 

 

 

 

 

 

 

 

                   .          

Мета уроку: закріпити поняття

                                «відношення» та  «пропорція»;

                            розвивати вміння та навички 

                            при розв’язуванні задач на      

                            пропорції;

                            показати учням загально-

                            інтелектуальне значення  

                             математики;

                                   розширяти кругозір учнів,

                                  розвивати  в них творчу та

                                   пізнавальну  активність;

                                   розвивати вміння пізнавати

                                   закони краси та гармонії 

                                   навколишнього середовища;

                                   виховувати почуття      

                                   колективізму та 

                                   впевненості у своїх силах.

Тип уроку: застосування знань, умінь і навичок.

Хід уроку

 

    І.    Мотивація навчальної діяльності.

 

      На сьогоднішньому уроці ми будемо говорити про застосування математичних знань у повсякденному житті.

    Ми з вами поринемо у світ пропорції, будемо розв’язувати задачі і спробуємо знайти відповідь на запитання: «Що спільного має пропорція з живописом, скульптурою, архітектурою, картографією, хімією, музикою?»

 

    Оскільки ви вже багато знаєте і вмієте, то сьогодні я вам пропоную відчути себе кореспондентами різних  наукових журналів, які займаються саме цими питаннями і готові поділитися своїми досягненнями, обмінятися досвідом.

   Отже, ми знаходимося в науково-дослідницькому інституті, який займається питанням «Золотого перерізу», на прес-конференції, присвяченій даній темі.  На нашій прес-конференції представляють своє видання кореспонденти 4-х наукових журналів «Інтелект», «Аргумент», «Числові мозаїки» та «Наукова скарбничка». Всі співробітники працювали над різними питаннями даної теми і сьогодні пропонують їх на обговорення та на знаходження нових рішень.

 

ІІ.    Актуалізація опорних знань.

 

      Перед початком конференції необхідно пройти реєстрацію учасників.

  Заповніть свої реєстраційні картки.

1.   Тестові завдання.

 

 

 

 

 

 

 

 

 

 

 

 

 

Ключ до тесту:

1	2	3	4
Б	Б	А	Г

 

              ( Взаємоперевірка – за кожну правильну відповідь 3 бали )

 

  Отже, учасники конференції пройшли реєстрацію і готові до роботи.

 

  Під час конференції ви повинні бути дуже уважними. Перевіримо вашу увагу.

 

2.   Усний рахунок

 

• Із даних чисел скласти істинну пропорцію і довести її правильність:

а)    за означенням пропорції;

б)    за основною властивістю пропорції.

4,  15,  5,  12;                  (4 : 5 = 12 : 15);

• Знайти значення Х, при якому будуть істинні пропорції.

а)                             б)  ;

в)  ;                           г)  

 

 

  Також кореспонденти повинні вміти точно і правильно висловлювати свою думку, формулювати запитання і давати чітку відповідь. Отже, з цього і почнемо.

 

  Робота в парах                       

(інтерв’ю учнів по означенню пропорції та основній  властивост )

 

  Мікрофон                               

(кілька учнів озвучують)

 

    ІІІ.    Вдосконалення вмінь і навичок.

 

    1.  А тепер в роботу включаються наші співробітники. Кожне видання повинно назвати якнайбільше прикладів застосування знань про пропорцію.

                          (називають по черзі)

 

1. Тепер я пропоную головним редакторам обрати задачу на пропорцію із

чотирьох галузей і розв’язати її спочатку із своїми співробітниками, а потім пояснити усім присутнім.

 

 

 

 

 

Задачі на відношення та пропорції.

(робота в групах)

 

1. Виробництво

   

    Із 400 кг молока одержали 84 кг вершків. Скільки вершків одержать із

1 т молока?

                                                             (210 кг)

                                                           

2. Географія

 

    Довжина автомобільної траси від нашого села до обласного центру 180 км. Яка довжина цієї траси на карті з масштабом 1 : 10 000 000?

                                                                       (1,8 см)

 

3. Хімія

     

       У 150 г розчину міститься 5 г солі. Скільки солі міститься у 900 г такого ж розчину?

 

                                                                             (30 г)

 

 

 

 

4. Природознавство

   

     Для захисту лісу від будь-яких шкідників необхідно мати 6 мурашиних гнізд на 1 га. Скільки мурашиних гнізд потрібно для захисту лісу площею 25 га?

                                                                     (150 гнізд)

              

  3.   Де ще в математиці, крім задач, використовуються пропорції? Звичайно, при розв’язуванні рівнянь.

 

Розв’язування рівняння.

( який журнал справиться швидше )

 

* (2х -2) = 12;

2х -2 = 18;

2х = 20;

х = 10.

 

 

 

Фізкультхвилинка

 

Математична хвилинка

    Чи знаєте ви пропорцію? Звичайно, знаєте. Давайте перевіримо.

 

а)     Одна табуретка важить 3 кг, а скільки важать дві такі табуретки?

                                                                 Так, 6 кг.

 

б)    Півень, стоячи на одній нозі , важить 3 кг. Швидко скажіть, скільки він важитиме, стоячи на обох ногах?

                                                                       (3 кг)

 

в)      Верблюд упродовж 1 год витримує вантаж масою 200 кг. Упродовж якого часу він витримає вантаж масою 20 т?

                               (не витримає такого вантажу)

 

 

 

Екологічна хвилинка

 

    1т паперу, переробленого з макулатури, збереже 20 дерев. Скільки потрібно зібрати макулатури, щоб зберегти 1 дерево?                                                                                

                                                                           (50 кг)

 

 

 

    ІV.    Застосування знань про пропорцію.

 

    У нашому селі є визначна річ – Башта, висоту якої ви не знаєте. У вас є фото цієї башти. Як допоможе це фото для визначення висоти башти? Підійти до башти ви можете, а виміряти висоту – ні.

             

   ( обговорюють у групах і пропонують свої варіанти )

 

( Треба виміряти довжину сторони основи і висоту башти на фотографії, а потім довжину сторони основи самої башти. Ураховуючи, що фотографія дає зображення, подібне до натури, висота башти буде в стільки разів більша від її висоти на фотографії, у скільки разів сторона основи башти більша від її зображення на фотографії.)

 

    V.    «Золота пропорція».

 

    На початку вивчення даної теми ми ставили перед собою питання: чи є щось спільне між пропорцією і мистецтвом, пропорцією і скульптурою, пропорцією та музикою? Ви проводили свої дослідження, цікавилися додатковою літературою. Кожна група займалася конкретною проблемою. І сьогодні настав час поділитися результатами своєї праці.

 

    Одну з відповідей на поставлені запитання допоможе нам знайти кросворд.

  

Кросворд

 

 

                                                              

 

 

 

 

 

 

 

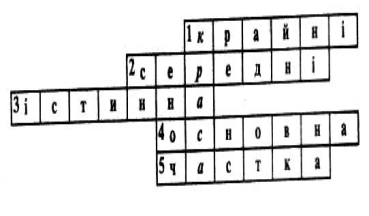
1.Члени пропорції.

2. Члени пропорції.
3. Як називається пропорція, значення лівої і правої
4. частини якої є одне й те саме число?
5. У правильній пропорції добуток крайніх членів дорівнює добутку середніх. Як називається ця властивість пропорції?
6. Яким математичним терміном можна замінити слово «відношення»?

 

  Ми знайшли одну відповідь на поставлене питання – це краса.

          (Головні редактори звітують про свою роботу)

 

Історична довідка

 

( науковий журнал «Аргумент» )

                                

     Поняття пропорціональності мало і має широке застосування в мистецтві, музиці та архітектурі. Воно означає додержання певних співвідношень між окремими частинами споруди, картини, скульптури чи музичного твору, яке справляє найприємніше враження.

  Поняття відношення і пропорції виникло в далекій давнині, про що свідчать будівлі стародавнього світу, які вражають пропорційністю своїх форм.

  Дотримання певних співвідношень у математиці називають «золотим поділом» або

«золотим перерізом».

   Що це за відношення? Його можна пояснити на прикладі поділу даного відрізка.

А                                             С                             В                                                                                        

 

  Якщо ми маємо довільний відрізок АВ і точка С ділить його на дві частини так, що відношення всього відрізка АВ до його більшої частини АС буде дорівнювати відношенню його більшої частини АС до меншої СВ, то даний відрізок поділений за правилом «золотого перерізу».

= 1,618

  Саме Леонардо да Вінчі назвав цей переріз «золотим».

  А Лука Пачіолі присвятив цьому питанню книжку «Божественна пропорція»

 (1509 р.)

  Значну увагу приділяв цьому перерізу Й.Кеплер, який пов’язував його з будовою Всесвіту. Вважали, що золотий переріз є нібито універсальною пропорцією, яка властива як найдосконалішим витворам природи, так і найкращим творам мистецтва. Йому надавали містичного значення.

  Багато предметів прямокутної форми (зошити, підручники) мають форму, близьку до «золотої пропорції». Тобто, якщо довжину зошита поділити на його ширину, то це відношення       ≈ 1,618.

 Про  важливість «золотого перерізу» говорять слова Й.Кеплера:

«Геометрія володіє двома скарбами – теоремою Піфагора і «золотим перерізом», і якщо перше з них можна порівняти з мірою золота, то друге – з коштовним каменем.»

 

Пропорція у мистецтві

 

( науковий журнал  «Інтелект» )

 

    Картина Леонардо да Вінчі «Джоконда» довгі роки приваблює своїх шанувальників і привертає увагу дослідників. Вона, як і багато інших шедеврів мистецтва виконана за всіма канонами краси та гармонії. В ній зберігається «золота пропорція».

  Існує багато версій про історію цього портрету. Ось одна із них.

 

  Одного разу Леонардо да Вінчі отримав завдання від банкіра Франческо де ле Джокондо написати портрет молодої жінки, його дружини – Мони Лізи. Жінка не була красива, але в ній зачаровувала простота та невимушеність. Леонардо згодився написати портрет. Жінка була засмучена, але Леонардо розповів їй казку, і обличчя її засяяло по-іншому.

 

 

 

 

Казка

  Жив собі один бідняк, і було в нього 4 сина: троє розумних, а один ані так, ані сяк. От прийшла за батьком смерть. Перед тим, як попрощатися із життям, він покликав до себе дітей і сказав: «Сини мої, скоро я помру. Як тільки поховаєте мене, зачиніть хатину і йдіть на край світу шукати собі щастя. Нехай кожен з вас чому-небудь навчиться, щоб зміг прогодувати сам себе.» батько помер, а сини розійшлись по білому світу, і домовились через 3 роки повернутися на галявину до рідного двору.

  Прийшов перший брат, який навчився теслярському мистецтву, зрубав він дерево і витесав з нього дівчину, відійшов трохи і чекає.

  Повернувся другий брат, він вмів шити, побачив дівчину, і в одну мить зшив для неї чарівну сукню із шовку.

  Третій брат прикрасив дівчину золотом та коштовностями – він був ювеліром.

  Нарешті прийшов четвертий брат. Він не вмів майструвати чи шити, вмів тільки слухати, що говорить земля, дерева, трави, звірі та птахи, знав хід небесних світил і ще вмів співати чарівні пісні. Він заспівав пісню, від якої заплакали навіть брати. Піснею цією він оживив дівчину і вона посміхнулась.

  Брати кинулись до дівчини і кожен кричав їй одне і те саме: «Ти повинна бути моєю дружиною». Та дівчина їм відповіла: «Ти мене зробив – будь мені батьком. Ти мене одягнув, а ти прикрасив – будьте ж мені братами. А ти, що вдихнув у мене життя і навчив радіти сонцю, квітам, ти один мені потрібен на все життя».

 

  Закінчивши казку, Леонардо поглянув на Мону Лізу, її лице випромінювало світло, очі сяяли. Потім, немов прокинувшись після сну, вона зітхнула, провела по обличчю рукою і без слів пішла на своє місце, склала руки і прийняла звичний вигляд. Але діло було зроблено – художник розбудив байдужу статую: посмішка блаженства повільно зникла з її обличчя, залишилась десь у куточках рота, і це робило обличчя чарівним, загадковим, як у людини, яка дізналась величезний секрет, оберігала його і не змогла стримати торжества. 

 

  Дотримано «золотої пропорції» у таких шедеврах, як «Сосновий бір» І.І.Шишкіна,

«Незнайомка» І.М.Крамського, «З’явлення Христа народу» О.А.Іванова та ін.

 

 

Пропорція у скульптурах

 

( журнал «Наукова скарбничка» )

 

    Ми всі неодноразово чули вислів «пропорціонально збудована людина». Що він означає?

  Чим  приваблюють нас відомі статуї Аполлона Бельведерського, Венери Мілоської, Зевса Олімпійського, Афіни Парфенос?

  На ці питання ми знайшли відповідь тоді, коли більше дізналися про «золотий поділ».

  Виявляється, що всі ці статуї виконані за правилом «золотої пропорції». Тобто:                      а) відношення висоти всієї статуї до її висоти від підлоги до талії дорівнює 1,618;

б) відношення висоти вище талії до висоти між головою і піднятою над головою рукою ( в напівзігнутому положенні) також дорівнює 1,618.

 

   Готуючись до сьогоднішнього уроку, ми провели невеличкий «конкурс краси» і  перевірили, чи близькі ми до Венери Мілоської чи Аполлона Бельведерського. Результати виявилися такі:

    (учні знайомлять із своїми даними ).

 

 

Пропорція у музиці

 

(науковий журнал «Числові мозаїки»)

   

    Наша група дізнавалася про зв’язок між математикою та музикою, зокрема, ми з’ясовували, що спільного між музикою та пропорцією.

    Виявляється, що стародавні греки називали вчення про відношення і пропорції музикою, яку вважали галуззю математики. Вони знали, що слабше натягнута струна дає нижчий («товстіший») звук, а тугіше натягнута струна – вищий звук. Але в кожному музичному інструменті є не одна, а кілька струн. Щоб усі струни під час гри звучали «узгоджено», приємно для слуху людини, їхні довжини (а за однакових довжин – товщини) повинні перебувати у певному відношенні. Саме тому вони й вважали музику галуззю математики.

     Ми підготували математичний бюлетень по даній темі, а також пропонуємо переглянути слайди, підготовлені нашою групою.

    (учні на комп’ютері звітують про свою роботу).

 

 

    V.  Підсумок уроку.

 

    Я дякую всім за роботу на уроці. Гадаю, що сьогодні ви дізналися багато цікавого і подивилися на математику трішки іншими очима.

    Щоб оцінити роботу кожного із вас на уроці, я прошу заповнити «Табель успішності» (кожен учень виставляє оцінку всім членам своєї групи, в тому числі і собі, а вчитель добавляє свою оцінку, враховує результати тесту і виводить середній бал).

 

     Закінчити урок я хочу такими словами:

 

«Математика – цариця наук. Її коханий – істина, її вбрання – простота та ясність. Палац цієї володарки оточений тернистими заростями і, щоб досягти його, кожному треба продертися крізь хащі. Випадковий подорожній не знайде в її палаці нічого привабливого. Краса його відкривається лише розуму, який любить істину і загартовується в боротьбі з труднощами.»

 

    Бажаю всім присутнім долати труднощі не лише при вивченні математики, а й повсякденному житті.

 

    VІ.    Домашнє завдання.

    Для закріплення ваших знань я пропоную вдома:

1)  повторити всі правила і означення по даній темі;

2)  кожному скласти і розв’язати 2 задачі на пропорцію;

          3)  провести «Конкурс краси» у своїй родині.

 

 

 

 

 

 

 

 

 

 

Література

 

1. Закон України «Про освіту»
2. Нова програма 12-річної школи 5 – 12 класи. Математика. – К.: Ірпінь – 2005.
3. Г.М.Возняк, М.П.Маланюк. Взаємозв’язок теорії з практикою в процесі вивчення математики. – К.: Радянська школа, 1989.
4. О.Г.Черватюк, Г.Д.Шиманська. Елементи цікавої математики на уроках математики. – К.: Радянська школа, 1968.
5.  Г.Янченко, В.Кравчук. Математика, 6 клас; Тернопіль, видавництво «Підручники і посібники», 2006.