Геометрия – 9 класс

 

Тема: Решение треугольников (12 часов).

Цель: Выработать умение решать основные задачи на нахождение элементов произвольных треугольников.           

 

Учащиеся должны:

 

знать                - теоремы косинусов и синусов и следствия из них

              -   алгоритмы решения произвольных треугольников

уметь               - решать задачи, используя алгоритмы решения

                            треугольников

 

№	Тема	Тип урока
1-2	Теорема косинусов и следствие из неё. Теорема синусов и следствие из неё	Урок изучения нового материала и первичное закрепление
3-4	Решение треугольников	Урок комплексного применения знаний и умений
5-6	Решение треугольников	Урок комплексного применения знаний и умений
7-8	Решение треугольников	Урок комплексного применения знаний и умений
9-10	Решение прикладных задач	Урок обобщения и систематизации знаний и умений
11	Решение треугольников	Урок  актуализации знаний и умений.
12	Контрольная работа	Урок контроля и коррекции знаний и умений.

 

 

 

 

 

 

 

Урок № 1-2

Тема: Теорема косинусов и следствие из нее.

         Теорема синусов и следствие из нее.

 

Цель урока. Создать условия для усвоения основных теорем, дающих возможность решать треугольники; способствовать осознанию основного теоретического материала.                                           Создать условия для формирования умений применять     полученные знания к решению задач.

Создать условия для развития у учащихся навыков                       самоконтроля; формирования познавательной активности, воспитания культуры умственного труда, коммуникабельности.

Тип учебного занятия: Урок изучения нового материала и первичного закрепления.

Ход урока.

I. Оргмомент.

 - Приветствие.        

Пусть каждый день и каждый час

Вам новое добудет.

Пусть добрым будет ум у вас,

А сердце умным будет.

• Проверка отсутствующих.
• Установка «Внимание!» 

       Математику нельзя выучить, наблюдая, как это делает сосед.     А. Нивер.

 

II. Целеполагание  и мотивация.

 Приступая к изучению нового раздела курса геометрии «Решение треугольников», необходимо раскрыть его содержание и показать, насколько учащиеся уже знакомы с данным вопросом. Треугольник является одной из основных геометрических фигур, а многие другие можно разбить на треугольники. Поэтому способы вычисления элементов треугольника особенно актуальны.

 

III. Актуализация.

1.  Изобразите и обозначьте основные элементы треугольника.
2. Чем и в каких единицах измеряют углы и стороны треугольника?
3. Напишите, чему равен косинус острого угла прямоугольного треугольника.
4. По четырёхзначным математическим таблицам определите SIN46º 12´, COS 18º 6.´
5. В прямоугольном треугольнике, зная гипотенузу с и острый угол α, найти

а, в, β

 

            с

а                     

                              

          в

Самопроверка (ответы на доске).

IV. Первичное усвоение материала.

Исследуем зависимость между сторонами и углами в произвольном треугольнике. Практическая работа в группах. Каждая группа получает задание и набор разнообразных фигур.

Задания:

Группа 1. «Открытие» теоремы косинусов.

1) В Δ АВС  выразить вектор   через векторы и .

                        С

                    в                               а

А

 

 

                              с                             В      

2) Возведите обе части получившегося равенства скалярно в квадрат.

3)Выразите скалярное произведение векторов через их абсолютные величины (т. е. длины сторон треугольника) и угол между ними. Сделайте вывод.

Группа 2. «Открытие» теоремы синусов.

1. Измерить стороны а, с и углы α, γ  данных треугольников.
2. Пропорциональны ли длины сторон синусам противолежащих углов?

Вычислите а:SINα, в:SIN β , с:SIN γ, сравните полученные значения.

3. Сформулируйте полученный вывод.

   Группа 3.  «Открытие» следствия из теоремы косинусов.

1. Измерьте длины сторон а, в и диагоналей d_1, d₂  параллелограммов.
2. Выразите сумму квадратов диагоналей через его стороны и углы.
3. Сделайте вывод.

Группа 4. «Открытие» следствия из теоремы синусов.

1. Измерить углы 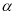и 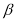в данных треугольниках. (На всех моделях  <)
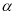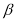2.  Определите 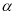Sin   и Sin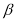, сравните полученные значения.
3.  Сделайте вывод.

V. Осознание и осмысление учебной информации.

Каждая группа делится своим «открытием». Учитель подводит итоги, дополняет, анализирует, доказывает.

      Первая группа рассказала нам теорему, впервые доказанную известным математиком аль Бируни (973-1048 г.г.), и называемую теоремой косинусов. Учитель доказывает теорему.

      Вторая группа рассказала теорему, доказанную выдающимся азербайджанским ученым Насирэддином Туси (1201-1274 гг.), и называемую теоремой синусов.

Учащиеся оформляют в тетрадях конспекты.

VI.Первичное закрепление учебного материала.

1. Используя теорему косинусов, запишите выражение квадрата каждой стороны треугольника через две другие и косинус угла между ними.
2. Найдите условие, при котором  авCos=0.
3. Используя теоремы,  выведите формулу  для вычисления одного неизвестного элемента треугольника, если известны: 1) а, в и 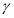 ;                2) а, в и 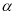;  3) а, в и с.
4. Исследуйте изменение стороны а при возрастании угла 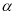от 0º до 180º (при постоянных в и с)
5.  Составьте задачи, для решения которых можно использовать теорему косинусов.
6.  Составьте задачи, для решения которых можно использовать теорему синусов.
7. Решите задачи по готовым рисункам.

 

       

                         х                                                                х

              45º                                                           135º

                                                                                                   3

          3

 

 

                                                                                              4                           

        2                              2

                                                                                              х

              60º

                                   х                                                            5

 

8. Докажите, что в теореме синусов каждое из трёх отношений а:SINα, в:SIN β , с:SIN γ  равно2R, где R -  радиус окружности, описанной около треугольника.
9. Найдите диагонали параллелограмма, если они относятся как 8:9, а стороны равны 11 см и 13 см.

VII. Информация о домашнем задании.

Выучить конспект. Ответить на вопросы 1 - 4 к §12. Решить № 1, 2, 5, 12.

По желанию подготовить сообщение о математиках, доказавших теоремы синусов и косинусов.

VIII.  Рефлексия (подведение итогов урока).

 

 

 

 

 

Урок № 3-4

Тема: Решение треугольников

Цель урока: Создать условия для применения знаний и умений учащихся в знакомой и новой учебных ситуациях.                                                                                                                                                        

Создать условия для развития математической речи учащихся и навыков культуры математических записей.                                                                                             

Создать условия для воспитания интереса к математике, таких                       черт характера, как старательность, самостоятельность,                    коммуникабельность.

                                   Ход урока:

1. Оргмомент.

   -Приветствие.

   -Проверка отсутствующих.

   -Установка «Внимание!»

   Кто с детских лет занимается математикой, тот развивает свой мозг, воспитывает волю.  В.М. Брадис

2. Целеполагание и мотивация.
3. Актуализация.

(За каждое выполненное задание ученики выставляют заработанное количество баллов на полях тетради.)

1. Найдите в учебнике и прочитайте вслух формулировки теорем синусов и косинусов. (0,5 балла)
2. Взаимопроверка (рассказать теоремы друг другу по очереди). Работа в парах. (по 0,5 балла)
3. Изобразите и обозначьте основные элементы треугольника. (0,5 балла)
4. Запишите формулу для теоремы синусов. (1 балл)
5. Выразите сторону а треугольника АВС  через стороны в и с и угол ( 1 балл)

4. Применение знаний.

   Устно:

      1)Пользуясь формулой а²=в²+с²-2всСоs, исследуйте, как изменяется сторона а  при возрастании угла от 0º до 180 º (при постоянных в и с)

      2) При каких  квадрат стороны треугольника, лежащей против этого угла                         

• меньше суммы квадратов двух других сторон ( - острый)
• равен сумме квадратов двух других сторон ( - прямой)
• больше  суммы квадратов двух других сторон ( - тупой)

      3) Не вычисляя величины углов треугольника, укажите вид каждого, относительно углов:

           - 7; 8; 12.               (остроугольный)

           - 0,3; 0,4; 0,5.        (прямоугольный)

           - 15; 15; 15.           (остроугольный,  равны все углы)

           - 8; 10; 12.              (тупоугольный)

     Письменно: (диф. самост. работа)

Задание 1. 

На 3 балла. Доказать, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

На 2 балла. Вычислить больший угол _ΔАВС, если а=3, в=4, с=6.

На 1 балл. Вычислить неизвестную сторону _ΔАВС , если а=7, в=10, =56º 29`.

Задание 2.

На 3 балла. Диагональ параллелограмма длиной m образует со сторонами этого параллелограмма углы и . Выразите длины сторон параллелограмма через m, и .

На 2 балла. Вычислите угол , если а=109, =33º 24`, =66º 59`.

На 1 балл. Вычислить неизвестную сторону _ΔАВС , если а=109, =33º 24`, =66º 59`.

Физкультминутка:

·Если вы уверены, что квадрат гипотенузы равен сумме квадратов катетов, встаньте.

  ·Если вы уверены, что теорема Пифагора применяется только к остроугольному треугольнику, повернитесь направо.

 ·Если вы уверены, что сумма углов треугольника 180º, поднимите руки.

 ·Если вы уверены, что сумма острых углов прямоугольного треугольника

90º, повернитесь налево.

   ·Если вы уверены, что теорема синусов справедлива для прямоугольного треугольника, поставьте руки в стороны.

 ·Если вы уверены, что теорема косинусов справедлива только для остроугольного треугольника, подпрыгните. 

 ·Если вы уверены, что в треугольнике против равных сторон лежат равные углы, садитесь.

 Письменно:

 1. Определите вид треугольника, у которого стороны относятся как 29:25:38

 2. Докажите, что если в треугольнике медиана совпадает с биссектрисой,

то он равнобедренный.

 3. В треугольнике АВС B >C>A. Назовите стороны треугольника в порядке убывания.

 4.  АВ <AC <BC. Назовите углы в порядке возрастания.

 5. В – тупой. Какая сторона треугольника АВС наибольшая?

  V.  Информация о домашнем задании.

Решить №18, 19, 20. Уметь отвечать на вопросы 1-4 к §12. По желанию придумать 3 вопроса, которые ты хотел бы задать учителю по теме “Решение треугольников”. По особому желанию составить физкультминутку.

  VI.  Рефлексия (подведение итогов урока)

 

 

 

Урок № 5-6

Тема: Решение треугольников

Тип учебного занятия: Урок комплексного применения знаний и умений

Цель урока: Создать условия для применения знаний и умений, учащихся в незнакомой учебной ситуации.                                                                                                                                                         

Создать условия для развития навыков самостоятельной работы, умение анализировать и обобщать.                                                                                               

Создать условия для воспитания старательность, коммуникабельность уверенность в своих силах.

                                   Ход урока:

1. Оргмомент.

   -    Приветствие

• Проверка отсутствующих
• Установка «Внимание!»

Чтобы переварить знания, их нужно употреблять с аппетитом.        А. Франс

2. Целеполагание и мотивация.

А, как известно аппетит приходит во время еды. Поэтому сегодня мы выделим основные задачи, и выработать алгоритмы их решений.

3. Актуализация.

                                         Верю - не верю

1. Сумма углов любого треугольника равна 180º.
2. Внешний угол любого треугольника равен сумме двух внутренних углов, не смежных с ним.
3.  В прямоугольном треугольнике сумма острых углов равна 90º.
4. В треугольнике против равных сторон лежат равные углы.
5. Равные наклонные имеют равные проекции.
6. Перпендикуляр короче наклонной, выходящей из той же точки.
7. Косинус угла зависит только от величины угла.
8. Стороны треугольника пропорциональны синусам прилежащих углов.
9. В остроугольном треугольнике сумма любых двух углов больше 90º.
10. В равнобедренном треугольнике основание больше боковой стороны, если угол, прилежащий к основанию больше 60º.
11. Если квадрат стороны треугольника равен неполному квадрату суммы двух других сторон, то эта сторона лежит против угла 120º.
12. Если сторона треугольника лежит против угла 60º, то ее квадрат равен неполному квадрату разности двух других строк.
13. Треугольник со сторонами 0,3х, 0,4х, 0,5х тупоугольный.
14. Равнобедренный треугольник не может быть прямоугольным.

IV.     Применение знаний

1) Задача: Решить треугольник – это значит, зная несколько его основных элементов, вычислить остальные.

    Вопрос: 1.Сколькими элементами определяется треугольник? (тремя как минимум,  и один  из них – линейный)

               2. Достаточно ли трёх углов?

2)Решение треугольников в общем виде.(Составление алгоритмов)

Работа в парах.

По одному человеку у доски предлагают составленный алгоритм, остальные обсуждают ответ.

Записать алгоритмы в тетрадь:

Задача 8

а=12        c=?

в=5          =?         

=120    =?

Задача 9

а=15       =?

в=24       =?

с=18       =?

Задача 10

    в=9           а=?

   с=17         =?

   =95        =?

Задача 11

а=7          b=?

=35       c=?

=100     =?

Задача 12

а=80

=97

R=50

Найти все неизвестные стороны и углы.

5. Информация о домашнем задании

Выучить алгоритмы решения задач, решить №26-29(1). По желанию: придумать загадки, четверостишья по теме «Решение треугольников».

6. Рефлексия (подведение итогов урока)

 

 

 

Урок № 7-8

Тема: Решение треугольников

Цель урока: Создать условия для закрепления умений применять знание  теоремы косинусов и теоремы синусов к решению более сложных задач.

Создать условия для развития навыков самостоятельной работы,                      логического мышления.

 Создать условия для воспитания коммуникабельности.

 Тип учебного занятия: Урок комплексного применения знаний и умений

Ход урока:

І. Оргмомент.

 Приветствие.                                                                           

 Проверка отсутствующих.                                         

Установка «Внимание!»

                                                          Какая радость особенно велика?

                                                          Когда удаётся достичь желанного.

                                                                                     Фалес Милесский.    

ІІ. Целеполагание и мотивация.

III. Актуализация опорных знаний.

Математический диктант с взаимопроверкой (ответы записаны заранее на закрытой доске.)

1.Изобразите и обозначьте основные элементы треугольника. 

2.Запишите формулу для нахождения . 

3. Две стороны треугольника равны m и k. Найдите третью сторону, лежащую против угла 60°.  

4.Какого размера может быть угол, лежащий против стороны с, если квадрат этой стороны равен сумме квадратов двух других сторон?  

5.В   Δ АВС   АВ > АС > ВС. Запишите углы этого треугольника в порядке возрастания. 

6.В каком случае длина стороны с Δ АВС будет наибольшей: если угол γ острый, тупой или прямой?                

 

  Ответы на доске:

1.                    

                       В                                             

 

              с               а

 

                      

        А            в             С                                  0,5 б.    

 

2.Cos=                                                   0,5 б.                       

 

 

3.m² +k² - mk                                                                   1б.

 

4.90º                                                                              1б.

 

5. А, В,С                                                           0,5 б.       

 

6. - тупой.                                                                  0,5 б.

 

IV. Применение знаний.

3.1 Задача о Пизанской башне.

В Италии находится Пизанская башня, на которой в своё время проводил исследования Галилео Галилей. А ещё она известна тем, что с каждым годом всё больше наклоняется к земле. Каждый предмет имеет свой центр тяжести, и наклонившись, он упадёт тогда, когда перпендикуляр, проведённый из центра тяжести к плоскости основания выйдет за пределы основания. Вычислите угол наклона башни, при котором она может упасть, если расстояние от центра основания башни до её центра тяжести равно 16,7 м, а диаметр основания башни 18,9 м. Что для этого нужно сделать?

 

 

                                                                         16,7

 

                                                                                                                    

                              

                                                                                 9,4

Cos  0,5629  ;  = 55°45'                            2 б.

3.2. Биссектриса прямоугольного треугольника делит гипотенузу на отрезки 20 см и 15 см. Найдите периметр треугольника.     3 б.   

3.3. Две стороны треугольника, разность которых равна t, лежат против углов 30° и 45°. Найдите длины этих сторон.               3б.  

3.4. Составьте план решения задачи устно, а дома оформите решение в тетради.

                   B                         C

 

 

    A    D               

ABCD – трапеция.

BC = 23                            

AD = 43 

A = 76°

D = 63°

Найти: AC и BD.

                         В

 

          А

                                           С

Р_∆АВС = 38 см

А = 48°

В = 53°

Найти: АВ, ВС, и АС

             В                                           С

 

 

 

 

А                                            D

ABCD – параллелограмм

AB = BD

AD = 10 м

Найти: P_ABCD

V. Информация о домашнем задании

Оформить в тетради решение задач. По желанию придумать и решить задачи.

Ориентировочные темы:

Бермудский треугольник… миф и реальность.

Египетские пирамиды – чудо света.

 Эйфелева башня - украшение Парижа.

VI. Рефлексия (подведение итогов)         

 

 

 

 

 

 

Урок № 9-10

 

Тема: Решение прикладных задач.

Цель урока: Создать условия для систематизации знаний и умений по теме «Решение треугольников».

Создать условия для выявления уровня овладения системой     знаний и умений, опытом творческой деятельности.

Создать условия для развития интеллекта, творческих способностей учащихся.

Создать условия для воспитания интереса к изучению математики.

Тип урока: Урок обобщения и систематизации знаний и умений.

 

Ход урока

1. Оргмомент.

    -Приветствие.

    -Проверка отсутствующих.

    -Установка “Внимание!”              

                       Математика интересна тогда, когда даёт пищу нашей 

                            изобретательности и способности к рассуждениям.  

                                                                                                     Д. Пойа.

     II. Целеполагание и мотивация.

    В детективной конторе (в связи с увеличением заказов) возникла потребность расширить штат. И конечно же владельцы вспомнили о нас, ведь мы давно учим геометрию, которая ум шлифует и формирует детективный стиль мышления.

    Мне поручено для выбора наилучшего из претендентов провести конкурс решения задач. Проведём его по теме «Решение треугольников»

Условия проведения конкурса:

предлагаем вам для решения задачи разной сложности;

решение каждой задачи оценивается определённым количеством баллов;

победит тот, кто наберёт наибольшее количество баллов.

 

III. Актуализация.

Сначала сделаем умственную зарядку.

(правильный ответ 0, 5 балла) 

1. На каких чертежах допущены ошибки в проставлении размеров?

 

 

 

                                                                                                             44

10             10       3                                                                       70°         

                                     5             5     100            8            19                                      

                                                                                                              25     

 

            10                     4                           6

 

 

2. Можно ли утверждать, что стороны треугольника пропорциональны синусам противолежащих углов. (Да, это теорема синусов)
3. Когда в треугольнике квадрат одной стороны равен неполному квадрату суммы двух других сторон. (Если сторона лежит против угла 120)
4. При каком условии основание равнобедренного треугольника больше боковой стороны? (если угол при вершине 60)

 Самопроверка с устным комментированием.

    IV. Систематизация и обобщение.

     А теперь переходим к серьёзным заданиям.

Задача 1. (1 балл) Два парохода начинают своё движение одновременно из Мариупольского порта и двигаются равномерно по прямым, пересекающимся под углом . Скорость первого парохода  км/ч, а второго -  км/ч. Вычислите, на каком расстоянии друг от друга будут находиться пароходы через  ч.

                                             С     BC² = AB² + AC² – 2AB AC  Cos

А                    at                          BC² = ()² + ()² - 2  Cos

                                                     BC =  √² + ² - 2  Cos

                   

                                         В

      bt

 

Ответ. BC =  √² + ² - 2  Cos

Задача 2.   (1,5 балла) На озере расположен небольшой остров А. Найдите расстояние от острова А до пункта В, находящегося на берегу. (Остров А принять за точку)

Задача 3. (1, 5 балла) Найти величину наибольшего угла треугольника, стороны которого равны 2м., 3м., 4м.

Задача 4.   (2 балла)  Для определения высоты шахтного террикона СD выбрали базис АВ=100м   и с помощью угломерного инструмента, высота которого АА₁=ВВ₁=1,4м, измерили углы ₁=25 и ₂=17. Используя результаты измерения, найдите высоту террикона.

                          С

                                                                                                                             

 

 

 

 

                                       ₁                  А1     ₂              В₁

                             _Е

                            _D

                                                                                                  _А                         В

 

 

V.Применение учебного материала в знакомой и новой учебных ситуациях.

Задачи каждый выбирает себе сам.

Задача 5.  (2, 5 балла) На сохранившейся карте старинного замка один угол оторван. Можно ли узнать длины неизвестных сторон, если известно, что замок имел форму трапеции?

 

 

 

 

3. 2

 

            30º                                                                                                                            

               4

 

 

 Похвалить того, кто догадался воспользоваться «принципом аналогии».  А иногда решать задачи помогает «динамический принцип». Этот принцип утверждает: не воспринимайте данные задачи как что-то неизменное. Например, если вам надо поймать преступника, то не забывайте, что он – живой человек и может вольно передвигаться в театре ваших боевых действий.

Задача 6.  (3 балла) Из двух пунктов А и В вышли одновременно два человека соответственно по направлениям АК и ВЕ, пересекающимся в точке С под углом 60º. Оба движутся равномерно со скоростью 2 км/ч и 3 км/ч соответственно. Через какое время с момента их выхода расстояние КЕ между ними станет равным первоначальному, если АС = 5км, ВС = 4 км?

Указания не должны влиять на творческую самостоятельность в решении проблем.   

Задача 7. (3, 5 балла) Силу, равную 23Н, требуется разложить на две составляющие, углы которых с направлением заданной силы равны 47º и 54º. Найдите величину каждой из этих сил.

В арсенале у детектива должно быть множество различных принципов, это и «принцип цели», и «принцип полного решения», который предусматривает использование всех данных задачи, и «принцип скальпеля», ведь иногда бывает полезно разрезать фигуру.

VI. Проверка уровня обученности.

      Взаимопроверка по готовым ответам.   

VII. Информация о домашнем задании.

Повторить теорию.  Решить № 15,16. А кто не хочет останавливаться на достигнутом и продолжить тренировку ума и сообразительности, тот попробует к следующему уроку составить и решить 2 – 3 задачи с детективным сюжетом.

VIII.  Рефлексия (подведение итогов).

  Мы рады поздравить победителя конкурса. У него есть все шансы стать сотрудником детективного агентства. А первая премия - 12 по геометрии за сегодняшний урок. На память о конкурсе каждый получает приз - оценку равную количеству баллов, заработанных на уроке.                                                                                                           

 

 

 

Урок № 11

 

Тема:  Решение треугольников

Цель урока: Создать условия для воспроизведения в памяти учащихся системы опорных знаний и умений.

Создать условия для проведения контроля умений и навыков                              учащихся по применению выученных теорем и следствий из них к                              решению задач.

Создать условия для развития творческого мышления, любознатель-

ности, интереса к математике.

Создать условия для воспитания таких черт характера, как стара-тельность, внимательность, коммуникабельность.

Тит урока: Урок актуализации знаний и умений.

Ход урока

I. Оргмомент.

• Приветствие
• Проверка отсутствующих
• Установка «Внимание!»

                                                   Математика - гимнастика ума

                                                                                 А.В.Суворов

     II. Целеполагание и мотивация.

     На протяжении десяти уроков мы с вами трудились, изучали теоремы косинусов и синусов, решали задачи, применяя данные теоремы, и сегодня мы с вами отдохнем – отправимся в путешествие в страну треугольников.

Статья 45 Конституции Украины закрепляет за нами такое право.

 

   III. Актуализация опорных знаний.

     Перед отъездом мы должны проверить, все ли прошли инструктаж для туристов, и готовы к путешествию.

 

Взаимоопрос. Теоремы синусов и косинусов.

 Итак, инструктаж вы прошли, и мы можем отправляться в путешествие. Но для приобретения билетов нужно правильно ответить на вопросы математического диктанта:

 

Вариант 1

1.Фигура, в которой сумма всех углов = 180˚.

2.Треугольник, один из углов которого больше суммы двух других.

3. Треугольник, сумма двух любых углов которого> 90˚

4. Отношение прилежащего катета к гипотенузе

5. Косинус угла в 45˚

6. Найдите градусную меру угла, если Cosα=0.65207

 

Вариант 2

1. Треугольник, сумма любых двух углов которого =120˚

2.Треугольник, один из углов которого равен сумме двух других.

3.Треугольник, сумма любых двух углов которого <120˚

4.Отношение противолежащего катета к гипотенузе

5.Синус угла в 60˚     

6.Найдите градусную меру угла, если Sinα=0.86116  

 

А теперь поменяйтесь работами и проверьте правильность своих ответов, оценив каждое значение. (На доске варианты ответов).

     Если вы правильно ответили на 4 вопрос, то вам не составит труда попасть в страну треугольников, ведь мы с вами нашли долготу и широту, на которой находится страна треугольников.

IV. Применение знаний.

     Итак, отправляемся в путь. Первая наша остановка «Теоремный полустанок».

     По готовым чертежам вы должны определить неизвестный элемент треугольника (устный счет). Вы можете заработать дополнительный балл.

  С

    х

   

        А               45˚     В        В

  6             х          3 

      А           60˚

        4   С

        А       

  х  12

      6      30˚

      С    В    х

          3

        45˚    30˚

 

Вы внимательно прослушали решение этих задач. А теперь вам необходимо оформить решение заданий (7-10 минут).

І вариант: № 1, № 3

П вариант: № 2, № 4

 

     А теперь проверьте правильность решения. На доске записаны решения.

      Отправимся дальше в путь. Вторая остановка «Созвездие треугольника АВС»

     «В предельно удаленном галактики конце

     Звенят тихонько звезды созвездья АВС….

     Их, судя по приметам, мы вычислить должны,

     И в АВС при этом найти две стороны».

 

        На ваших партах лежат треугольники, в которых вы должны измерить 2 стороны и угол (на треугольниках стоят вопросительные знаки) И по измеренным величинам определить третью сторону. За это задание вы можете заработать 4 балла. (сторону и градусную меру углов округляйте до целых величин)

         Практическая работа – 10 минут (4 вида треугольников)

         Итак, дальше в путь. Уже видна цель нашего путешествия. Третья остановка «Страна треугольников».

         Путешествуя в страну треугольников, вы увидели, что теоремы синусов и косинусов применяют не только для решения геометрических задач, но и для решения задач прикладного характера.

VII.  Информация о домашнем задании.

         Вам необходимо составить задачу прикладного характера, сделать рисунок и решить ее.

         Чтобы вам было легче справиться с заданием я приведу вам пример:

                                                   B

 

 

                                                   c      a              

                                                   120˚

                                    A

 

                                                        b

                                                                       C

 

На рисунке изображен подъемный кран, у которого стойка АВ=10 м, плечо АС=13м, а   ВАС = 120˚. Найти длину тяги ВС=?

     Выполнив правильно все виды работ, вы смогли набрать 11 баллов. Кто отвечал устно у доски заработал себе еще 1 дополнительный балл.

     Итак, максимум – 12 баллов.

VIII.  Рефлексия (подведение итогов урока)

     «Вот окончилось наше сказанье,

     Интересно вам было, иль нет?

     Наступает пора расставанья,

     С миром формул, задач и побед!».

 

 

 

Урок № 12

Тема. Контрольная работа по теме «Решение треугольников»

 

Цель урока. Создать условия для проверки уровня обученности, умений применять знания к применению задач; выявления пробелов в знаниях учащихся с целью их ликвидации на следующих уроках, определить методику коррекции учебной деятельности учащихся. Создать условия для развития навыков самостоятельной деятельности.

Создать условия для воспитания чувств ответственности за результаты своего труда.

Тип учебного занятия: Урок контроля и коррекции знаний и умений.

Ход урока

I. Оргмомент.

• Приветствие
• Проверка отсутствующих
• Установка «Внимание!»

                                      Работа – лучший способ наслаждения жизнью.

                                                                                                            Кант.

II. Целеполагание и мотивация.

III. Проведение контроля знаний.

VII.  Информация о домашнем задании.

         Составить задачу прикладного характера, сделать рисунок и решить ее или составить вопросы для викторины (с ответами).

VIII.  Рефлексия (подведение итогов урока)