Циліндр. Площа поверхні та об'єм циліндра

Міністерство освіти і науки України

Долинівська філія

КЗ «Гайворонський ліцей №1»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

План – конспект уроку

у 11 класі

на тему:

«Циліндр. Площа поверхні та об'єм циліндра.»

 

 

 

 

 

 

 

                                                                           Підготував:

                                                                                         вчитель математики

                                                                             Бондар М. В.

 

 

 

 

 

 

Тема уроку. Циліндр. Площа поверхні та об'єм циліндра.

Мета уроку: формування вмінь учнів знаходити площі поверхонь і об'єми циліндрів;

розвивати логічне мислення, увагу, вміння аналізувати,

обґрунтовувати та міркувати;

виховувати повагу до думки інших та відповідальне ставлення до результатів праці.

Тип уроку: комбінований.

Наочність і обладнання: таблиця «Початкові відомості стереометрії»;     моделі циліндрів.

Вимоги до рівня підготовки учнів: пояснюють, що таке циліндр та його елементи; зображують і знаходять на рисунку циліндр; записують й по­яснюють формули площі поверхні та об'єму циліндра; застосовують вивчений матеріал до розв'язування задач, у тому числі прикладного змісту.

 

Хід уроку

 

І. Перевірка домашнього завдання

Перевірити наявність виконаного домашнього завдання та від­повісти на запитання учнів, які виникли в них при розв'язуванні задач.

 

Розв'язання

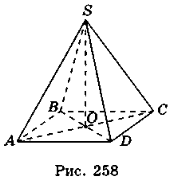
1. Нехай SABCD — правильна піраміда (рис. 258).

SA = SB = SC = SD = AB = BC = CD = AD = a.

S_п.п = S_осн + S_бічн = AB² + 4 ∙ 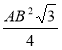= а² + а² =

= a²(1 + ).

Відповідь. а²(1 + ).

 

 

2) ABCD — ромб (рис. 259), AC = 8 см, BD = 6 cм, SO = 10 cм.

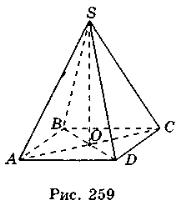
V = S_осн ∙ H = ∙ ∙ 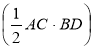SO = ∙ ∙ 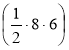10 = 80 (см³).

Відповідь. 80 см³.

 

3. SABCD — правильна піраміда (рис. 259). AC = 4 см, 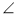ASO = 45°.

AO = AC = ∙ 4 = 2 (см). SO = AO = 2 (см).

S_осн = AC² = ∙ 4² = 8(см²). V = S_осн ∙ SO = ∙ 8 ∙ 2 = = 5 (см³).

Відповідь. 5см³.

 

Фронтальна бесіда

Визначте, які з наведених тверджень є правильними, а які — неправильними.

1. Кожне ребро трикутної піраміди дорівнює 6 см (рис. 260).

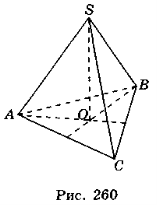
а) Периметр основи піраміди дорівнює 36 см.

б) Площа основи піраміди дорівнює 9 см².

в) Площа поверхні піраміди дорівнює 36 см².

г) Основа висоти піраміди не збігається з центром кола, впи­саного в основу піраміди.

2. В основі піраміди лежить квадрат зі стороною 10 см, бічні ребра піраміди дорівнюють 13 см (рис. 261).

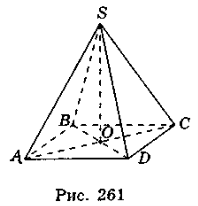
а) Периметр основи піраміди дорівнює 40 см.

б) Усі бічні ребра піраміди рівні.

в) Висота бічної грані піраміди, проведена з вершини пірамі­ди, дорівнює 11 см.

г) Площа бічної поверхні піраміди дорівнює 60 см².

  

3. В основі піраміди лежить рівнобедрений трикутник з бічною стороною l і кутом а при вершині (рис. 262). Висота піраміди дорівнює Н, основа висоти піраміди — центр кола, описаного навколо основи піраміди.

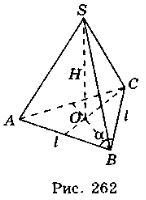
а) Площа основи піраміди дорівнює l²sinα.

б) Усі бічні ребра піраміди рівні.

в) Усі грані — рівнобедрені трикутники.

г) Об'єм піраміди дорівнює Нl²sinα.

 

II. Самостійна робота

Самостійну роботу навчального характеру можна провести за посібником [14], тест 18 «Многогранники».

 

III. Поетапне сприймання й усвідомлення нового матеріалу

Циліндр та його елементи

Прямим круговим циліндром називається тіло, утворене обер­танням прямокутника навколо його сторони.

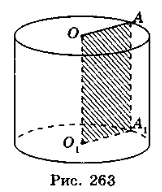
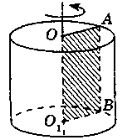
На рис. 263 зображено циліндр, утворений обертанням плос­кого прямокутника ОАВО₁ навколо прямої ОО₁ — осі циліндра.

Сторони ОА і O₁B описують рівні круги, які лежать у па­ралельних площинах і називаються основами циліндра. Радіуси кругів називаються радіусами циліндра.

Сторона АВ описує поверхню, яка називається бічною поверх­нею циліндра. Відрізки бічної поверхні, які паралельні й дорів­нюють АВ, називаються твірними циліндра.

Висотою циліндра називається відрізок, перпендикулярний до основ, циліндра, кінці якого належать основам. Висота цилін­дра дорівнює його твірній.

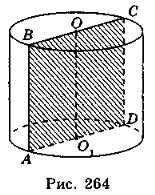
Осьовий переріз циліндра — прямокутник зі сторонами, що дорівнюють висоті циліндра й діаметру його основи. На рис. 264 прямокутник ABCD — осьовий переріз циліндра.

  

 

Завдання класу

1. Наведіть приклади побутових предметів, які мають форму циліндра.
2. Користуючись рис. 264, назвіть:

а) радіус циліндра; б) твірну циліндра.

3. Які властивості мають основи циліндра?
4. Які властивості мають твірні циліндра?
5. Із купи картону взяли аркуш і вирізали круг. Дістали циліндр з дуже малою висотою. Як практично визначити його висоту?
6. Кусок тонкого дроту можна вважати циліндром, у якого раді­ус дуже малий. Як практично визначити цей радіус?

 

Площа поверхні та об'єм циліндру

Поверхня циліндра складається з двох рівних основ і бічної поверхні.

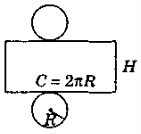
Якщо поверхню циліндра розрізати по колах основ і одній із твірних, а потім розгорнути на площині, то дістанемо розгортку циліндра (рис. 265). Вона складається з прямокутника, сторони якого дорівнюють довжині кола основ і висоті циліндра, і двох кругів, що є основами циліндра.

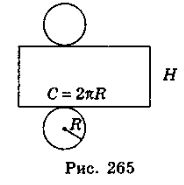
Площею бічної і повної поверхні циліндра називають площу розгортки бічної і повної поверхонь.

Тоді площа бічної поверхні S_бічн і площа повної поверхні S_цил визначаються формулами:

S_бічн = 2πRH,

S_цил = S_бічн + 2S_осн = 2πRH + 2πR² = 2πR(H + R),

де R, H — радіус і висота циліндра відповідно.

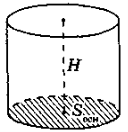
Об'єм циліндра дорівнює добутку площі його основи на висоту V = S_осн ∙ H.

Якщо радіус основи циліндра дорівнює R, а висота Н, то його об'єм

V = πR²H.

Розв'язання задач

1. Діаметр циліндра дорівнює 1 см, а висота дорівнює довжині кола основи. Знайдіть площу бічної поверхні циліндра.
2. Площа бічної поверхні циліндра дорівнює 15π см. Знайдіть площу осьового перерізу циліндра.
3. Осьовим перерізом циліндра є квадрат із стороною 8 см. Знай­діть бічну і повну поверхні циліндра.
4. Знайдіть об'єм тіла, утвореного при обертанні квадрата на­вколо його сторони, яка дорівнює 2 см.
5. Осьовий переріз циліндра — квадрат зі стороною 8 см. Знай­діть об'єм циліндра.
6. Знайдіть об'єм циліндра, якщо розгортка його бічної поверх­ні — квадрат зі стороною 8 см.

Учні складають конспект (зразок наведено у табл. 12).

Таблиця 12

Циліндр
	Прямим круговим циліндром назива­ється тіло, утворене обертанням пря­мокутника навколо його сторони. ОА, О1В — радіуси, АВ — твірна (ви­сота), O1O — вісь
	Площа поверхні циліндра Sцил = Sбічн + 2Sосн, де Sбічн = 2πRH, Sосн = πR2
	Об'єм циліндра V = Sосн ∙ H; V = πR2H

IV. Закріплення й осмислення нового матеріалу

Розв'язування задач

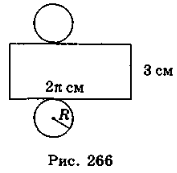
1. На рис. 266 зображено розгортку циліндра. За наведе­ними даними знайдіть площу і об'єм циліндра. (Відповідь. 8π см² і 3π см³.)
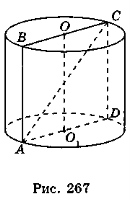
2. Діагональ АС осьового перерізу ABCD циліндра дорівнює 10 см, а його висота ОО₁ — 8 см (рис. 267). Знайдіть площу поверх­ні та об'єм циліндра. (Відповідь. 66π см² і 72π см .)

3. Діагональ осьового перерізу циліндра дорівнює d і утворює кут α з твірною циліндра. Знайдіть площу бічної поверхні та об'єм циліндра. (Відповідь. πd²sinαcosα,  .)

 

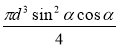V. Домашнє завдання

1. Вивчити формулу площі поверхні та об'єму циліндра.
2. Розв'язати задачу.

Об'єм циліндра — 8πсм³, а його висота — 2 см. Зна­йдіть діагональ осьового перерізу та площу бічної поверхні ци­ліндра.

 

VI. Підбиття підсумків уроку
Запитання до класу

1. Дайте означення циліндра.
2. Що таке висота циліндра? осьовий переріз циліндра?
3. Чому дорівнює площа бічної поверхні циліндра?
4. Чому дорівнює об'єм циліндра?
5.  

На рис. 268 зображено циліндр, радіус якого дорівнює 3 см, а висота – 4 см. Визначте, які з наведених тверджень є пра­вильними, а які – неправильними.

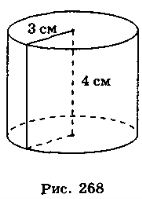
а) Довжина кола основи циліндра дорівнює 6π см.

б) Площа основи циліндра дорівнює 6π см .

в) Площа бічної поверхні циліндра дорівнює 2π см .

г) Об'єм циліндра дорівнює 24π см³.