Дана методична розробка рекомендована викладачам математики, учням для самостійного повторення теми «Куля», для підготовки до ДПА та ЗНО, а також систематизувати свої знання.
УПРАВЛІННЯ ОСВІТИ І НАУКИ
РІВНЕНСЬКОЇ ОБЛДЕРЖАДМІНІСТРАЦІЇ
ВИЩЕ ПРОФЕСІЙНЕ УЧИЛИЩЕ № 25 СМТ ДЕМИДІВКА
«КОМБІНАЦІЯ КУЛІ З ІНШИМИ ТІЛАМИ»
Автор: Волошин Світлана Володимирівна
викладач математики
І категорія
смт Демидівка
2019 р.
Комбінація кулі з іншими тілами. / Авт.: С.В.Волошин – ВПУ-25 смт Демидівка, 2013 р.
Дана методична розробка рекомендована викладачам математики, учням для самостійного повторення теми «Куля», для підготовки до ДПА та ЗНО, а також систематизувати свої знання.
Автор: С.В. Волошин – викладач математики ІІ категорії
«Погоджено»
на засідання предметної комісії
природничо-математичних дисциплін
протокол № 2 ,
від « 23 » вересня 2019 р.
Рекомендовано до друку навчально-методичною радою. Протокол № 3 від « 24 » вересня 2019 р.
При розв'язуванні задач на комбінацію кулі з многокутниками і тілами обертання потрібно встановити залежність між радіусом кулі і лінійними елементами тіл, що входять в комбінацію.
Успішне розв'язання таких задач потребує чіткої уяви про положення центра кулі в даній комбінації. Додатковий малюнок, в якому радіус кулі і пов'язані з ним елементи іншого тіла даються в натуральну величину (в розрізі), відповідають тій же меті.
Розглянемо основні види задач, розв'язання яких потребує від учнів 11-х класів попереднього визначення положення центра кулі.
І. Куля, описана навколо многогранника.
Куля називається описаною навколо многогранника, якщо всі вершини многогранника лежать на поверхні кулі. Звідси випливає, що всі вершини многогранника, вписаного в кулю, знаходяться на одній і тій самій відстані від центра кулі, що рівна радіусу кулі.
А. Пряма призма
Так як центр кулі рівновіддалений від вершини основи призми, то він знаходиться на перпендикулярі до площини основи, що проходить через центр кола, описаного навколо основи. Цей перпендикуляр і бічне ребро паралельні (два перпендикуляра до однієї площини), і визначають площину, в якій центр кулі повинен знаходитись на перпендикулярі до бічного ребра, що проходить через його середину. Дійсно, центр кулі повинен належати геометричному місцю точок, рівновіддалених від кінців бічного ребра.
Отже, центр кулі є серединою висоти призми, що проходить через центр кола, описаного навколо основи.
Наслідок:
1. Куля може бути описаною навколо прямої призми, якщо в основі останньої лежить многокутник, навколо якого можна описати коло; будь-який правильний многокутник (правильна призма); будь-який трикутник (трикутна пряма призма); чотирикутник, якщо суми протилежних кутів рівні - прямокутник, рівнобічна трапеція та інші.
2
Правильна чотирикутна призма (мал. 1)
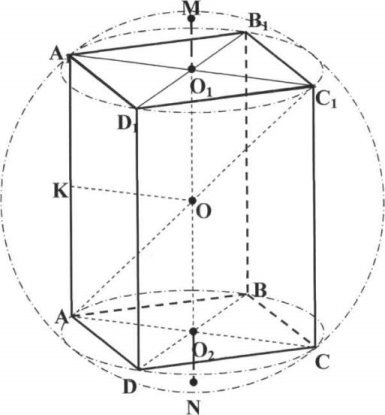
Правильна трикутна призма (мал. 2)
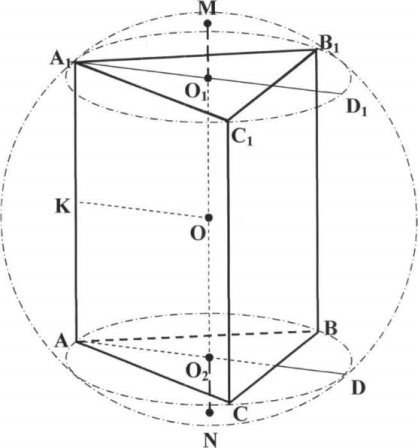
2. Центр кулі може знаходитись всередині призми, на бічній грані, зовні призми - в залежності від положення центра кола, описаного навколо основи.
В неправильній призмі слід попередньо знайти положення центра описаного навколо основи кола в відповідності з даними задачі.
Наприклад, розглянемо задачу:
Основою прямої призми є трикутник із сторонами 6 см, 8 см і 10 см. Висота призми 24 см. Знайти радіус описаної кулі.
В основі призми лежить прямокутний трикутник АВС (62+82=102). Центром кола, описаного навколо основи призми, є середина гіпотенузи АС -точка О2.
Таким чином, центр описаної навколо призми кулі лежить на середині висоти (О1О2), більшої бічної грані (АА1СС1) в точці О, яка ділить цю висоту пополам (мал. З).
(мал. 3)
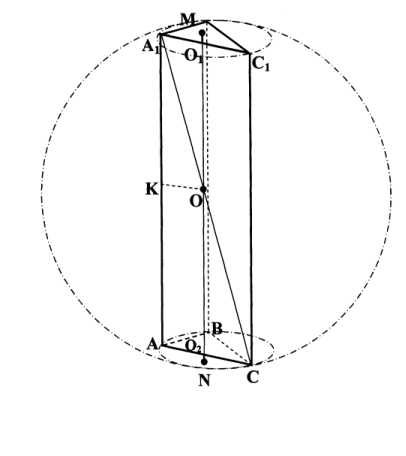
На малюнку А1С - діагональ прямокутника АА1С1С - є діаметром описаної кулі і А1О=ОС (точка О - центр симетрії прямокутника) - радіусом кулі.
![]()
![]()
![]()
Отже, радіус кулі дорівнює 13 см.
Б. Піраміда
Центр кулі, описаної навколо піраміди, лежить на перетині перпендикуляра до площини основи піраміди, що проходить через центр описаного навколо основи кола, і площини, перпендикулярної до бічного ребра, що проходить через середину останнього.
Кулю можна описати навколо піраміди, якщо можна описати коло навколо основи піраміди.
Центр описаної кулі може бути розташований всередині, на бічній грані, на основі і зовні піраміди. Точне знаходження положення центра кулі в кожному конкретному випадку робиться на основі аналізу даних.
В задачах на кулю, описаних навколо піраміди, що розв'язуються в школі, найчастіше зустрічаються піраміди, в яких перпендикуляр до площини основи, що проходить через центр описаного навколо основи кола і одне з бічних ребер лежать в одній площині. В цьому випадку центр описаної кулі лежить в тій же площині на перетині перпендикуляра до основи піраміди і перпендикуляра до бічного ребра, що проходить через середину ребра.
Розглянемо декілька випадків:
1. Правильна піраміда.
На малюнку 4 зображено правильну чотирикутну піраміду і правильну трикутну піраміду (мал. 5).
(мал. 4)
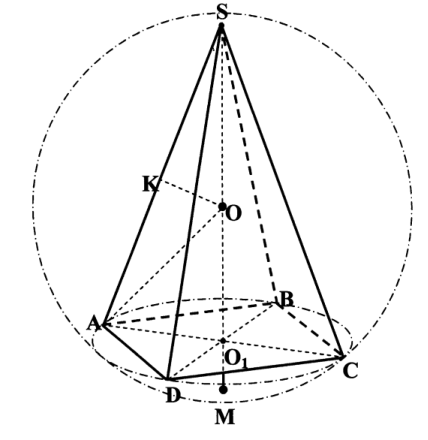
(мал. 5)
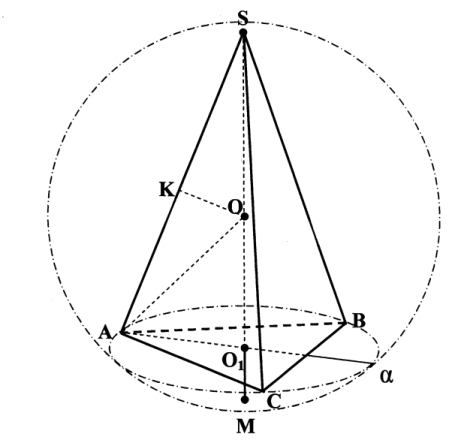
Якщо дано значення лінійних елементів і кутів, то потрібно знайти положення центра кулі відносно основи піраміди. Для цього потрібно розглянути прямокутний трикутник, утворений бічним ребром, висотою і радіусом основи піраміди.
(мал. 6)
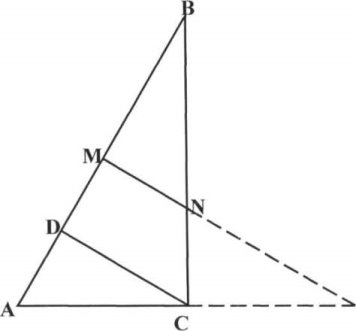
В прямокутному трикутнику перпендикуляр до гіпотенузи, проведений через її серединку перетинає більший катет і продовження меншого катета. Дійсно (мал.6), перпендикуляр CD, проведений з вершини прямого кута на гіпотенузу, перетинає її в точці D, яка ближче до вершини більшого кута (А). Звідси випливає, що якщо висота піраміди більша за радіус основи (або кут між бічним ребром і радіусом основи - більший з двох гострих), то центр кулі розташований всередині піраміди. Якщо ж вони рівні, то центр кулі лежить в основі піраміди. Якщо висота менша за радіус основи, то центр кулі знаходиться зовні піраміди, на продовження висоти.
Залежність між радіусом кулі і лінійними елементами піраміди встановлюється з трикутників АО1О або SКО. Потрібно мати на увазі, що ![]() (
(![]() - рівнобедрений).
- рівнобедрений).
2. Неправильна піраміда.
Тут, як було сказано, положення центра описаної кулі встановлюється аналізом заданих в умові задачі елементів. Для ілюстрації покажемо малюнки до задач.
Задача 1. Радіус кулі, описаної навколо піраміди SАВС, дорівнює m. Кут А основи піраміди дорівнює ![]() , кут С дорівнює
, кут С дорівнює ![]() , бічне ребро піраміди SА нахилено до основи під кутом
, бічне ребро піраміди SА нахилено до основи під кутом ![]() . Вершина піраміди (S) проектується в центр кола, описаного навколо основи.
. Вершина піраміди (S) проектується в центр кола, описаного навколо основи.
Знайти об'єм, якщо m=12,03, а=113°, ![]() =50°,
=50°, ![]() =37°.
=37°.
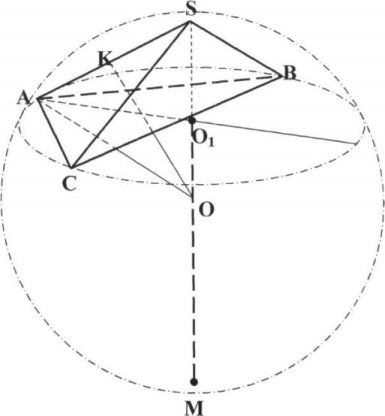
В основі піраміди АВС кут А - тупий (113°), тому центр описаного навколо основи кола О1, перпендикуляр до площини основи (SО1) і центр описаної кулі (О) лежать зовні піраміди (за бічною гранню).
Кут між бічним ребром (SА) і радіусом описаного навколо основи кола (АО1) менше 45° (![]() =37°), тому центр описаної кулі лежить нижче площини основи (мал.7).
=37°), тому центр описаної кулі лежить нижче площини основи (мал.7).
(мал. 7)
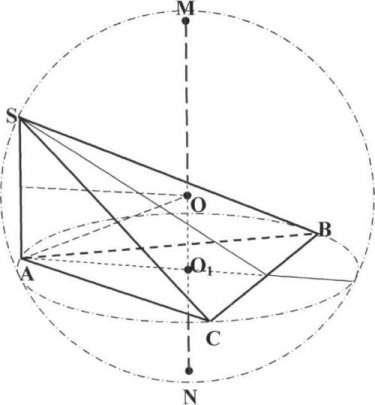
Задача 2.
Основою піраміди є правильний трикутник, сторона якого дорівнює 3дм. Одне з бічних ребер перпендикулярно до основи і дорівнює 2 дм. Знайти радіус описаної кулі (мал.8).
(мал. 8)
В. Зрізана піраміда.
Зупинимось на випадку правильної піраміди (мал.9). Центр описаної кулі лежить в точці перетину висоти зрізаної піраміди (О1О2) з перпендикуляром ОК до бічного ребра АА1, що лежить в площині АА1О1О2 і проходить через середину ребра А1А. Зв'язок між радіусом описаної кулі (АО=А1О), елементами основи піраміди і її висотою знаходиться з трикутників АОО2 і А1O1О.
Для неправильної піраміди деталі малюнка знаходяться відповідно з конкретними даними задачі.
(мал. 9)
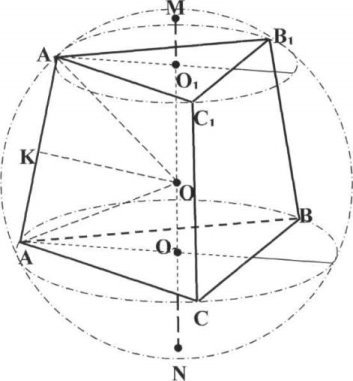
II. Куля, описана навколо круглих тіл.
Для знаходження положення центра кулі, описаної навколо циліндра, повного і зрізаного конусів, потрібно розглядати перпендикуляр до площини основи, що проходить через її центр (геометричне місце точок, рівновіддалених від точок кола) і перпендикуляр до твірної проведений через її середину в площині осьового перерізу.
В розв'язок задач тут нічого принципово нового не вноситься порівняно з розв'язуванням задач на кулю, описану навколо призми і піраміди. На малюнку можна обмежитись перерізом кулі - більшим кругом і вписаним в нього основним перерізом круглого тіла.
III. Куля, вписана в пряму призму.
Куля називається вписаною в многогранник, якщо всі грані многогранника дотикаються поверхні кулі.
10
Наслідок: Центр кулі віддалений від всіх граней описаного многогранника на одну і ту ж відстань, рівну радіусу кулі.
При встановленні положення центра кулі, вписаної в пряму призму, доцільно використати властивості бісектральної площини двогранного кута.
1. Бісектральна площина двогранного кута перетинає площину
лінійного кута по його бісектрисі.
2. Бісектральна площина двогранного кута є геометричним місцем
точок, рівновіддалених від граней двогранного кута.
В прямій призмі бісектральні площини двогранних кутів при бічних ребрах перетинають кути основи (лінійні кути цих двогранних кутів) по їх бісектрисам. Якщо бісектриси кутів основи перетинаються в одній точці (центрі вписаного круга), то бісектральні площини всіх двогранних кутів перетинаються по одній прямій, перпендикулярній до площини основи; всі точки цього перпендикуляра знаходяться від всіх бічних граней призми на рівній відстані.
Звідси випливає, що центр кулі, вписаної в пряму призму, є середина її висоти (куля дотикається до основ), проведеної через центр круга, вписаного в основу.
Наслідок: В пряму призму можна вписати кулю, якщо в її основу можна вписати круг і якщо висота призми рівна подвоєному радіусу цього круга.
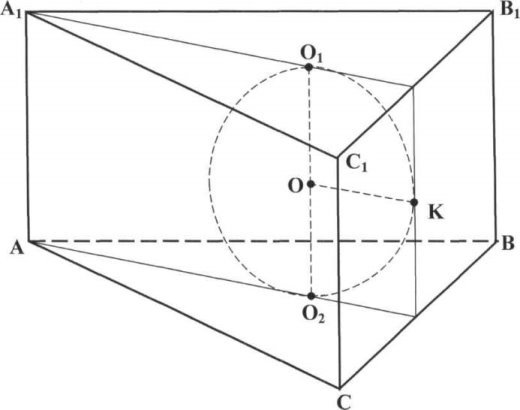
На мал. 10 в основі призми лежить ромб, на мал. 11 - куля вписана в правильну трикутну призму.
При розв'язуванні задач радіус кулі зв'язується з лінійними елементами призми або через висоту призми (дорівнює половині висоти), або через радіус вписаного в основу призми кола (дорівнює останньому).
11
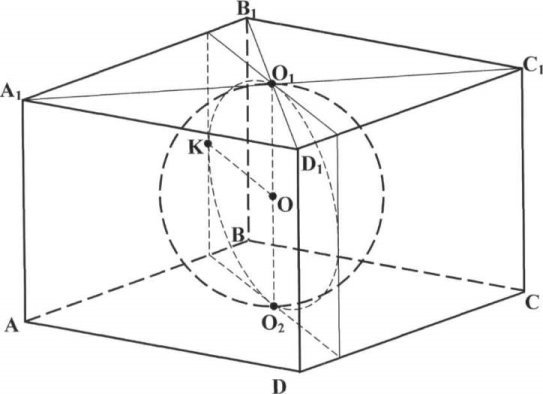
(мал. 10)
(мал. 11)
12
IV. Куля, вписана в піраміду та тіла обертання.
Розглянемо окремі випадки. А. Піраміда.
Розглянемо кулю, вписану в правильну трикутну піраміду (мал.12)., знайдемо положення центра. (мал. 12)
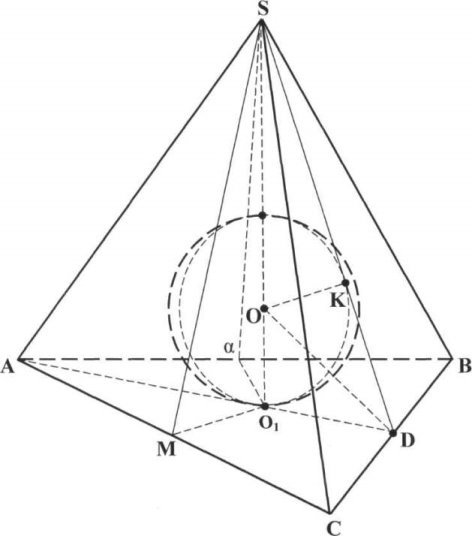
В прямокутний трикутник SО1D, утворений висотою піраміди (SО1) і апофемами бічної грані і основи, впишемо півкруг, центр якого лежить на перетині висоти піраміди з бісектрисою кута SDО1, а діаметр (NO1 лежить на висоті піраміди. При обертанні одержаного півкруга навколо діаметра NO1 одержимо кулю, вписану в піраміду.
13
Дійсно, точка D при обертанні ![]() буде лежати всередині
буде лежати всередині ![]() , за винятком тих випадків, коли SD співпадає з апофемами бічних граней. Таким чином, поверхня кулі дотикається до бічних граней і має з ними по єдиній спільній точці, що лежать на апофемах бічних граней. Поверхня кулі дотикається і до площини основи (перпендикулярної до радіуса кулі OO1) в точці О1.
, за винятком тих випадків, коли SD співпадає з апофемами бічних граней. Таким чином, поверхня кулі дотикається до бічних граней і має з ними по єдиній спільній точці, що лежать на апофемах бічних граней. Поверхня кулі дотикається і до площини основи (перпендикулярної до радіуса кулі OO1) в точці О1.
Отже, центр кулі, вписаної в правильну піраміду, лежить в точці перетину висоти піраміди з бісектрисою лінійного кута, утвореного апофемами бічної грані і основи. Зв'язок між радіусом кулі і лінійними елементами піраміди може бути встановлений кількома способами: на основі властивості бісектриси (ОD) внутрішнього кута трикутника; на основі залежності між дотичною (SК=SD-KD=SD-О1D), січною (SO1) і її зовнішньою частиною (SN=SО1-ОО1); із подібності трикутників SOK і SO1D і т.д.; для застосування тригонометрії можуть бути використані трикутники:
 Для неправильної піраміди, вершина якої проектується в центр вписаного круга, аналогічно встановлюється, що центр вписаної кулі лежить в точці перетину висоти піраміди і бісектриси лінійного кута, утвореного висотою бічної грані і радіусом вписаного в основу круга.
Для неправильної піраміди, вершина якої проектується в центр вписаного круга, аналогічно встановлюється, що центр вписаної кулі лежить в точці перетину висоти піраміди і бісектриси лінійного кута, утвореного висотою бічної грані і радіусом вписаного в основу круга.
Б. Зрізана піраміда.
На мал.13 зображено кулю, вписану в зрізану піраміду, бічні грані якої однаково нахилені до основи рівнобічної трапеції.
Обертанням прямокутної трапеції О1FMО2 і вписаного в неї півкруга О1NO2 навколо сторони трапеції О1О2 встановлюємо, що центр кулі, вписаної в зрізану піраміду, є середина висоти, що проходить через центр вписаного в основу круга.
14
(мал. 13)
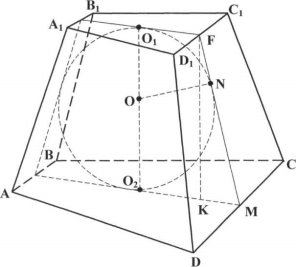
Куля дотикається до бічної грані з площиною, що проходить через висоту (О1О2) піраміди і радіус вписаного в основу кола, проведеної в точку дотику кола із стороною основи (по апофемі бічної грані для правильної піраміди).
Залежність між радіусом кулі і лінійними елементами піраміди встановлюється за допомогою трикутника FКМ, в якому катет FК - висота піраміди - дорівнює діаметру кулі, катет КМ є різницею радіусів вписаних в основи кіл.
В. Циліндри і конус.
Комбінацію циліндра і вписаної кулі можна розглядати як результат обертання прямокутника і вписаного в нього півкруга, діаметр якого співпадає з більшою стороною прямокутника, навколо діаметра півкруга; комбінацію конуса і вписаної в нього кулі - як результат обертання прямокутного трикутника і вписаного в нього півкруга.
Комбінацію зрізаного конуса і вписаної кулі можна розглядати як результат обертання прямокутної трапеції і вписаного в неї півкруга навколо бічної сторони трапеції, перпендикулярної до основи.
З такої точки зору знаходження положення центра вписаного кола і встановлення залежності між радіусом кулі і лінійними елементами круглих тіл не зустрічається труднощів.
15

про публікацію авторської розробки
Додати розробку
