Декілька задач "про ціни" (відсоткові розрахунки)

Декілька задач про ціни

 

Перед розв’язанням задач корисно проаналізувати деякі вправи про зміну цін і подати їх у вигляді схем, якими учням зручно буде користуватись при розв’язанні багатьох складних задач “про ціни ”.

 

Задача 1. Початкова ціна деякого товару або послуги становить 80 у.г.о. Знайти нову ціну, якщо:

а) відбулося підвищення на а%,

б) відбулося зниження на а%.                                                                                                   

Розв’язання:

а) P = P₀ + P₀· ^a  = P₀·(1+ ^a ) = P₀ ·(1+0,01·a);

                                                      100                   100

б) P = P₀ – P₀· ^a  = P₀·(1- ^a ) = P₀·(1-0,01·a).

                                                     100                  100

Зобразимо ці формули у вигляді схеми, показавши, що підвищення зображується стрілкою, що напрямлена від P₀ вгору, а зниження – стрілкою, напрямленою вниз від Р_0.

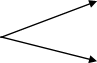 P₀ ·(1+0,01·а)                                                       а%

                          P_{0                                       а}% 

                                                   P₀ ·(1-0,01·а)

 

Задача 2. Початкова ціна деякого товару (послуги) становить P₀ у.г.о. Знайти кінцеву ціну, якщо:

а) відбулося підвищення ціни на а% з подальшим зниженням на b%;

б) відбулося зниження ціни на а% з подальшим підвищенням на b%  

 

 

Розв’язання:

а) P=P₀·(1+0,01·a) – ціна товару після першого підвищення, тоді за умови подальшого зниження одержимо: 

P*=P – P· ^b = P· (1-0,01·b) = P₀· (1+0,01·a)(1-0,01·b) 100

б) Р=P₀·(1-0,01·a) - ціна товару після зниження, тоді за умови подальшого підвищення одержимо:

P* = Р+ P· ^b  = P·(1+0,01·b) = P₀· (1-0,01·a)(1+0,01·b) 100

Процес знаходження кінцевої ціни можна зобразити у вигляді схеми, що відповідає розглянутим перетворенням вихідної суми Р_0.

        

                                 P₀· (1+0,01а)           b%

              а%                                                           P₀·(1+0,01a)(1-0,01b)

    P0                                                                                                                                                                               Р*

                                                                            P₀·(1-0,01a)(1+0,01b)                                            а%              

                                  P₀ · (1-0,01а)          b%

 

В фінансовій практиці для обчислення процентів найчастіше застосовують форми запису, що показані на схемах. Цей вигляд запису будемо називати стандартною формою.    

Розглянемо деякі приклади розв’язування задач.                                                        

 

Задача 3. Ціна на товар спочатку знизилась на 5%, а потім підвищилась на 5%.

Чи змінилась початкова ціна, якщо так, то на скільки процентів?                                       

Розв’язання: Складемо схему поступових змін початкової ціни:

        P₀                                                                 P₀ ·(1-5·0,01)·(1+5·0,01)=P*                       5%                              5%                        P₀ ·(1-5·0,01) 

 

Отже, P* = P₀·(1-5·0,01)(1+5·0,01) = P₀· (1-25·0,0001) = Р₀· (1-0,25·0,01)

Одержана стандартна форма запису свідчить, що початкова ціна знизилась на 0,25%

Задача 4. Ціна деякого товару підвищилась на 25%, а далі ще на 30%. Інший товар підвищився на 30% і став дорівнювати ціною першому товару. Яка початкова ціна першого товару, якщо другий до підвищення ціни коштував

1250 у.г.о.?

Розв’язання:  Нехай x у.г.о. – шукана початкова ціна першого товару.

Відобразимо дані перетворення цін на схемах

                                                         x· (1+25·0,01)(1+30·0,01)                    x· (1+25·0,01)       30%  x             25%    

 

            30 %          1250· (1+30·0,01)

1250 

 

Так як одержані ціни обох товарів за умовою рівні, то складемо і розв’яжемо рівняння: x· (1+25·0,01)(1+30·0,01) = 1250(1+30·0,01),

x·1,25 = 1250 x = 1000

Отже, початкова ціна першого товару становила 1000 у.г.о.

 

Задача 5. Деякий товар коштував 3150 у.г.о. Після двох послідовних знижень ціни його вартість становила 1512 у.г.о. Скільки коштував товар після першої знижки, якщо друга знижка на 20% більша за першу.

Розв’язання: Нехай x%- проценти першої знижки, тоді (x+20)%- процент другого зниження ціни. Складемо схему операцій з початковою ціною товару

        0            х%

                        3150· (1- x·0,01)      _х+20%

                                                              3150· (1-х·0,01)(1-( x+20)·0,01)

 

 

За умовою кінцева ціна становить 1512 у.г.о, що дозволить скласти рівняння. 3150·(1- x·0,01)(1- x·0,01-0,2) = 1512

(1-0,01·x)·(0,8-0,01·x) = 0,48

0,01·(100-x)·0,01·(80-x) = 0,48

Позбудемося дробів шляхом ділення обох частин рівняння на 0,0001:

(100- x)(80-x) = 4800

8000-180x+x² = 4800

Розв’яжемо квадратне рівняння x² –180x+3200 = 0, Отже, x₁=160; x₂ = 20.

Перший корінь не задовольняє умові задачі за змістом (продавець роздав би товар, приплативши ще 60%  його вартості).

Знайдемо значення виразу 3150· (1-x·0,01) за умови, що x=20, одержимо відповідь: ціна товару після першого зниження становитиме 2520 у.г.о.

 

Задача 6. Після трьох послідовних знижень на один і той же процент ціна товару знизилася із 125 до 64 у.г.о. На скільки процентів знижувалася ціна кожного разу?

Розв’язання: Нехай x% - процент знижки товару. Складемо схему операцій з початкової ціни 125 у.г.о.

 

125

        x%      125· (1-x·0,01)    x% 

                                               125·(1-x·0,01)(1-x·0,01)     x%  

                                                                                                

125·(1-x·0,01)²·(1-x·0,01) За умовою кінцева ціна становить 64 у.г.о., що дозволить скласти рівняння:

125· (1-x·0,01)³ = 64

(1-x·0,01)³ =   

( 1-x·0,01)³ = (  )³

Тоді 1– x·0,01 = ;  x·0,01 = 0,2; x = 20

Отже, ціна товару знижувалась на 20%.

Задача 7. В осінньо-зимовий період ціна на свіжі фрукти зростала тричі з 24 до 39,6 у.г.о. Друге підвищення на  10% більше за перше, а третє на 5% більше за друге. Знайти проценти зростання ціни на фрукти.

Розв’язання: Нехай х% - процент першого підвищення, тоді (х+10)% - друге підвищення ціни, а (х+15)% - третя знижка вартості товару. Складемо схему операцій з початкової ціни 24у.г.о.

            

24·(1+х·0,01)·(1+(х+10)·0,01)(1+(х+15)·0,01) 

                                                                   

                                    24· (1+х·0,01)(1+(х+10)·0,01)      _{х+15%                                   х+10%}               24(1+х·0,01)  

0 _х%

 

За умовою кінцева ціна складає 39,6 у.г.о. 

Розв’яжемо рівняння:

24·(1+0,01·х)·(1+(10+х)·0,01)·(1+(х+15)·0,01) = 39,6;

24·(1+0,01·х)·(1,1+0,01·х)·(1,15+0,01·х) = 39,6; 0,01·(100+х)·0,01·(110+х)·0,01·(115+х) = 1,65; (100+х)·(110+х)·(115+х) = 1650000.

Звідси одержимо рівняння виду х³+325х²+35150х-385000 = 0 Знайдемо корені за схемою Горнера:

	1	325	35150	-385000
10	1	335	38500	0

 

Квадратне рівняння х²+335х+38500 = 0 немає розв’язків в області R.

Тоді х = 10 є розв’язком даного рівняння. 

Отже, перша знижка становить 10%, друге зниження ціни складає 10+10 = 20%, а третє – 20+5 = 25%.

 

 

ВПРАВИ:

 

№1. Який процент щорічного прибутку давав банк, якщо внесок на рахунок становить 13000 у.г.о., а вкладник через два роки отримав 15730 у.г.о.

№2.  Ціна товару після двох послідовних знижень на один і той же відсоток зменшилась із 125 у.г.о. до 80 у.г.о. На скільки відсотків зменшувалась ціна кожного разу?

№3. В осінньо-зимовий період ціна на свіжі фрукти зростала тричі: на 10%, на 20% і на 25%. На скільки процентів зросла зимова ціна у порівнянні з літньою? №4. Власник магазину придбав товар по собівартості: 51,2 у.г.о. за одиницю товару. На шляху до прилавка ціна підвищувалася тричі на один і той же відсоток. Товар не користувався попитом, і комерсант надав розпорядження тричі зробити зниження на той же самий відсоток. В підсумку ціна виявилась рівною 21,6 у.г.о. за одиницю товару. Знайти процент зміни  ціни.

№5. На підприємстві виготовлення продукції зросло за рік на 4%, а наступного року підвищилося ще на 8%. Знайти середній річний приріст за ці два роки. №6.  В одній з газет повідомлялося, що в порівнянні з листопадом збільшилася   на 24,7% вартість  набору з 25 основних продуктів харчування і склала 391,3

у.г.о. Скільки  коштувала “харчова корзина ” (набір) у листопаді?

№7.  Один з видів термінових внесків передбачає нарахування 40% прибутку через рік зберігання грошей в банку. Якщо протягом визначеного терміну рахунок не скасовується, то договір автоматично продовжується на тих же умовах (пролонговується). Яка сума буде на рахунку через 3 роки при початковому внеску 10 000 у.г.о.?

№8. Ціна товару 150 грн. Знайдіть ціну товару після двох послідовних знижень, якщо перше було на 10%, а друге – на 5%.

№9. Ціну товару, що коштував 150 грн., спочатку зменшили на 20%, а потім нову ціну збільшили на 20%. Знайдіть ціну товару після двох переоцінок. №10. Ціну товару, що коштував 150 грн., спочатку збільшили на 20%, а потім нову ціну зменшили на 20%. Знайдіть ціну товару після двох переоцінок.

№11. Ціну товару, що коштував 100 грн., зменшили на 20%. На скільки відсотків треба підняти нову ціну, щоб отримати початкову?

№12. Ціну на товар знизили на 10%. На скільки відсотків треба підвищити нову ціну, щоб отримати початкову?

№13. Ціна краму спочатку знизилась на 10%, а потім ще раз на 10%. На скільки відсотків знизилась вона після двох переоцінок?

№14.  Ціна на автомобіль спочатку підвищилась на 20%, а потім знизилась на 20%. Як змінилась ціна на автомобіль після двох переоцінок?

№15.  Завод збільшив випуск продукції за перший рік на 20%, а за другий – на 25%. Як зріс випуск продукції на заводі за ці два роки?