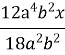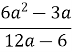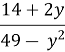Дії з раціональними виразами. Тотожні перетворення раціональних виразів

Тема: Дії з раціональними виразами. Тотожні перетворення раціональних виразів.

Мета:

• систематизувати та узагальнити знання учнів про раціональний вираз; удосконалити вміння застосовувати алгоритми множення і ділення, піднесення до степені, додавання та віднімання раціональних виразів при розв’язуванні вправ;  формувати розуміння важливості свідомого і міцного володіння системою математичних знань, умінь, навичок.
• формувати вміння аналізувати, контролювати та оцінювати результати своєї навчальної діяльності; сприяти самовихованню, прагнення до вдосконалення результатів діяльності та попередження помилки через неувагу.
• Розвивати алгоритмічну культуру учнів як здатність діяти за заданим алгоритмом.
• Виховувати в учнів інтерес до математики, активність, культуру математичних записів, вміння раціонально використовувати час.

Тип уроку: узагальнення та систематизація знань і вмінь учнів.

Обладнання та наочність: підручник «Алгебра 8 клас» (автор О.С. Істер); роздатковий маатеріал: опорний конспект, бланки з алгоритмом.

Девіз уроку: «Розкажи  - і я забуду;

Покажи – і я запам’ятаю;

Дай мені зробити – і я зрозумію»

Конфуцій

Хід уроку

І. Організаційна частина

- перевірка готовності учнів до уроку;

- привітання з учнями.

«Бажаю вам бути уважними, зібраними, бадьорими, доброзичливими. Розпочнімо урок з гарним настроєм і отримаємо від нього задоволення і гарні результати».

ІІ. Мотивація навчальної діяльності

А почнемо наший урок зі слів стародавнього мислителя Конфуція: «Розкажи  - і я забуду; покажи – і я запам’ятаю; дай мені зробити – і я зрозумію».

Ці слова стануть девізом нашого уроку, на якому ми пригадаємо матеріал з теми «Дії з раціональними виразами». Тобто пригадаємо дії додавання, віднімання, множення, піднесення до степені, ділення, скорочення. Щоб добре підготуватися до підсумкової контрольної роботи.

Народне прислів’я говорить: «Знання збирається по краплині, як вода в долині» тому і ми збиремо і нагадаємо все про раціональні вирази.

Повідомлення теми уроку «Дії з раціональними виразами та тотожні перетворення раціональних виразів» та мети уроку.

Мета уроку полягає в узагальненні знань способів перетворення раціональних ви разів та вмінь виконувати ці перетворення в комплекси.

• Розгорнути зошити і записати число та тему уроку.

ІІІ. Актуалізація опорних знань

Фронтальне опитування із частковим занесенням в опорний конспект учня.

• Щоб вміти перетворювати раціональні вирази в комплексі повторимо теорію із частковим записом в опорний конспект. У кожного на парті заготовлені бланки опорного конспекту з яким ми працюємо протягом уроку.

Питання

1. Які вирази називаються цілими, дробовими? (в опорний конспект виписати з дошки із завдання № 1, в цілі та дробові вирази)
2. Цілі і дробові вирази називаються … (рац.вир.)
3. На що треба звернути увагу перед перетворенням раціонального виразу?
4. Виписати в опорний конспект, з дошки завдання № 2,вирази, що є одночленами та многочленами.
5. Що називають допустимими значеннями змінної?
6. Виписати в опорний конспект, з дошки завдання № 1, допустимі значення змінної у дробових раціональних виразах.
7. Як додати (відняти) дроби з різними знаменниками (повторити за алгоритмом зведення дробів до спільного знаменника № 1).
8. Як виконати множення дробів (повторити за алгоритмом № 2).
9. К виконати ділення дробів (повторити за алгоритмом № 3).
10. Сформулювати правило піднесення дробу до степеня.
11. Як виконати скорочення дробів (повторити за алгоритмом № 4). Звернути увагу на дошку і повторити способи розкладання многочлена на множники).
12. Які дії з раціональними виразами ми вміємо виконувати (записати перелік дій в опорний конспект).

ІV. Застосування знань та вмінь (працюємо у класних зошитах)

1. Назвати найменший спільний знаменник

а) ;

б) ;

в)

2. Гра «Добери пару». Установіть відповідність між даними виразами та знайти тотожні рівні.

Наприклад: а) 2

3. Доведіть, що значення даного виразу не залежить від значень змінних, які до нього входять:

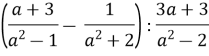
Фізкультхвилинка

Гра «Муха» (уявно муха сідає на ніс і учні намагаються очима поглянути на ніс, сіла на чоло – очима поглянути, глянути вниз, потім вона відлетіла і намагаються впіймати плескаючи обома руками над головою).

V. Самостійна робота (завдання с/р заготовлені в опорному конспекті. Учні працюють в опорному конспекті).

VI. Підсумок уроку.

На сьогоднішньому уроці ми з вами повторили та систематизували знання з теми «Дії з раціональними виразами. Тотожні перетворення раціональних виразів». Підсумок уроку проводимо за опорним конспектом.

VII. Оцінювання роботи на уроці.

Кожен з вас на сьогоднішньому уроці зробив свій внесок. За моїми спостереженнями:

• На високому рівні працювали - _____________________________________
• На достатньому рівні працювали - ___________________________________
• На середньому рівні працювали - ____________________________________

Але оцінку за урок я виставлю пізніше з урахуванням с/р. Загальний бал буде оголошено на початку наступного уроку.

VIIІ. Домашнє завдання

1. Повторити §1 - §7.
2. Використовуючи алгоритми виконати завдання с.37 (№6, №7, №5), с.38 (1, 2, 4, 5).

Опорний конспект

Алгоритм № 1 «Зведення дробів до спільного знаменника»

1. Знайти найпростіший спільний знаменник даних дробів.

1. Якщо чисельник і знаменник дробу є одночленами :

а) для числових множників знайти НСК

б) для степенів з однаковими основами вибираємо степінь з  найбільшим показником

2. Якщо чисельник і знаменник дробів многочлени, то для знаходження спільного знаменника, знаменник кожного дробу по можливості розкласти на множники.

2.            Знайти для кожного дробу додатковий множник. Для цього потрібно спільний знаменник поділити на знаменники даних дробів.
3. Помножити чисельник кожного дробу на його додатковий множник.
4. Записати дроби зі знайденими чисельниками та спільним знаменником. 

Алгоритм № 2 «Множення дробів»

І. Помножити окремо чисельник і окремо знаменники та записати перший добуток чисельником , а другий знаменником дробу

1. Якщо чисельник і знаменник є одночленами, то за правилом скорочення, скорочуємо отриманий дріб
2. Якщо чисельник і знаменник є многочленами, то їх розкладаємо на множники, а потім за правилом скорочуємо дріб

Алгоритм № 3 «Ділення дробів»

1. Щоб поділити один дріб на інший, потрібно перший дріб помножити на дріб, обернений до другого:

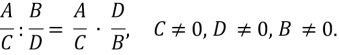
2. За правилом множення виконати множення дробів.

Алгоритм № 4 «Скорочення дробу, де чисельник і знаменник є раціональним виразом»

1. Якщо чисельник і знаменник дробу є одночленами то:

а)для числових множників підбирається

б)для степенів з однаковими основами підбираємо степінь з найменшим показником

2. Якщо чисельник і знаменник дробу многочлени, то перед скороченням їх потрібно розкласти на множники