Діагностична контрольна робота. Урок

Діагностична робота. Варіант 1

1. Запишіть 3 год 24 хв у хвилинах.

А)  324 хв ;        Б)   27 хв ;       В)   54 хв ;      Г)  204 хв .

1.2. Знайдіть різницю 

      А)  ;          Б)    ;          В)    ;           Г) .

1.3. Який з одночленів подано в стандартному вигляді?

      А)  ;      Б) ;    В) ;      Г) 

1.4. Знайдіть нулі функції 

     А)  5  і  3 ;        Б) -3 ;        В)  5 ;        Г)  3

1.5. Виконайте множення 

     А)    ;      Б)   ;     В) ;        Г) .

1.6. Внесіть множник під знак кореня  .

      А)    ;      Б) ;     В)    ;     Г)  

1.7. На рисунку зображено графік функції . Укажіть проміжок спадання функції.

  А) [ 2 ; 4] ;  Б) ;  В) ;  Г)   

1.8. Вкладник поклав до банку 1500 грн. Під який відсоток річних покладено гроші, якщо через рік на рахунку вкладника було 1725 грн.?

  А)  85% ;      Б) 115% ;      В) 25% ;      Г) 15% .

2.1. Розв’яжіть рівняння 

2.2. Побудуйте графіки функцій і . У бланк відповідей запишіть значення , при яких значення функції  менше за значення функції  .

2.3. Знайдіть знаменник геометричної прогресії , у якої .

3.1. Щоб ліквідувати запізнення на 24 хв, поїзд на перегоні завдовжки 180 км збільшив швидкість на 5 км/год порівняно зі швидкістю за розкладом. Якою є швидкість поїзда за розкладом?

3.2. Обчисліть , якщо

Діагностична робота. Варіант 2

1. Знайдіть значення виразу: 56 + 42 : 14 – 7

А)  52   Б) 50   В)  49   Г)  0

1.2. Чому дорівнює найменше спільне кратне чисел: 12 і 16?

      А)  2     Б)  4    В)  48    Г) 96

1.3. Яке з рівнянь є лінійним?

     А)      Б)       В)      Г)

1.4. Яка пара чисел є розв’язком системи: ?

      А)  (-1 ; -2)     Б)  (2 ; 1)      В)  (1 ; 2)     Г) (-1 ; 2)

1.5. Скоротіть дріб:

   А)     Б)       В)     Г)

1.6. Чому дорівнює сума коренів квадратного рівняння: ?

       А) 5    Б)  9     В)  -5     Г)   -9

1.7. Відомо, що . Яка з нерівностей хибна?

    А)     Б)       В)     Г)

1.8. Знайдіть суму нескінченої геометричної прогресії: -6 ; 1 ; …

     А)       Б)         В)       Г)  

2.1. Обчисліть значення виразу:

2.2. Знайдіть точки параболи, що є графіком функції , у яких абсциса й ордината – протилежні числа.

2.3. Розв’яжіть систему рівнянь:

3.1. Дві бригади, працюючи разом, зорали поле за 6 днів. За скільки днів може зорати поле кожна бригада, працюючи самостійно, якщо другій бригаді на це потрібно на 5 днів менше, ніж першій?

3.2. Обчисліть , якщо

Діагностична робота. Варіант 3

1. Знайдіть різницю: 16 год 26 хв – 9 год 52 хв

А) 7 год 26 хв    Б) 7 год 34 хв        В) 6 год 34 хв       Г) 6 год 26 хв

1.2. Знайдіть суму:            А)      Б)      В)      Г)

1.3. Який з виразів є одночленом?

     А)       Б)      В)       Г)

1.4. Областю визначення якої з функцій є будь-які значення ?

   А)      Б)      В)       Г)

1.5. Виконайте ділення:       А)      Б)    В)     Г)

1.6. Обчисліть значення виразу:

    А)      Б)  8      В)  2      Г)

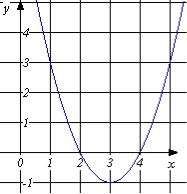
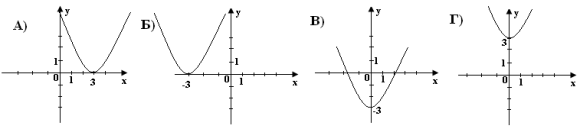1.7. На якому з графіків зображено графік функції

1.8. Яка ймовірність того, що при одному підкиданні грального кубика випаде кількість очок, що дорівнює парному числу?

    А) 1    Б)       В)      Г)

2.1. Розв’яжіть рівняння:

2.2. На прямій знайдіть точку, абсциса якої удвічі більша за ординату.

2.3. Знайдіть суму двадцяти перших членів арифметичної прогресії , якщо ,

3.1. Відстань між двома пристанями на річці дорівнює 45 км. Моторним човном шлях туди і назад можна подолати за 8 годин. Знайдіть власну швидкість човна, якщо швидкість течії 3 км/год.

3.2. Обчисліть , якщо

Діагностична робота. Варіант 4

1. Яке з чисел 3 ; 12 ; 14 є коренем рівняння: ?

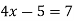А)  12      Б) жодного    В) 3    Г) 14

1.2. Виконайте множення:

    А)       Б)      В)      Г)

1.3. Подайте у вигляді многочлена вираз:

   А)     Б)     В)     Г)

1.4. Спростіть вираз:

    А)    Б)     В)     Г)

1.5. Обчисліть значення виразу:

    А) 14     Б) 6      В) 40      Г) 636

1.6. Виконайте ділення: 

А)         Б)      В)      Г)

1.7. Для якої нерівності число 1 є розв’язком?

  А)    Б)   В)   Г)

1.8. Вершина якої з парабол належить осі абсцис?

 А)      Б)     В)     Г)

2.1. Спростіть вираз:  

2.2. Один з коренів рівняння дорівнює 1,5 . Знайдіть і другий корінь рівняння.

2.3. У сплаві 60% міді, а решта – 200г – олово. Яка маса сплаву?

3.1. З міста в село, відстань між якими 450 км, виїхали одночасно два автомобілі. Один з них мав швидкість на 10 км/год більшу, ніж інший, і тому прибув у село на 30 хвилин швидше. Знайдіть швидкість кожного автомобіля.

3.2. Обчисліть