Діагностичні роботи за групами результатів з математики 6 клас НУШ (за програмою О. Істера)
Діагностичні роботи з математики 6 клас НУШ за модельною програмою О. Істер.
Також можна використати і для інших модельних програм.
Кожна робота містить по два рівнозначних варіанти.
Кожна робота поділена на три частини за групами результатів, оскільки кожен навчальний заклад вирішує як заповнювати журнал НУШ: в одній даті за діагностичну роботу оцінюють за кількома критеріями або в одній даті оцінка лише за одну групу результатів. Тому доцільно було б завдання діагностичних робіт частково виконати на самостійних роботах, уроках узагальнення. Оскільки, на мою думку, такий обсяг роботи неможливо оцінити за одну контрольну роботу, що також пропонують автори модельних програм В.Бевз та Н. Тарасенкова.
Оцінювання групи результатів 1 (ГР 1) Досліджує ситуації та створює математичні моделі - 2 завдання по 6 балів (в сумі 12 балів):
● наявність правильної відповіді – 1 бал;
● наявність математичної моделі (виразу, порядку дій) – 2 бали;
● правильне виконання дій – 1 бал;
● наявність пояснення до кожної дії – 1 бал;
● раціональність виконання моделі (якщо учень використав нестандартне рішення) – 1 бал.
Оцінювання групи результатів 2 (ГР 2) Розв`язує математичні задачі – 6 завдань (іноді 5-7) по 2 бали (в сумі 12 балів):
● наявність правильної відповіді – 1 бал;
● наявність запису виконаних дій – 1 бал.
Оцінювання групи результатів 3 (ГР 3) Інтерпретує та критично оцінює результати – 3 завдань (іноді 2-4) по 4 бали (в сумі 12 балів):
● наявність правильної відповіді – 1 бал;
● правильне виконання дій – 1 бал;
● наявність пояснення до кожної дії – 1 бал;
● наявність оцінки результатів – 1 бал.
Математика 6 клас
Діагностична робота № 1 з теми « Повторення вивченого у 5 класі»
Діагностична робота № 2 з теми «Звичайні дроби та дії першого ступеня з ними»
Діагностична робота № 3 з теми «Звичайні дроби та дії другого ступеня з ними»
Діагностична робота № 4 з теми «Відношення і пропорції»
Діагностична робота № 5 з теми «Відсоткові розрахунки. Коло. круг»
Діагностична робота № 6 з теми «Раціональні числа»
Діагностична робота № 7 з теми «Додавання і віднімання раціональних чисел»
Діагностична робота № 8 з теми «Множення раціональних чисел. Вирази»
Діагностична робота № 9 з теми «Ділення раціональних чисел. Рівняння»
Діагностична робота № 10 з теми «Координатна площина»
Підсумкова діагностична робота № 11
Діагностична робота № 1 з теми « Повторення вивченого у 5 класі»
Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. Виконайте дії : 
.
2. Розв’яжіть рівняння 
.
3. Туристи йшли три дні. За перший день вони пройшли 0,3 всього шляху, за другий день -
, а за третій решту 20 км. Знайдіть довжину всього шляху.
ГР-2 Виконати завдання
1. Порівняти:
1) 0,19….0,2;
2) 
;
3) 
;
4) 
.
2. Знайти периметр і площу прямокутника, сторони якого дорівнюють 5,5 м і 1,4 м.
3. Розв’язати рівняння:
1) 
;
2) 
;
3) 3,45х - 2,05х=3,15.
4. За малюнком знайти кут СОВ:
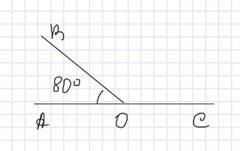
5. Обчислити:
)+1,8*0,5;
6. Знайти найбільше чотирицифрове число, що кратне числу 115.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Швидкість польоту птахів просто вражає: яструб малий може летіти зі
|
швидкістю 41,4 км/год, що на 8,3 м/год менше, ніж срібляста чайка. |
|
|
1) Яку швидкість може розвивати срібляста чайка?
|
|
|
2) У скільки разів швидкість стрижа більша за швидкість великої морської чайки, якщо стриж може летіти 120 км/год, а чайка – 50км/год?
|
|
|
3) Сокіл-сапсан може летіти зі швидкістю 140 км/год, а при пікіруванні розвиває швидкість в 7,78 разів більшу, ніж яструб малий. Обрахуйте, з якою швидкістю пікірує сокіл-сапсан. (відповідь округліть до одиниць) |
|
Діагностична робота № 1 з теми « Повторення вивченого у 5 класі»
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. Виконайте дії : 
.
2. Розв’яжіть рівняння 
.
3. Туристи йшли три дні. За перший день вони пройшли 0,4 всього шляху, за другий день -
, а за третій решту 8 км. Знайдіть довжину всього шляху.
ГР-2 Виконати завдання
1. Порівняти:
5) 0,29….0,3;
6) 
;
7) 
;
8) 
.
2. Знайти периметр і площу прямокутника, сторони якого дорівнюють 3,5 м і 2,4 м.
3. Розв’язати рівняння:
1) 
;
2) 
;
3) 0,11х + 0,08х=45,6.
4. За малюнком знайти кут СОВ:
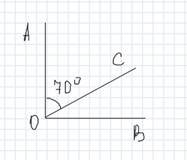
5.Обчислити:
)+2,5*0,4;
6. Знайти найменше п’ятицифрове число, що кратне числу 12.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
|
Смакуючи чізбургером, Артем прочитав на обгортці, що він містить 16 г білків, що становить 26% добової норми дорослого, 12 г жирів – 18% добової норми дорослого, а також вуглеводи і сіль. |
|
|
1) Скільки грамів солі в чізбургері, якщо її в 10 разів менше, ніж білків? |
|
|
2) Скільки грамів вуглеводів в чізбургері, якщо їх в 20 разів більше, ніж солі. |
|
|
3) Яка рекомендована добова норма споживання жирів для дорослої людини? Результат округліть до цілих. |
|
Діагностична робота № 2 з теми «Звичайні дроби та дії першого ступеня з ними»Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
3. Виконайте дії : 
.
4. Розв’яжіть рівняння 
.
3. Туристи йшли три дні. За перший день вони пройшли 0,3 всього шляху, за другий день -
, а за третій решту 20 км. Знайдіть довжину всього шляху.
ГР-2 Виконати завдання
1. Виконайте дії: а) 
; б) 
.
2. Скоротіть дріб: а) 
; б) 
; в) 
.
2 5 4 3
3. Порівняйте числа: а) 1 і ; б) 3 і 6 ; в) 5 і 8 .
4. Запишіть у вигляді звичайного дробу число: а) 0,5; б) 3,4.
1 9 7 3 9 14
5 1
5. Обчисліть: а) 7 42 ; б) 8 12 ; в) 14 21.
4 1 х 5 0,2 11
х
6. Розв'яжіть рівняння: а) 9 18 ; б) 6 3 . ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
1/3 сплаву складає золото, 4/9 — срібло, а решту — домішки.
1)Яку частину сплаву становлять домішки?
2) На скільки частин більше у сплаві срібла, ніж золота?
Діагностична робота № 2 з теми «Звичайні дроби та дії першого ступеня з ними»Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
5. Виконайте дії : 
.
6. Розв’яжіть рівняння 
.
3. Туристи йшли три дні. За перший день вони пройшли 0,3 всього шляху, за другий день -
, а за третій решту 20 км. Знайдіть довжину всього шляху.
ГР-2 Виконати завдання
1°. Виконайте дії: а) 
; б) 
.
2°. Скоротіть дріб: а) 
; б) 
; в) 
.
4 2 5 2
3°. Порівняйте числа: а) 1 і ; б) 9 і 3 ; в) 6 і 7 .
4*. Запишіть у вигляді звичайного дробу число: а) 0,2; б) 1,5.
2 8 5 5 5 7
5*. Обчисліть: а) 5 35 ; б) 7 14 ; в) 418 527 .
5 1 5 0,4 32
6*. Розв'яжіть рівняння: а) х 6 8; б) 8 х 5 .
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
7/12 сплаву складає олово, 5/24 — свинець, а решту домішки.
1) Яку частину сплаву складають домішки? (
2) На скільки частин більше у сплаві олова, ніж свинцю?
Діагностична робота № 3 з теми «Звичайні дроби та дії другого ступеня з ними»Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
У продуктовому магазині Галинка купила два види печива: одного — 2 5/6 кг по 42 грн за 1 кг; другого — 1 7/12 кг по 36 грн за 1 кг.
1) Як обчислити вартість першого виду печива?
2) Як обчислити вартість другого виду печива?
3) За який вид печива дівчинка заплатила більше й на скільки гривень більше?
4) Скільки всього кілограмів печива купила Галинка?
5) Скільки кілограмів печива залишилося в ящику масою 36 кг, якщо з нього відсипали 3/4 печива?
ГР-2 Виконати завдання
2 7 2 3
:
1°. Обчисліть: а) 5 9 ; б) 5 8 .
2°. Перетворіть у десятковий дріб: а) 
; б) 
.
3°. Знайдіть 
від числа 125.
4•. Розв'яжіть рівняння: а) 5х = 
; б) 
х = 16.
5•. Піджак коштує 80 грн. і складає 
вартості всього костюма. Скільки коштує костюм?
1 3 1
• 2 :3
6 . Виконайте дії: а) 7 14 ; б) 5 8 · 56. ГР-3Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
1/3 сплаву складає золото, 4/9 — срібло, а решту — домішки.
1) Скільки грамів золота міститься у 2,4 кг сплаву?
2) Яка маса сплаву (у кілограмах), якщо маса срібла в ньому — 600 г?
Діагностична робота № 3 з теми «Звичайні дроби та дії другого ступеня з ними»Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії Для фарбування паркана Оксанці потрібно купити два види фарби: однієї —
3 3/4 л по 72 грн за 1 л; другої — 7 5/8 л по 56 грн за 1 л.
1) Як обчислити вартість першого виду фарби?
2) Як обчислити вартість другого виду фарби?
3) За який вид фарби дівчинка заплатила більше й на скільки гривень більше?
4) Скільки всього літрів фарби купила Оксанка?
5) Скільки гривень потрібно заплатити майстрові за фарбування паркана, якщо він бере таку плату: 16 грн за 1 л використаної фарби?
ГР-2 Виконати завдання
5 3 5 9
:
1°. Обчисліть: а) 7 4 ; б) 7 13.
2°. Перетворіть у десятковий дріб: а) 
; б) 
.
3°. Знайдіть 
від числа 145.
4•. Розв'яжіть рівняння: а) 4х = 
; б) 
х = 49.
5•. Знайдіть ціну сервізу, якщо чайник коштує 96 грн. і складає 
вартості всього сервізу.
1 2 3
• 4 :7
6 . Виконайте дії: а) 3 9 ; б) 2 5 · 45. ГР-3Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
7/12 сплаву складає олово, 5/24 — свинець, а решту домішки.
1) Скільки грамів олова міститься в 8,4 кг сплаву?
24) Яка маса сплаву (у кілограмах), якщо маса свинцю в ньому — 1500 г?
Діагностична робота № 4 з теми «Відношення і пропорції»
Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
Відстань між Одесою та Львовом — 800 км.
1) Чому дорівнює відстань між цими містами на карті, масштаб якої 1 : 4 000 000?
2) Чому дорівнює відстань між Києвом та Вінницею, якщо відстань між цими містами на карті з масштабом 1 : 2 000 000 становить 13 см?
3) Який масштаб карти, якщо відстань між Полтавою та Львовом 880 км, а відстань між цими містами на карті становить 11 см .
4) За який час проїде відстань між Одесою та Львовом потяг, який за 1 год долає 100 км?
5) Якою має бути швидкість автомобіля, щоб проїхати цю відстань за 10 год?
ГР-2 Виконати завдання
7 3 1 5
1. Чи істинна пропорція 18 : 44 = 114 : 27 ?
2. Знайдіть невідомий член пропорції: 1,6 : х = 2,4 : 4,5.
3. У будинку 68 двохкімнатних квартир, що становить 17 % усіх квартир.
Скільки квартир у будинку?
3х 4 7
4. Розв'яжіть рівняння 6 = 8 .
5. 560 кг апельсинів розподілили між чотирма школами у відношенні 4:3:5:2. Скільки кілограмів апельсинів одержала кожна школа?
6. Дев'ять робітників виконують деяке завдання за 14 год. За який час виконають це завдання три робітники, якщо будуть працювати з тією ж самою продуктивністю праці?
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Завдання 3. Груші багаті біоактивними речовинами. У їхніх плодах містяться унікальні ефірні масла, біологічно активні речовини, які здатні підвищувати захисні сили організму.
Середня груша масою 200 г містить близько 20 г природного цукру.
1) Яку масу природного цукру в середньому містить 1 кг груш?
2) Скільки груш в середньому містять 500 г природного цукру?
Європейські вчені вважають, що денна норма вживання цукру для здорової дорослої людини становить близько 60 г.
3) Скільки груш потрібно з’їсти протягом доби одній людині, щоб поповнити денну норму цукру?
Вміст природного цукру в апельсинах становить близько 10 % їхньої маси.
4) Скільки апельсинів масою 200 г потрібно з’їсти протягом доби, щоб поповнити денну норму цукру?
5) Що краще з’їсти для поповнення денної норми: 2 груші, чи 2 апельсини, чи грушу й апельсин? Відповідь поясніть.
Діагностична робота № 4 з теми «Відношення і пропорції»
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
Відстань між Тернополем та Дніпром — 820 км.
1) Чому дорівнює відстань між цими містами на карті, масштаб якої 1 : 4 000 000?
2) Чому дорівнює відстань між Києвом та Харковим, якщо відстань між цими містами на карті з масштабом 1 : 2 000 000 становить 24,5 см?
3) Який масштаб карти, якщо відстань між Полтавою та Ужгородом 1150 км, а відстань між цими містами на карті становить 11,5 см .
4) За який час проїде відстань між Тернополем та Дніпром потяг, який за 1 год долає 80 км?
5) Якою має бути швидкість автомобіля, щоб проїхати цю відстань за 10 год?
ГР-2 Виконати завдання
1. Чи є істинною пропорція 5,4 : 3,4 = 8,1 : 5,1?
2. Знайдіть невідомий член пропорції: 
: 5 = х : 3
.
3. Авансом робітник одержав 84 гривні, що становить 12 % його за робітної плати.
Визначте зарплату робітника?
4х 5 8
4. Розв'яжіть рівняння 13 = 9 . 5. 1 600 кг бананів розподілили між чотирма дитсадками у відношенні: 4:7:3:2. Скільки кілограмів бананів одержав кожний дитсадок?
6. Чотири робітники виконують деяке завдання за 24 дні. За який час ви конають це завдання 32 робітники, працюючи з тією самою продуктивністю праці?
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Яблука відносять до дуже корисних продуктів. Вони містять різноманітні мікроелементи, вітаміни, невелику кількість аскорбінової кислоти, органічних кислот, досить багато пектину і клітковини. Середнє яблуко масою 150 г містить близько 15 г природного цукру.
1) Яку масу природного цукру в середньому містить 1 кг яблук?
2) Скільки яблук в середньому містять 300 г природного цукру?
Європейські вчені вважають, що денна норма вживання цукру для здорової дорослої людини становить близько 60 г.
3) Скільки яблук потрібно з’їсти протягом доби одній людині, щоб поповнити денну норму цукру?
Вміст природного цукру в бананах становить близько 12 % їхньої маси.
4) Скільки бананів масою 250 г потрібно з’їсти протягом доби, щоб поповнити денну норму цукру?
5) Що краще з’їсти для поповнення денної норми: 2 яблука, чи 2 банани , чи яблуко й банан? Відповідь поясніть.
Діагностична робота № 5 з теми «Відсоткові розрахунки. Коло. круг»
Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії Спортивний марафон — це забіг на дистанцію 42 км 195 м. У марафоні брали
участь люди різних національностей: українці — 42 % всіх учасників; поляки — 14 % усіх учасників; білоруси — 18 % усіх учасників. Крім того, до марафону долучились афроєвропейці (26 % усіх учасників). Загалом на забіг з’явилося 48,5 тис. учасників.
1) Скільки українців брало участь у спортивному марафоні?
2) Скільки поляків брало участь у спортивному марафоні?
3) Скільки білорусів брало участь у спортивному марафоні?
4) Скільки афроєвропейців брало участь у спортивному марафоні?
ГР-2 Виконати завдання
1. Маса однієї деталі дорівнює 20 г. Тоді маса 3 таких деталей...
а) утричі більша; б) утричі менша;
в) у 20 разів більша; г) удесятеро менша.
2. Автобус проїхав 120 км за 3 год, а 360 км — за 9 год. Тоді...,
а) 
; б) 
; в) 
.
3. Щоб знайти 26% від числа 84, потрібно...
а) 84 : 0,26; б) 84 · 0,26; в) 84 + 0,26; г) 84 – 0,26.
4. Якщо радіус кола дорівнює а см, то діаметр цього кола дорівнює...
а) 3а см; б) 4а см; в) а см; г) 2а см.
5. У формулі довжини кола C = πd d є його...
а) радіусом; б) центром; в) дугою; г) діаметром.
6. У формулі площі круга S = πR2 R є його...
а) діаметром; б) довжиною; в) центром; г) радіусом
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Діаметр колеса велосипеда дорівнює 58 см.
1) Який радіус цього колеса?
2) Чому дорівнює довжина дуги цього колеса?
3) Скільки повних обертів зробить колесо, якщо велосипед проїде 78,3 м (π ≈ 3)?
Колесо дитячого велосипеда для подолання відстані завдовжки 360 м зробило 400 обертів.
4) Чому дорівнює діаметр цього колеса (π ≈ 3)?
Діагностична робота № 5 з теми «Відсоткові розрахунки. Коло. круг»
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
Шкільний напівмарафон — це забіг на дистанцію 10 км. У такому марафоні взяли
участь учні школи. Із них: учні 6-го класу — 8 % усіх учасників; учні 7-го класу — 26 % усіх учасників; учні 8-го класу — 32 % всіх учасників; учні 9-го класу — 34 % всіх учасників. Загалом на забіг з’явилося 450 учнів.
1) Розрахуйте кількість учнів 6-го класу, які взяли участь у напівмарафоні .
2) Розрахуйте кількість учнів 7-го класу, які взяли участь у напівмарафоні .
3) Розрахуйте кількість учнів 8-го класу, які взяли участь у напівмарафоні .
4) Розрахуйте кількість учнів 9-го класу, які взяли участь у напівмарафоні .
ГР-2 Виконати завдання
1. Вартість двох зошитів дорівнює 60 к. Тоді вартість одного зошита є...
а) удвічі більшою; б) удвічі меншою;
в) у 60 разів більшою; г) удесятеро меншою.
2. За 2 кг яблук заплатили 4 грн., а за 3 кг таких же яблук — 6 грн. Тоді...
а) 
; б) 
; в) 
.
3. Щоб знайти 27% від числа 54, потрібно...
а) 54 : 0,27; б) 54 · 0,27; в) 54 + 0,27; г) 54 – 0,27.
4. Відстань від точки М, що лежить на колі, до центра О цього кола дорівнює 3 см. Точка В також лежить на цьому колі. Чому дорівнює довжина відрізка ВО?
а) 1 см; б) 3 см; в) 6 см; г) 1,5 см.
5. У формулі довжини кола С = 2πR R є його...
а) радіусом; б) центром; в) дугою; г) діаметром.
6. У формулі площі круга S = πR2 число π наближено дорівнює...
а) 3,41; б) 1,34; в) 4,13; г) 3,14.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Діаметр піци дорівнює 38 см.
1) Який радіус цієї піци?
2) Якої довжини буде сирний бортик цієї піци?
3) Яку площу потрібно змастити соусом?
4) Яку форму матиме шматочок піци?
Діагностична робота № 6 з теми «Раціональні числа»
Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
Оленка накреслила план вулиці Тараса Шевченка. Одній поділці на цьому плані відповідає 50 м.
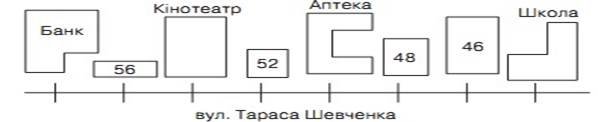
1) Що розміщено праворуч від аптеки на відстані 150 м?
2) Що розміщено на відстані 100 м від кінотеатру?
3) Що розміщено на відстані 50 м від будинку № 46?
ГР-2 Виконати завдання
1. Накресліть координатну пряму й позначте на ній числа 0; 1; 4; -6; -1,5; 2,5; -7.
2. Запишіть число, протилежне числу:
1)0,3; 2)-8; 3)-299; 4)8,9; 5)0.
3. Знайдіть модуль кожного із чисел: -3; -4,4; 22; 3,7; 0; -82. Запишіть відповідні рівності.
4. Позначте на координатній прямій числа, модуль яких дорівнює: 1)6; 2)5,5; 3)8.
5. Розв’яжіть рівняння:
1)|х| = 11; 2)|х| = 9; 3)|-х| = 7,8.
6. Порівняйте числа:
1)496 і -497; 3)0 і 83,5; 5)-0,0099 і -0,01; 2)-9,4 і -9,6; 4)-21і 0; 6)|-5| і |-б|.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Іринка взимку записувала показники термометра кожного ранку протягом тижня
(температуру визначала о 8 год ранку). У понеділок вона записала показник –6 °С. У вівторок і середу температура знижувалась на 2 °С щодня, а в четвер і п’ятницю — на 1 °С щодня. У суботу потеплішало, і температура підвищилася на 5 °С. У неділю температура не змінилася.
1) Який показник термометра Іринка записала у вівторок?
2) Який показник термометра дівчинка записала в середу?
3) Який показник термометра дівчинка записала в четвер?
4) Який показник термометра Іринка записала в п’ятницю?
5) Який показник термометра Іринка записала в суботу?
6) Який показник термометра дівчинка записала в неділю?
Діагностична робота № 6 з теми «Раціональні числа»
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
Світланка накреслила план вулиці Садової (мал. 6). Одній поділці на цьому плані відповідає 30 м.
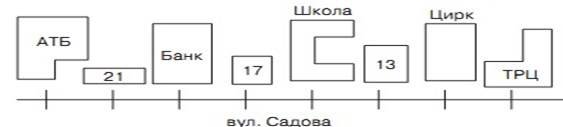
1) Що розміщено ліворуч від будинку № 17 на відстані 90 м?
2) Що розміщено на відстані 60 м від школи?
3) Що розміщено на відстані 30 м від цирку?
ГР-2 Виконати завдання
1. Накресліть координатну пряму й позначте на ній числа 0; -1; -4; 6; 1,5;- 2,5; 7.
2. Запишіть число, протилежне числу: 1) - 0,3; 2)8; 3)-200; 4)-81,9; 5)0.
3. Знайдіть модуль кожного із чисел: -31; -42,4; 22,4; -3,71; 0; -823. Запишіть відповідні рівності.
4. Позначте на координатній прямій числа, модуль яких дорівнює:1)7; 2)7,5; 3)8,5.
5. Розв’яжіть рівняння:
1)|х| = 10; 2)|х| = 8; 3)|-х| = 7,8.
6. Порівняйте числа:
1)-496 і -497; 3)0 і 8,5; 5)-0,0099 і -0,001; 2)-7,4 і -7,6; 4)-231і 0; 6)|-9| і |-б|.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Дані щодо зміни повітряного тиску записували з 19.11 по 27.11 (повітряний тиск
визначався о 8 год ранку). Дані з 19.11 по 22.11 подано в таблиці 6. Починаючи з 23.11 по 27.11 тиск щодня знижувався на 6 мм рт. ст.
1) Яким був повітряний тиск 20 .11, якщо 18 .11 він становив 747 мм рт . ст?
2) Яким був повітряний тиск 22 .11?
3) Як змінився тиск із 22 .11 по 23 .11, якщо з 21 .11 по 23 .11 тиск знизився на 15 мм рт . ст?
4) Який тиск було зафіксовано 27 .11?
5) Як змінився тиск з 19 .11 по 27 .11?
Діагностична робота № 7 з теми «Додавання і віднімання раціональних чисел» Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. Етиловий спирт замерзає при - 117°С, а точка його кипіння на 295°С вища. Яка точка кипіння етилового спирту?
2. Знайди різницю між найменшим цілим одноцифровим від’ємним числом і найбільшим цілим двоцифровим від’ємним числом.
3. Між Києвом і Одесою є місто Біла Церква, а між Білою Церквою і
Одесою – місто Умань. Від Києва до Умані – 212 км, від Одеси до Білої Церкви – 339 км, а від Умані до Білої Церкви – 130 км. Знайди відстань між
Одесою і Києвом. Запиши числову формулу розв’язання задачі.
ГР-2 Виконати завдання
1. Позначте на координатній прямій точки: A(3); B(-4); C(l,5); D(-l,5);
E(2,5). Які з позначених точок мають протилежні координати? (За одиничний відрізок візьміть довжину двох клітинок зошита.) 2. Порівняйте числа: а) -4,8 і 3,4; б) -2,4 і -2,7.
7 5 1 5
3 2
3. 
Обчисліть: а) 12 8 ; б) 9 6 .
4. Виконайте дії:
а) 2,8 + (-6,3) б) -5,4 + 9,2; в) -3,6 + (-4,9); г) -5,6 + 5,6;
д) 3,8 - 5,3; є) -18,6 - 3,6; ж) -5,6 - (-12,3); з) 0 - 3,8.
5. Розв'яжіть рівняння:
а) 7,16 + х = 4,25; б) 2,5 - (х - 3,08) = -1,07.
6. 
Обчисліть значення виразу, спростивши запис: 2 3 11 5 3 4 2
а) 7 + (-8) - (12) - (-7) + 13-20; б) 4 2 6 8 3 ;
в) -0,96 + (-5,37 + 1,03) - (6,03 - 2,7).
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
Джмелі витримують температуру до -7,80С, оси – вищу від цієї на 1,40С, а бджоли – нижчу від цієї на 1,40С. Яку температуру витримують бджоли й оси?
Діагностична робота № 7 з теми «Додавання і віднімання раціональних чисел» Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. Метиловий спирт кипить при +64°С, а точка його замерзання на 158°С нижча. Яка точка замерзання метилового спирту?
2. Знайди різницю між найменшим непарним двоцифровим додатним числом і найменшим парним одноцифровим від’ємним числом.
3. Користуючись малюнком, знайди відстань між пунктом С і D.
Запиши формулу для знаходження відстані CD.
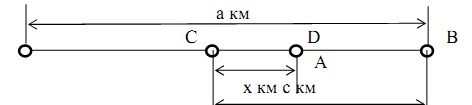
ГР-2 Виконати завдання
1. Позначте на координатній прямій точки: А(2); B(-3); С(2,5); D(-2,5); E(-4). Які з позначених точок мають протилежні координати? (За одиничний відрізок візьміть довжину двох клітинок зошита.)
2. Порівняйте числа: а) 4,1 і -7,1; б) -5,02 і -5,6.
6 9 5 5
5 3
3. 
Обчисліть: а) 7 14 ; б) 8 6 .
4. Виконайте дії:
а) -8,4 + 6,8 б) 13,3 + (-8,8); в) -3,8 + (-7,6); г) 4,8 + (-4,8);
д) 4,8 - 5,4; є) -15,7 - 6,5; ж) -3,2 - (-14,1); з) 0 - (-3,5).
5. Розв'яжіть рівняння: а) 8,97 + х = 4,15; б) -3,2 + (2,5 – х) = -2,7.
6. 
Обчисліть значення виразу: 3 5 1
132155
а) 12 + (-20) - (-11) + 18 - (-6) -10; б) 12 3 8 4 6 ;
в) -(8,31 + 6,27) + (-8,44 + 31,67) - 0,15.
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
У касі було 5000 грн. Упродовж дня касир кілька разів видавав і приймав гроші, роблячи записи: -120грн, -300грн, 460грн, 530грн, -1270грн, -650грн. Скільки грошей залишилося в касі на прикінці дня?
Діагностична робота № 8 з теми «Множення раціональних чисел. Вирази»
Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
У бабусі в господарстві є 24 курки з курчатами, причому курок — у 5 разів менше, ніж курчат.
1) Скільки курок у бабусі?
2) Скільки курчат у бабусі?
У білої курки на 2 курчати більше, ніж у чорної курки. У двох рудих курок курчат порівну, проте на 1 курча менше, ніж у білої курки.
3) Скільки курчат у чорної курки?
4) Скільки курчат у рудої курки?
5) Скільки курчат у білої курки?
ГР-2 Виконати завдання
1. Який результат дістанемо, застосувавши розподільний закон множення для обчислення виразу (0,03 + 2,5) · 0,4?
2. Який вираз дістанемо, розкривши дужки в добутку -5р(-х + 2у – 3k)?
3. Який вираз дістанемо, спростивши вираз 4с(3а – 2) – 6а(2с + 1)? 4. Обчисліть значення виразу 5·(5p – 4х) – 4·(х – 2p), якщо p = -2; х = 2.
5. Укажіть корінь рівняння -5·(у – 2) + 3(2 – у) = 0:
6. Обчисліть найзручнішим способом: -0,2 · 3,8 - 3, 7 · (-0,2);
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням У таблицях показано, як Дмитро й Наталка розв’язували приклади.
1) Хто з дітей правильно виконав дії ?
2) Хто з дітей правильно виконав дії ?
Діагностична робота № 8 з теми «Множення раціональних чисел. Вирази»
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
Чотири котики — Сніжок, Пушок, Мурчик і Нявчик — полювали на мишей. Сніжок уполював деяку кількість мишей, Пушок — на 2 миші менше від Сніжка, Мурчик — удвічі більше за Сніжка, а Нявчик — утричі більше за Пушка. Разом вони вполювали 48 мишей.
1) Скільки мишей уполював Сніжок?
2) Скільки мишей уполював Пушок?
3) Скільки мишей уполював Мурчик?
4) Скільки мишей уполював Нявчик?
ГР-2 Виконати завдання
1. Яке з поданих чисел дістанемо, застосувавши розподільний закон множення до виразу (12,5 + 0,1) · 0,8?
2. Який вираз дістанемо, розкривши дужки в добутку -2k(3а – 5b – 2с)?
3 Який вираз дістанемо, спростивши вираз 5p · (-3 + k) – k · (5p – 1)?
4. Обчисліть значення виразу (2х - 3у) – 2·(5х - 2у), якщо х = -1, у = 1?
5. Знайдіть корінь рівняння (х – 1) – 2(1 – х) = 12:
2 2 49 6 . Обчисліть найзручнішим способом: 3 9 .
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
У таблицях показано, як Дмитро й Наталка розв’язували приклади.
1) Хто з дітей правильно виконав дії ?
2) Хто з дітей правильно виконав дії ?
Діагностична робота № 9 з теми «Ділення раціональних чисел. Рівняння»
Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. -Маша купила на 2 ручки більше, ніж Сашко, а разом вони купили 10 ручок. По скільки ручок купили Маша і Сашко? (Саша – 4, Маша – 6) 97 2.- . В одному бідоні було в 3 рази більше молока, ніж у другому. Коли з першого бідона відлили 12 л. молока, а в другий долили 14 л, в обох бідонах молока стало порівно. Скільки літрів молока було в другому бідоні спочатку?
3. - Розв'яжіть рівняння:
9*(4-2х)=5*(3-4х)+4. (-8,5)
ГР-2 Виконати завдання
4 5 11
1) Виконайте ділення: -5,5 : 5; 10,32 : (-2,5); 7 : 14 .
15,64:4 7,12 2
2) Знайдіть значення виразу 5 .
1
3) Знайдіть значення виразу (а2 + 2b3) : 2+ 0,5, якщо а = -3, b = -.
4) Розв'яжіть рівняння: а) -9х = 36; -1,8 : х = -5,4;
7 11 13 51 x 1 3x 31
б) 12 x + 12 = 18 ; в) 63 5 3 .
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
За перший тиждень після відкриття молокозавод випустив 40 000 порцій морозива.
Потягом наступних трьох тижнів кількість морозива, що випускали, збільшувалась у
2 рази щотижня
На молокозаводі морозиво фасують в упаковки по 100 г (мала упаковка), по 500 г (середня упаковка) і по 1 кг (велика упаковка). Відомо, що малих упаковок випускають у 5 разів більше, ніж середніх, а середніх — у 2 рази менше, ніж великих.
1) Скільки порцій морозива в малих упаковках випустили на заводі за перший тиждень роботи?
2). Який відсоток морозива, що випускають на молокозаводі за тиждень, становлять порції: 1) у малих упаковках; 2) у середніх упаковках; 3) у великих упаковках?
3) Ціна морозива в малій упаковці становить 5 грн, у середній — 20 грн, а у великій — 35 грн. Яке морозиво вигідніше купувати з огляду на вартість 1 г морозива? Відповідь поясніть.
Діагностична робота № 9 з теми «Ділення раціональних чисел. Рівняння»
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. Петро зібрав у тричі більше грибів, ніж Дмитрик. Разом вони зібрали 30 грибів. Скільки грибів зібрав кожний? (Дмитрик -5, Петро – 15).
2. На одній овочевій базі зберігалося в 4 рази більше буряків, ніж на другій. Після того як з першої бази вивезли 7 т. буряків, а на другу завезли 17 т., буряків на цих базах стало порівну. Скільки буряків було на першій базі спочатку?
3. Розв'яжіть рівняння:
4*(х-16,5)=6*(3х-2)-2х. (-4,5)
ГР-2 Виконати завдання
21 : 4 1 1) Виконайте ділення: 8,4 : (-0,7); -8,88 : 2,4; 8 4 .
48 :3,9816,3
2) Знайдіть значення виразу 5 .
3) Знайдіть значення виразу (5m3 – 2mk) : m2, якщо m = -
; k = 0,75.
4) Розв'яжіть рівняння:
7 t 11 13 3 1 x 1 3x 111
a) -8x = 72; -1,7 : x = -5,1; б) 9 12 18 ; в) 4 6 3 2 .
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
За перший тиждень після відкриття молокозавод випустив 50 000 упаковок йогурту. Протягом наступних трьох тижнів кількість йогурту, що випускали, збільшувалась в 1,5 рази щотижня.
На молокозаводі йогурт фасують в упаковки по 125 г (мала упаковка), по 250 г (середня упаковка) і по 500 г (велика упаковка). Відомо, що малих упаковок випускають у 2 рази більше, ніж середніх, а середніх — у 3 рази більше, ніж великих.
1) Скільки порцій йогурту в малих упаковках випустили на заводі за перший тиждень роботи?
2) Який відсоток йогурту, що випускають на молокозаводі за тиждень, становлять порції: 1) у малих упаковках; 2) у середніх упаковках; 3) у великих упаковках?
3) Ціна йогурту в малій упаковці становить 8 грн, у середній — 15 грн а у великій — 30 грн.
9) Який йогурт вигідніше купувати з огляду на вартість 1 г йогурту? Відповідь поясніть.
Діагностична робота № 10 з теми «Координатна площина»
Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. Побудуйте на координатній площині ΔABC, якщо A(2; 1); B(-4; 1); C(2; -5).
а) Знайдіть координати точок перетину сторін трикутника з осями координат.
б) Через точку А проведіть пряму, паралельну стороні ВС, і пряму, перпендикулярну стороні ВС.
2. 
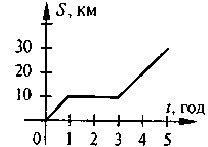На рисунку зображено графік руху велосипедиста. За графіком визначте:
а) Яку відстань проїхав велосипедист за увесь час руху?
б) Упродовж якого часу велосипедист відпочивав?
в) Яку відстань подолав велосипедист після зупинки?
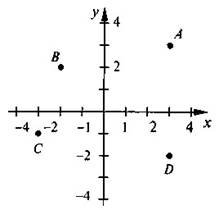
ГР-2 Виконати завдання
1. Знайдіть координати точок, зображених на рисунку.
2. Позначте на координатній площині точки A(3; -2); B(-
1;0
4; 3); С(0; -7); D 2 .
3. Через точку М, що лежить поза прямою а, проведіть пряму:
а) паралельну прямій а;
б) перпендикулярну прямій а.
4. Побудуйте на координатній площині ΔABC, якщо A(2; 1); B(-4; 1); C(2; -5).
а) Знайдіть координати точок перетину сторін трикутника з осями
координат.
б) Через точку А проведіть пряму, паралельну
стороні ВС, і пряму, перпендикулярну стороні ВС.
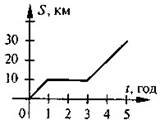
5. На рисунку зображено графік руху велосипедиста. За графіком визначте:
а) Яку відстань проїхав велосипедист за увесь час руху?
б) Упродовж якого часу велосипедист відпочивав?
в) Яку відстань подолав велосипедист після зупинки?
6. Побудуйте графік зміни температури повітря протягом 12 годин, використавши дані таблиці:
|
Час, t (год) |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
|
Температура, °С |
-1 |
0 |
1 |
2 |
3 |
5 |
7 |
|
|
|
|
|
|
|
|
|
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням
В автосалоні продають автомобілі трьох кольорів. Продаж автомобілів кожного кольору обліковують окремо. У таблиці наведено дані щодо кількості автомобілів білого й синього кольорів, проданих з 1.03 по 5.03. Дані про кількість автомобілів червоного кольору, проданих у цей же період, наведено на малюнку
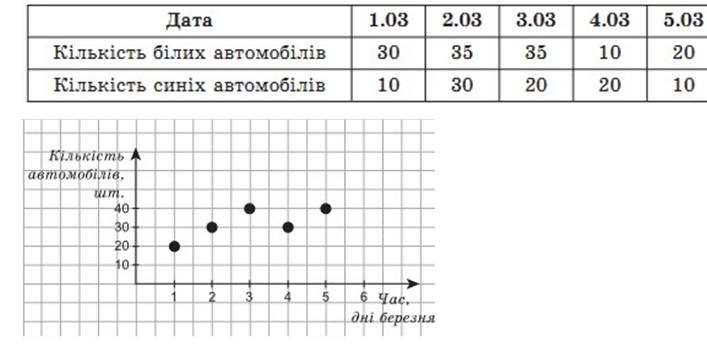
1) Заповніть таблицю
2) Автомобілі якого кольору мали найбільший попит за ці дні?
3) На скільки більше було продано за перші два дні автомобілів білого кольору, ніж автомобілів синього кольору?
4) Побудуйте графік продажу автомобілів усіх трьох кольорів залежно від дати з 1.03 по 5.03.
Діагностична робота № 10 з теми «Координатна площина»
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1.- Побудуйте на координатній площині ΔMNP так, що M(3; 0); N(-2; -3); Р(-2; 1).
а) Знайдіть координати точок перетину сторін трикутника з осями координат.
б) Через точку Р проведіть пряму, паралельну стороні MN, і пряму, ерпендикулярну стороні MN.
2.- 5. На рисунку зображено графік руху пішохода. Користуючись цим графіком,
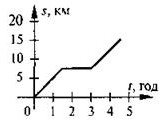відшукайте відповіді на запитання: а) Яку відстань подолав пішохід до зупинки?
б) За який час пішохід подолав відстань у 10 км?
в) Упродовж якого часу пішохід відпочивав? ГР-2 Виконати завдання
1. 
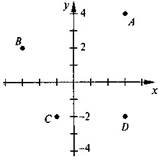Знайдіть координати точок, зображених на рисунку:
2. Позначте на координатній площині точки C(3; 5); D(-3; 4); 0; 1
E(2; 0);F 2 .
3. Через точку А, що лежить поза прямою с, проведіть пряму:
а) паралельну с;
б) перпендикулярну с.
4. Побудуйте на координатній площині ΔMNP так, що M(3; 0); N(-2; -3); Р(-2; 1).
а) Знайдіть координати точок перетину сторін трикутника з осями координат.
б) Через точку Р проведіть пряму, паралельну стороні MN, і пряму,
перпендикулярну стороні MN.
5. На рисунку зображено графік руху пішохода. Користуючись цим графіком, відшукайте відповіді на запитання:
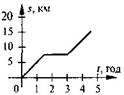а) Яку відстань подолав пішохід до зупинки?
б) За який час пішохід подолав відстань у 10 км?
в) Упродовж якого часу пішохід відпочивав?
6. Побудуйте графік зміни температури повітря протягом 12 годин, використавши дані таблиці:
|
Час, t (год) |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
|
Температура, t°С |
3 |
5 |
7 |
6 |
4 |
3 |
0 |
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням В автосалоні продають автомобілі трьох кольорів. Продаж автомобілів кожного кольору обліковують окремо. У таблиці наведено дані щодо кількості автомобілів білого й синього кольорів, проданих з 1.03 по 5.03. Дані про кількість автомобілів червоного кольору, проданих у цей же період, наведено на малюнку
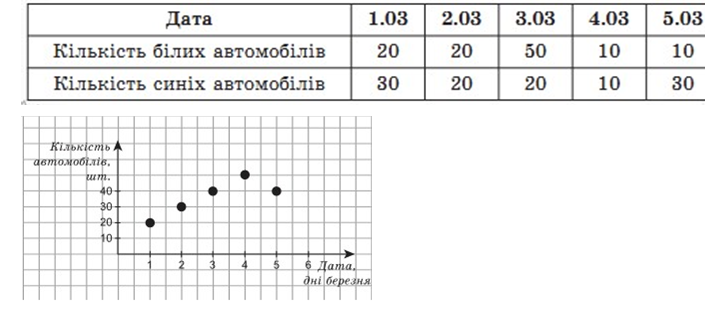
1) Заповніть таблицю
2) Автомобілі якого кольору мали найбільший попит за ці дні?
3) На скільки більше було продано за перші два дні автомобілів синього кольору, ніж автомобілів білого кольору?
4) Побудуйте графік продажу автомобілів усіх трьох кольорів залежно від дати з 1.03 по 5.03
Підсумкова діагностична робота № 11
Варіант 1
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1. На координатній площині побудувати точки Р(2;4); К(–4; 3) і М(–2; 0). Проведіть пряму МК. Через точку Р проведіть пряму, паралельну до МК, і пряму, перпендикулярну до МК.
2. У великому бідоні було в 3 рази більше молока, ніж у малому. Коли з великого бідона відлили 29 л молока, а з маленького бідона відлили 3 л, то в обох бідонах молока стало порівну. Скільки літрів молока було в кожному бідоні спочатку?
ГР-2 Виконати завдання
1. Обчисліть: - 4 – ( - 8,5 + 5,3)
2. Спростіть вираз -4х(-6у-30-12х
3. Знайдіть значення виразу 9a-5/b, якщо a=1/8 b=8 4. Знайдіть корінь рівняння 5x+0.7=4x-3.4 .
5. Знайдіть невідомий член пропорції c:7=8:9.
6. Скільки відсотків від числа 36 становить число 27?
ГР-3 Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням Упаковка містить 2/5 кг цукерок.
1) Мама на день народження Оленки купила для її друзів 15 упаковок цукерок. Скільки кілограмів цукерок купила мама?
2) Скільки знадобиться таких упаковок цукерок, щоб насипати в порожній мішечок 4 кг цукерок?
3) У ящику поміщається 10 кг цукерок. За день продали 17 упаковок. Скільки кілограмів цукерок залишилося?
одержав по 1/3 кг цукерок? (1 бал)
Підсумкова діагностична робота № 11
Варіант 2
ГР-1 Потрібно дослідити задачу і виконати її з поясненням кожної дії
1.На координатній площині побудувати точки А(2; 5); В(–1; 2) і С(3; 0). Проведіть пряму АВ. Через точку С проведіть пряму, паралельну до АВ, і пряму, перпендикулярну до АВ.
2.У першій діжці було в 4 рази більше води, ніж у другій. Коли з першої діжки відлили 27 л води, а в другу долили 15 л, то в обох діжках води стало порівну. Скільки літрів води було в кожній діжці спочатку? ГР-2 Виконати завдання
1. Обчисліть: - 5 – ( - 7,3 + 5,1)
2.Спростіть вираз -2a(-5b+4)+8a
3. Знайдіть значення виразу 7x-5:y , якщо x=1/4 y=4
4. Знайдіть корінь рівняння 7x+0.9=6x-2.7.
5. Знайдіть невідомий член пропорції a:6=3:7 .
6. Скільки відсотків від числа 25 становить число 20?
ГР-3Потрібно проаналізувати вихідні дані та певну вимогу до завдання, розв’язати одержану задачу та записати її розв’язання з поясненням чи обґрунтуванням Упаковка містить 4/25 кг льодяників.
1) Сергійко з друзями купили 10 упаковок льодяників. Скільки кілограмів льодяників купили хлопці?
2) Скільки знадобиться таких упаковок льодяників, щоб насипати в порожній мішечок 4 кг льодяників?
3) У коробці поміщається 9,6 кг льодяників. За день продали 35 упаковок. Скільки кілограмів льодяників залишилося? (
4) Скільки потрібно взяти повних упаковок льодяників, щоб кожний із чотирьох друзів Сергійка одержав по 4/5 кг цукерок?
про публікацію авторської розробки
Додати розробку