Діофантові рівняння. Розв'язування рівнянь в цілих числах.

Діофантові рівняння.

Розв’язування рівнянь в цілих числах

Зміст

Вступ………………….........................................................................................................4

Розділ 1

Загальні теоретичні відомості………………………………………………………….7

1.      Діофант і його труди ..............................................................................................7
2.      Діофантові рівняяння з одним невідомим……………………………………….9
3.      Невизначені рівняння першого порядку виду ax + by = c ...............................10

1.3.1. метод перебору……………………………………………………………12

          1.3.2. метод послідовного розподілу (спуску)....................................................13

4.      Невизначені рівняння другого порядку ……………………………………..15 

Розділ 2

Приклади розв’язування діофантових рівнянь ……………………………………18

2.1. Розв’язання лінійних діофантових рівнянь……………………………………..18

2.2. Знаходження всіх цілих розв’язків діофантових рівнянь вищих порядків…..21

Висновки…………………………………………….......................................................25

Список використаної літератури…...…….………………………………………….27

Додаток.………………………………………………………………………………….28

Вступ

„Математика не лише вчить мислити,

а й уселяє віру в безмежні сили людського розуму.

Вона виховує волю, характер”.

Василь Сухомлинський

 Навколишній світ, потреби народного господарства, а часто, і повсякденні клопоти ставлять перед людиною все нові і нові завдання, вирішення яких не завжди очевидно. Часом те чи інше питання має під собою безліч варіантів відповіді, через що відбуваються труднощі у вирішенні поставлених завдань. Як вибрати правильний і оптимальний варіант? З цим питанням прямо пов'язане рішення діофантових (невизначених) рівнянь. Діофантові рівняння цікаві і досі вивчаються математиками.

Діофантові рівняння - алгебраїчні рівняння або системи рівнянь алгебри з цілими коефіцієнтами, для яких треба знайти цілі рішення. Названі вони по імені грецького математика Діофанта, який вивчав такі рівняння. При цьому число невідомих в рівняннях повинно бути не менше двох. Діофантові рівняння мають, як правило, багато рішень, тому їх називають невизначеними рівняннями. Рівняння можуть мати невідомі не тільки в першого ступеня, а й в будь-який інший. Та й питання, які з додаткових умов, можуть виявитися найрізноманітнішими. Діофант поклав початок новому розділу математики. Він розглядав рівняння, які сьогодні ми записуємо у вигляді ах + bу = с, де а, b і з - цілі числа. Такі рівняння тепер називають «діофантових», розділ математики, що вивчає їх «Диофантова аналізом», у свою чергу Діофантом аналіз є частиною виключно цікавого розділу сучасної математики - теорії чисел.

Зазвичай, довільне рівняння (але, як правило, все-таки з цілими коефіцієнтами) отримує титул "диофантово", якщо хочуть підкреслити, що його потрібно вирішити в цілих числах, тобто знайти всі його рішення, які є цілими. Діофант цікавився вирішенням рівнянь у цілих числах ще в третьому столітті нашої ери і, треба сказати, робив це дуже успішно.

        Рішення рівнянь у цілих числах - один з найкрасивіших розділів математики. Жоден великий математик не пройшов повз теорії діофантових рівнянь. Ферма, Ейлер, Лагранж, Гаусс, Чебишев залишили незгладимий слід в цій цікавої теорії.

         Незважаючи на зусилля багатьох поколінь видатних математиків, таких як Піфагор (VI ст до н. Е.), Діофант (III ст), Ферма (XVII в), Ейлер (XVII в), в цій області відсутні загальні методи вирішення невизначених рівнянь.

У роботі розглядаються невизначені рівняння першого ступеня, тобто рівняння виду ах + bу = с, де а, b і з - цілі числа ,; з'ясовуються умови існування рішень таких рівнянь, пропонуються рішення методом перебору, методом послідовного ділення (спуску).

        У ході своїх досліджень і знайомства з теорією питання я висунула мету своєї роботи: навчитися вирішувати діофантови рівняння і задач, що зводяться до них.

Завдання моєї роботи:

- Познайомитися з теоретичним блоком, пов'язаним з особою Діофанта-вченого і його математичними дослідженнями;

- Класифікувати діофантові рівняння;

- Навчитися розв'язувати рівняння в цілих числах різних рівнів складності і класифікувати методи рішень;

- зробити висновки;

- На допомогу вчителю створити додаток, в який входитиме добірка різних завдань.

Після постановки завдань і знайомства з теорією я висунула гіпотезу моєї роботи: вміння вирішувати діофантові рівняння корисно не тільки при підготовці до математичних олімпіад, вони також можуть описувати і побутові ситуації, що зустрічаються на нашому життєвому шляху.

Об'єкт мого дослідження - діофантові рівняння.

Методи, якими я користувалася при виконанні наукової роботи: аналіз, класифікація, спостереження та узагальнення.

Новизна моєї роботи полягає в добірці завдань, здатних описати життєві ситуації для використання на уроках математики.

         Практична значимість моєї роботи полягає у використанні її на поглиблених заняттях з математики, при підготовці до математичних олімпіад.

Розділ 1. Загальні теоретичні відомості

1.           Діофант і його труди

           Діофант представляє одну з найбільш важких загадок в історії науки. Нам не відомо ні час, коли він жив, ні попередники, які працювали б в тій же області.

          Проміжок часу, коли міг жити Діофант, складають півтисячоліття! Нижня грань визначається без праці: у своїй книзі про багатокутні числа Діофант неодноразово згадує математика, який жив у середині другого в. до н.е. З іншого боку, в коментарях Теона Олександрійського до «Альмагесту» знаменитого астронома Птолемея поміщений уривок з твору Діофанта. Теона жив у середині четвертого ст.н.е. Цим визначається верхня грань цього проміжку. Отже, 500 років!

Французький історик науки Поль Таннрі, видавець найбільш повного тексту Діофанта, спробував звузити цей проміжок, він визначив, що час життя Діофанта - середина третього століття нашої ери. Зате місце проживання Діофанта добре відомо - Олександрія, центр наукової думки.

Отже, жив Діофант, мабуть, в III в. н. е., решта відомі нам факти його біографії вичерпуються таким віршем-загадкою, за переказами вигравіруваним на його надгробку:

Подорожній! Поховано тут Діофанта.

І числа розкажуть тобі,

Який дивний шлях він життєвий пройшов.

Шосту частину його становило дитинство.

Минула частина дванадцята –

І пухом покрилось його підборіддя.

Сьому – в бездітному шлюбі прожив Діофант.

Минуло п’ять літ. Ощасливлений був він

Народженням первістка – сина,

Якому судилася лише половина життя його батька.

У глибокій журбі старець закінчив шлях на землі,

 Ще проживши років чотири з часу, коли сина не стало.

Скажи, віку якого досягши славетний помер Діофант».          

        Використовуючи сучасні методи вирішення рівнянь можна порахувати, скільки років прожив Діофант.

Нехай Діофант прожив x років. Складемо і вирішимо рівняння:

.

Помножимо рівняння на 84, щоб позбутися від дробів:

Таким чином, ми дізнаємося, що Діофант одружився в 33 роки, став батьком у 38 років, втратив сина на 80-му році і помер у 84 роки.

Найбільш загадковим видається творчість Діофанта. У розвиток вчення про рівняння Діофант зробив внесок більший, ніж будь-хто інший з учених стародавньої Греції. На жаль, у нього не було послідовників, він став останнім з великих математиків давньої Греції. В кінці IV ст. н.е. Греція піддалася опустошительному навалі римських легіонерів. Велетенська Олександрійська бібліотека, один каталог якої налічував 120 томів, була знищена. Грецька наука занепала.

        З творів Діофанта до наших днів дійшло два: "Про багатокутних числах" і "Арифметика". Однак збереглися вони не повністю. «Арифметика» Діофанта - це збірник задач (всього 189), кожна з яких забезпечена рішенням і необхідними поясненнями. До нас дійшло шість з тринадцяти книг, які були об'єднані в «Арифметику», стиль і зміст цих книг різко відрізняються від класичних античних творів із теорії чисел і алгебри, зразки яких ми знаємо по «Початкам» Евкліда, його «Даним», лемам з творів Архімеда і Аполлонія. «Арифметика», безсумнівно, стала результатом численних досліджень, які залишилися зовсім невідомими. Ми можемо тільки гадати про її коренях, і дивуватися багатству і красу її методів і результатів.

         У «Арифметиці» вражає не тільки абсолютно нова мова, не тільки сміливе розширення області чисел, але і особливо ті проблеми, які ставить і вирішує Діофант. Завдання в «Арифметиці» Діофанта ретельно підібрані і служать для ілюстрації цілком певних, строго продуманих методах. Як це було прийнято в давнину, методи не формулюються в загальному вигляді, а повторюються для вирішення однотипних завдань.

2.           Діофантові рівняння із одним невідомим

, де - цілі числа.

Теорема. Якщо рівняння з цілими коефіцієнтами має цілий корінь, то цей корінь є дільником числа (вільного члена рівняння). Таким чином, при відшуканні цілих коренів рівняння з цілими коефіцієнтами досить випробувати лише дільники вільного члена.

Задача 1. Розв’язати в цілих числах рівняння

.

Розв’язання. Вільний член рівняння має наступні подільники .

Серед цих чисел і будемо шукати цілі корені даного рівняння, підстановкою

переконуємося, що коренями є числа 1 і - 3.

Відповідь: .

Задача 2. Розв’язати в цілих числах рівняння

2x⁴ + 7x³ - 12x² - 38x + 21 = 0.

Розв’язання. Вільний член рівняння має наступні дільники  .

Підстановкою у вихідне рівняння переконуємося, що з цієї безлічі тільки

число -3 є його цілим коренем.

Відповідь: х = - 3.

 Задача 3. Розв’язати в цілих числах рівняння

х⁵- 5х⁴ - 3х³ + 15х² + 2х - 10 = 0

Розв’язання. Так як число -10 має дільниками тільки числа 1, 2, 5, 10, і -1, -2, -5, -10, то ми повинні підставити всі ці дільники в рівняння замість . Неважко переконатися, що з них тільки числа 1, 5, -1 задовольняють рівнянню. Ці числа і є відповіддю до рівняння.

Відповідь: х = 1, х = 5, х = -1.

3.         Невизначені рівняння першого порядку виду ax + by = c

        Існують різні степені невизначених рівнянь, і чим вище степінь, тим більш складним є вирішення невизначеного рівняння. Довгий час сподівалися знайти загальний спосіб рішення діофантових рівнянь. Однак у 1970р. ленінградський математик Матіясевіч довів, що такого загального способу бути не може. Ми розглянемо невизначені

рівняння I-го порядку виду ax + by = с.

        Загальновідомо, що графіком лінійного рівняння з двома невідомими ах + bу = с є пряма лінія. Координати кожної точки цієї прямої - рішення даного рівняння. Таким чином, воно має нескінченну безліч рішень. Тому рівняння з кількома змінними називається невизначеним.

          Рівняння виду ax + by = c є одним з найпростіших невизначених рівнянь I-го порядку, але незважаючи на це, вирішити таке рівняння вельми не просто.

         Розглянемо два методи рішення невизначених рівнянь виду ax + by = c: метод перебору і метод «спуску».

   Неважко довести, що якщо ми знаємо одне конкретне рішення рівняння, то зможемо знайти всі рішення рівняння ax + by + c = 0. Нехай пара х₀, у₀ є рішення даного рівняння. Тобто рівність ax₀ + by₀ + c = 0 тотожне задовольняється. Віднімемо з вихідного рівняння отримане і отримаємо

a (x-x₀) + b (y-y₀) = 0. Так як a і b взаімно прості, то множник чисельника (x-x₀) повинен ділитися на b, а множник чисельника (y-y₀) повинен ділитися на a. Звідки випливає, що x = x₀ - bt, y = y₀ + at, де t - довільне ціле число.

Теорема 1. Якщо числа a і b - взаємно прості, то рівняння ax + by = 0 має нескінченно багато рішень в цілих числах, які знаходяться у взаємно однозначній відповідності з безліччю цілих чисел Z (тобто можуть бути занумеровані цілими числами) і описуються формулою    хn = bn, yn = -аn, де n Z.

Теорема 2. Якщо найбільший спільний дільник d коефіцієнтів a і b більше 1, а вільний член с не ділитися на d, то рівняння ax + by = c не має рішень в цілих числах.

Теорема 3. Будь - яке рівняння ax + by = c, де НСД (a; b) = 1. Має хоча б один розвязок в цілих числах.

Теорема 4. Якщо числа a і b - цілі, то безліч значень функції f (x; y) = ах + bу від двох цілочисельних аргументів х і у збігаються з безліччю чисел, кратних

d = НСД (a; b), тобто с множина .

Теорема 5. Якщо числа a і b - взаємно прості. То рівняння ax + by = c має нескінчену множину розвязків в цілих числах, які знаходяться у взаємному однозначній відповідності з безліччю цілих чисел Z (тобто можуть бути занумеровані цілими числами) і описуються формулою хn = х₀ + bn, yn = у₀ - an, де n Z, а х₀, у₀ - приватне рішення (яке існує в силу теореми 3)

1.   Метод перебору

Метод перебору включає в себе перебір чисел замість змінних х і у, з урахуванням, що рівняння при певному підборі чисел перетворюється у вірну рівність.

         Приклад 1. Розглянемо рівняння: 4,5х + 6у = 57.

Потрібно знайти всі натуральні значення змінних х та у.

Розв'язання: Помножимо обидві частини рівняння на 2, щоб позбутися від дробових чисел, отримаємо               9х + 12у = 114.

Виразимо  x  через  y:             

Потім використаємо метод перебору (враховуючи, що у N):

Таким чином, підставляючи замість y натуральні числа, отримали відповідні значення x (причому х і у N). Вибираємо x ∈ N. Таким чином, рівняння має три рішення: (2;8), (6;5), (10,2).

Приклад 2.   У клітці сидять кролики і фазани, всього у них 18 ніг. Дізнатися, скільки в клітці тих і інших?

Розв'язання: Складемо рівняння з двома невідомими змінними, в якому х - число кроликів. у - число фазанів:

                              4х + 2у = 18, або 2х + у = 9.

Виразимо у через х: у = 9 - 2х.

Далі скористаємося методом перебору:

Таким чином, задача має чотири розвязки: (1;7), (2;5), (3;3), (4;1).

2.                        Метод «спуску»

Перебір варіантів при вирішенні рівняння в цілих числах часто виявляється досить трудомістким. Тому розглянемо ще один старовинний прийом - метод «спуску» (або метод розсіювання). Таким методом розвязання діофантових рівнянь I-го порядку з цілими коефіцієнтами займалися ще в Стародавній Індії. Цим способом і в наш час вирішують такі рівняння.    

         Приклад. Розв’язати рівняння першого ступеня 7х - 11у = 36 в цілих числах.

Розв'язання: Виберемо невідоме, що має найменший по модулю коефіцієнт, і виразимо його через інше невідоме:

Далі, із отриманого дробу виділимо цілу частину:

                           (1)

Число х буде цілим, якщо цілим буде значення дробу.

А для цього потрібно, щоб 1 + 4у було кратне 7. Нехай   тобто 1 + 4у = 7z,   де z -  ціле число.

 Ми отримали нове рівняння з двома змінними, коефіцієнти якого по модулю менше коефіцієнтів первісного рівняння.

Вирішувати його тепер потрібно щодо змінних у і z. Діючи за цим же принципом, висловимо змінну у через z:         (2)

          Для того, щоб у виявилося цілим, необхідно щоб 3z - 1 без залишку ділилося на 4. Нехай = u,  тобто необхідно, щоб виконувалася умова 3z - 1= 4u, де u - ціле число. Звідси вже за відпрацьованою схемою з 3z – 1 = 4u     отримаємо 

            (3)

 Число z буде цілим, якщо число u + 1 буде  кратне 3. Нехай   = t. Звідси u + 1 = 3t , де t - ціле число. Виразимо змінну u через t:  u = 3t - 1     (4)

 Дробів більше нетмає. «Спуск» закінчився, будемо «підніматися вверх».

 Виразимо через змінну t спочатку z, підставивши (4) в (3):

    (5)

 Потім виразимо через t змінну у, підставивши (5) в (2):      (6) 

 І, нарешті, виразимо х через t, підставивши (4) в (3):

Таким чином, х = 11t + 2, у = 7t - 2.

 Отриманий результат можна перевірити за допомогою його підстановки у вихідне рівняння: 7(11t + 2) - 11(7t - 2) = 36 при будь - якому t.

 Надаючи змінній t цілі значення, отримаємо цілі рішення вихідного рівняння. Зрозуміло, що їх буде безліч.

Якщо ж нас зацікавлять натуральні рішення, то накладемо додаткову умову 7t – 2 > 0 і  11 t + 2 > 0.

Якщо записати розвязок у вигляді х = 2 + 11t, у = -2 + 7t і зауважити, що пара (2; -2) – розв’язок рівняння при t = 0, то можна побачити їх зв'язок з коефіцієнтами а і b. І дійсно, є теорема, яка стверджує, що якщо (x₀; y₀) - будь-який розв’язок рівняння ах + bу = с, то всі його розв’язки задаються формулами: x = x_0 + bt, y = y_0-аt (t- будь ціле число).

  Беручись за пошуки розв’язання невизначеного рівняння, ми припускали, що цілочисельне рішення у нього неодмінно є. Але чи завжди можливо вирішити рівняння виду ax + by = c в цілих числах?

        Відзначимо, що якщо коефіцієнти а, b і c невизначеного рівняння мають загальним множником деяке ціле число, відмінне від 1, то на нього можна розділити обидві частини рівняння. Тому будемо вважати що а, b і c - числа взаємно прості.

Зауважимо також, що якщо коефіцієнти при х і у мають загальний множник, якого не має вільний член с, то рівняння не може мати цілих рішень. Наприклад, рівняння 35х - 20у = 14 не має рішення в цілих числах (а тим більше в натуральних). Так як, припустити, що х і у - цілі числа, то 35х - 20у ділилося б на 5, тоді як права частина рівняння - число 14 не ділиться на 5. Іншими словами, 14 не ділиться на НСД (35; 20)

Ще одне зауваження. Рівняння краще розв’язувати щодо невідомого, коефіцієнт при якому менше по модулю. У цьому випадку буде виконано найменшу кількість проб.

         При виконанні роботи, на конкретних прикладах я переконалася в тому, що:

1. Якщо вільний член з невизначеного рівняння ax + by = c не ділиться на  

НСД (a, b), то рівняння не має цілих коренів. Так само вірно і наступне твердження: якщо число з ділиться на НСД (а; b), то рівняння ах + bу = с має цілі розв’язки.

          2) Якщо коефіцієнти a, b є взаємно простими числами, то рівняння має, принаймні, однин цілий розв’язок.

         3) Невизначене рівняння ax + by = c, в якому a, b - взаємно прості числа допускає нескінченну безліч цілих розв’язків. Всі ці розв’язки задаються формулами: x = α + bt, y = β - at, де (α, β) - деякі рішення рівняння, a t належить безлічі цілих чисел.

1.4. Невизначені рівняння другого порядку  x² + y² = z²

вузли.

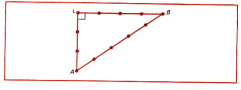
У точці С де треба було побудувати прямий кут, вбивали кілочок, мотузку натягували в напрямку, потрібному будівельникам, забивали кілочок в точці В (СВ = 4) і натягували мотузку так, щоб АС = 3 і АВ = 5. Трикутник з такими довжинами сторін називають єгипетським. Ми, звичайно, розуміємо, що безпомилковість такої побудови випливає з теореми, зворотної теоремі Піфагора. Дійсно, 3² + 4² = 5². Говорячи інакше, числа 3, 4, 5 - корені рівняння .

Відразу ж виникає питання: чи немає у цього рівняння інших цілочисельних рішень?  Один із шляхів вирішення рівняння в цілих числах виявився досить простим. Запишемо підряд квадрати натуральних чисел, відокремивши їх один від одного комою. Під кожною комою запишемо різницю між послідовними квадратами:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196 … .

   3,  5,  7,  9,  11,  13,  15,  17,  19,  21,  23,  25,  27 … .

А тепер увага! Чи немає в нижньому рядку квадратних чисел? Є! Перше з них 9 = 3², над ним 16 = 4² і 25 = 5², відома нам трійка 3, 4, 5.

Наступне квадратне число в нижньому рядку 25, йому відповідає 144 і 169, звідси знаходимо другу відому нам трійку 5, 12, 13 і т. д. Звідси ми маємо право сформулювати таку теорему: Кожне непарне число є різниця двох послідовних квадратів. Складати такі рядки - досить нудне і трудомістке заняття. За формулами знаходити такі трійки чисел і простіше і швидше. Перевіримо що якщо - непарне число, тоді і .  Перевіримо також, що в цьому випадку рівність виконується, тобто числа, знайдені за таким правилом, завжди будуть складати розвязок даного нам невизначеного рівняння. Це рівняння будемо називати «рівнянням Піфагора», а його розвязок - «піфагоровими трійками». За цим правилом можна отримати вже відомі нам трійки: якщо то отримали першу піфагорову трійку;

якщо тоді і  - друга трійка і т.д.

Приклад 1. Знайти всі пари натуральних чисел, що задовольняють рівнянню

.

Розв’язання. Розклавши ліву частину рівняння на множники і запишемо рівняння виду (х - у)(х + у) = 69. Так як дільниками числа 69 є числа 1, 3, 23 і 69, то 69 можна отримати двома способами: 69 = 1 · 69 і 69 = 3 · 23. Враховуючи, що, х - у > 0, отримаємо дві системи рівнянь, розв’язавши які ми зможемо знайти шукані числа:

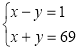   або   .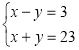

Перша система має розв’язок , а друга система має розвязок .

Відповідь .

Приклад 2. Доведіть, що рівняння не має цілих розв’язків.

Розв’язання. Розкладемо ліву частину рівняння на множники і запишемо дане рівняння у вигляді . 1 випадок. Нехай у = 0, тоді початкове рівняння має вигляд . Отже , але це число не ціле. Тоді, якщо у = 0 дане рівняння не має цілих розвязків. 2 випадок. Нехай , тоді всі пять множників в лівій частині рівняння різні. З іншого боку число 33 можна представити у вигляді добутку максимум чотирьох різних множників (33 = 1 · 3 · 11 або 33 = -1 · 3 · (-11) · 1 і т.д.). Отже, при   дане рівняння також не має цілих розв’язків. Слід зробити висновок про те, що розв’язання рівнянь зводяться до знаходження натуральних чисел; за допомогою «Піфагорової трійки».

Розділ 2. Приклади розв’язування діофантових рівнянь

2.1. Розв’язання лінійних діофантових рівнянь

Приклад 1.

Вміння розв’язувати діофантові рівняння дає можливість виконати наступний математичний фокус.

Якщо помножити дату свого дня народження на 12, а номер місяця на 31 і знайти суму, то за такою сумою можна визначити дату народження.

Якщо, наприклад, задумана дата – 9 лютого, то наступні дії будуть такими:

За останнім числом 170 потрібно визначити задуману дату.

Задача зводиться до розв'язку рівняння з двома невідомими

у цілих, додатних числах, причому число місяця