Добірка вправ з теми" Застосування методу інтервалів та систем рівнянь другого степеня для розв’язування прикладних задач. 1. Підприємницька компетентність.

Застосування   методу інтервалів та систем рівнянь другого степеня для розв’язування  прикладних задач.

 1. Підприємницька компетентність.

 

А)Функція сукупних витрат фірми РС= Q² + 4Q + 7,   Q – кількість продукції. Ціна одиниці продукції р=12. При яких обсягах виробництва фірма матиме економічний прибуток ЕР ?

 

Оскільки  ЕР = ТR – РС, , де  виторг ТR = р Q = 12 Q . Тоді ЕР = 12 Q – Q² - 4 Q – 7. Фірма матиме прибуток, якщо ЕР0. Тобто:  - Q² +8 Q - 70  або    Q² - 8 Q – 7 0 .

За теоремою Вієта знайдемо значення  Q:  1 і 7 і, скориставшись методом інтервалів для розв’язування нерівностей, маємо:

                           1 Q  7.

 

             1                           7

Висновок. Якщо обсяг  виробництва буде в межах від 1 до 7, то  фірма матиме економічний прибуток.

 

 Б). Нехай у короткостроковому періоді виробнича функція залежить тільки від чисельності персоналу, похідна якої має вигляд:  = 12 Р – 0,6Р², де С – похідна функції випуску продукції , Р – кількість працюючих. Якою має бути чисельність персоналу, щоб випуск продукції досягав максимального значення?

 

       Щоб випуск продукції досягав максимального значення , то необхідно, щоб С 0 , тобто

                                                                                                        12Р – 0,6Р² 0

                                                                                                        0,6Р ( 20 – Р) 0

 

          Застосувавши метод розв’язання нерівності, маємо значення Р =0,  Р =20.                                                                                  . Звідки     Р ( 0; 20)

                       0                20

Висновок. Випуск продукції буде максимальним при кількості працюючих 19 - 20 чоловік.

 

В) Автослюсар отримав завдання на виготовлення кількох комплектів деталей для восьмициіндрованих автомобільних двигунів. Слюсар підрахував, що коли йому вдасться підвищити продуктивність праці на 0,1 дет/год, то він зможе виконати завдання на 12 год раніше строку. А якщо ще на 0,5 дет/год, то виконає завдання на 36 год раніше строку. Скільки  деталей потрібно виготовити слюсарю? Яка кількість деталей на кожний двигун?

 

Якщо позначити через х год – нормативний час виконання завдання, а через у дет.- нормативну кількість деталей, що виготовляються за цей час, тоді можна записати умову задачі так:

; ; Від першого рівняння, помноженого на  число 3, віднімемо друге і отримаємо:    -0,3х+18=0;   х=60 год.  Тоді у = 0,4 дет/год.

60*0,4 =24 деталі;    24 : 8 = 3 деталі.

Висновок. Автослюсар отримав завдання виготовити 24 деталі, по 3 деталі на кожний двигун.

 

Г) На конвеєрних лініях молочного заводу виготовляють два сорти морозива: шоколадне і полуничне. За 8 год роботи з кожної лінії сходить однакова кількість порцій морозива. В однин із днів на шоколадній лінії трапилася поломка, внаслідок якої денний випуск шоколадного морозива скоротився на 2 тис порцій. При  цьому виявилося, що на випуск однієї порції шоколадного морозива фактично витрачалося на 1,2 с більше, ніж на випуск однієї порції полуничного. Скільки порцій шоколадного і полуничного морозива було випущено в цей день?

Позначимо через х кількість порцій полуничного морозива, що випускається за 8 год=480 хв, а за у – кількість порцій шоколадного, що випускався в день поломки лінії. 1,2 с = 0,02 хв.

Тоді 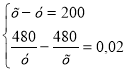; 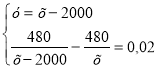.  Звівши до спільного знаменника, маємо      

                                    рівняння:     480х-480(х-2000)=0,02х (х-2000).

Спростивши рівняння, одержимо х² – 2000х – 480000 =0,

                                                          х = 80000, х = - 60000. Умову задачі задовольняє число  8000 .

Висновок. В цей  день було випущено 8000 порцій полуничного і 6000 порцій шоколадного морозива.  

 

2.Дослідницька компетентність.

 

А)  Бурдж Халіфа – найвища споруда в світі, що розташована в місті Дубай, Об’єднані Арабські Емірати. Вона сягає  828  метрів і складається зі 162 поверхів. Вежу можна побачити з відстані 90 км!  Бейс-джампінг – екстремальний вид спорту. B.A.S.E. – скорочення слів Building, Antenna, Span, Earth – об’єктів, з яких стрибають бейс-джампери.

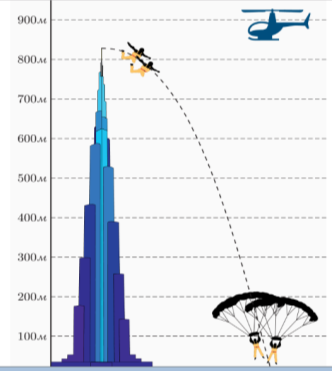В 2014 році двоє французьких джамперів Фред Ф’юген та Вінс Реффет встановили новий рекорд Гіннеса - найвищий бейс-стрибок з будівлі –828 метрів. Вони стрибнули з самісінької кінцівки шпиля Бурдж-Халіфи.

А тепер спробуємо описати цей стрибок математично і знайти скільки часу було у джамерів, щоб розкрити парашут для безпечного для життя стрибка.

На примітивному рівні, звичайно.

Висота Бурдж Халіфи – 828метрів. Залежність висоти від часу при вільному падінні описується квадратичною функцією:    h(t) = h0+v0t−

g ≈ 9.8м/c²– прискорення вільного падіння,

h0– початкова висота, v0– початкова швидкість.

У випадку наших джамперів: h=828м, v=0м/c

Математичною моделлю задачі є рівняння:

h(t) = 828−4,9t²

 Xлопці розкривають парашути на висоті близько 100 метрів. За інформацією з інтернет-форумів для джамперів, стало зрозуміло, що ця висота є критичною: якщо розкрити парашут нижче, такий стрибок може стати фатальним.

Час, який є у джамперів для того, щоб розкрити парашут безпечно для життя, можна визначити з нерівності:    828−4,9t²  >100;       828−4,9t²  −100 > 0;     728−4,9t²  > 0;   

 t²  −148,57 < 0;        (t−12,19)(t+12,19) <0.

Значення t = ± 12,19 перетворюють функцію в лівій частині нерівності на нуль і розбивають числову вісь на три проміжки:

Використаємо той інтервал, де функція є від’ємною – тобто 

   t  (−12,19;12,19).

Оскільки  час – величина невід’ємна , тому треба накласти  

    -12,19                 12,19               додаткову умову: t ≥ 0.    В результаті маємо  t  (0;12,19).

 

Висновок.  Ці  бентежні хлопці мали трохи більше, ніж 12,2 секунд для того, щоб насолодитися вільним падінням безпечно для життя.

3.Екологічна компетентність.

 

А) Є 6 г радіоактивної речовини  з періодом піврозпаду 6 років і 24 г радіоактивної речовини з періодом піврозпаду 3 роки. Через скільки років маса першої речовини буде рівна або більша маси другої речовини?

 

Рівняння радіоактивного розпаду речовини має вигляд  m = m 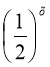, де m -початкова маса радіоактивної речовини, m – маса речовини, що лишилась внаслідок розпаду після х періодів піврозпаду.  х = - відношення часу протікання реакції до періоду піврозпаду даної речовини. За даними задачі через  t років маса першої речовини становить

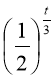 6г,  а другої  -  24г. 

Математичною моделлю задачі буде нерівність :     6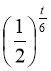 24.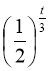 

З умови зрозуміло, що період піврозпаду першої речовини вдвічі більший від періоду піврозпаду другої речовини.

Отже,    і, зробивши заміну у нерівності 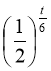 = у,

          маємо нову нерівність:   6у -24у² 0.

Застосуємо метод інтервалів:  6у( 4у -1) 0      

 

                                                                                                     0                            

у  . Повернемось до заміни:      0 .

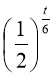
Зрозуміло , що  2,  тобто t 12.

 

Висновок. Через 12 років маси речовин будуть рівними, а більше, ніж через  12  років  маса першої речовини буде більшою за масу другої речовини.