Зошит контролю знань "Геометрія, 9 кл"
Зошит містить контрольні роботи з геометрії по темах для учнів початкового та середнього рівнів навченості у 9 класі. кожна контрольна робота містить теоретичний матеріал у малюнках, зразки розв"язаних задач і аналогічні контрольні завдання для оцінювання.
9кл Тема 1. Синус, косинус і тангенс кутів від 00 до 1800.
Залікові запитання І –ІІ рівня.
 Запам’ятай !
Запам’ятай !
![]()

![]()

![]()


 Sin
Sin ![]() =
= ![]() cos
cos ![]() =
=![]() tg
tg![]() =
=![]()
a c c a
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() в в
в в
![]()

Продовж запис. n

![]()
 a) sin
a) sin ![]() =…… c) sin
=…… c) sin ![]() =…
=…
р к cos ![]() =… m c cos
=… m c cos ![]() =…
=…
tg ![]() =… y
=… y
![]()
с b) sin ![]() =…
=…
tg ![]() =… z
=… z
Знайди правильну відповідь.
-
 Відомо, що у трикутнику АВС кут С =900, АВ = 5см, АС = 3см, ВС = 4см Тоді sin
Відомо, що у трикутнику АВС кут С =900, АВ = 5см, АС = 3см, ВС = 4см Тоді sin  В дорівнює: А
В дорівнює: А 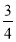 ; Б
; Б 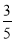 ; В
; В 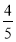 ; Г
; Г 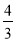
С В
 N
N
-
У
 МNК:
МNК:  К=900, NK=6см, MK=18см,
К=900, NK=6см, MK=18см,
MN=6![]() см . Тоді правильно, що:
см . Тоді правильно, що:
М К А sin N=![]() ; Б tg M=
; Б tg M=![]() ; B cos N=
; B cos N=![]() ;
;
 Г tg N=
Г tg N=![]() .
.
Запам’ятай !
а)Якщо 00![]() 900, то sin
900, то sin ![]() = «+», cos
= «+», cos ![]() = «+»,tg
= «+»,tg ![]() = «+».
= «+».
Якщо 900![]() 1800, то sin
1800, то sin ![]() = «+», cos
= «+», cos ![]() = «-»,tg
= «-»,tg ![]() = «- ».
= «- ».
б) sin ![]()
![]() 1, cos
1, cos ![]()
![]() 1.
1.
- Розстав правильно знаки: sin 480= «…», sin 1080= «…», sin 1480= «…»,
cos 1060= «…», cos 760= «…», cos 1760= «…»,
tg 230 = «…», tg 1230 = «…», tg 30 = «…».
4.Знайди можливу НЕ правильну відповідь :А. sin N=0,78; Б. tg M=0,04; B. cos N=5; Г. tg N=1,5.
9 кл. Тема 1. Теорема косинусів і синусів.
Залікові запитання І-ІІ рівня.
- Скористайтесь таблицею значень тригонометричних функцій та вкажіть правильну відповідь:
|
А |
Б |
В |
Г |
|
sin 300=0,5 |
sin 900=0 |
sin 1500= -0,2 |
sin 1200= -1 |
2.У трикутнику АВС АВ = 8см, АС = 6см, ВС = 4см. Вкажіть найбільший кут.

 Запам’ятай !
Запам’ятай !
![]()
![]()
 Теорема косинусів: Теорема синусів:
Теорема косинусів: Теорема синусів:
с2 = а2 + в2 – 2ав cos ![]()
![]()
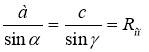
а в
![]()
![]()
![]()
с
3. За даними , вказаними на малюнку, знайди вірний запис теореми косинусів.
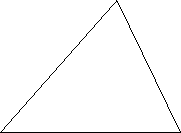
![]()
![]()
![]()
![]()
A Б
a c a2 =b + c – 2bc cos ![]() c2 = a2 +b2 - ab cos
c2 = a2 +b2 - ab cos![]()
![]()
B Г
![]()

![]()
![]() a2 = b2+c2 – 2bc cos
a2 = b2+c2 – 2bc cos![]() c2= a2 +b2 – 2bc cos
c2= a2 +b2 – 2bc cos![]()
![]() b
b
4.В теоремі синусів кожне з відношень ![]() ;
; ![]() ;
; ![]() дорівнює:
дорівнює:
А. діаметру кола, вписаного в трикутник Б. діаметру кола, описаного навколо трикутника
В. довжині кола, описаного навколо трикутника Г. радіусу кола, описаного навколо трикутника.
- Довжина сторони трикутника 10 см, а синус кута, що лежить навпроти цієї сторони дорівнює 0,2. Чому дорівнює радіус описаного навколо цього трикутника кола?
|
А |
Б |
В |
Г |
|
0,5 |
0,2 |
50 |
20 |
-
Якщо у трикутнику є тупий кут і позначений він
 , тоді знайди правильний запис теореми косинусів для цього трикутника
, тоді знайди правильний запис теореми косинусів для цього трикутника
|
А |
Б |
|
a2 =b + c – 2bc cos |
c2 = a2 +b2 - ab cos |
|
В |
Г |
|
a2 = b2+c2 + 2bc |
c2= a2 +b2 – 2ав cos |
9 кл. Тема 1. Площі трикутника .
Залікові запитання І – ІІ рівня.
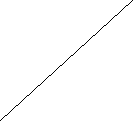
Запам’ятай ! a
![]()
![]()

![]()
![]()

![]()
![]()
![]()
![]()
S = ![]() h h h
h h h
![]()
![]()
![]()
a a
Застосуй дану формулу до розв’язування задач.
- Обчислити площу трикутника, у якого а = 12см, h = 6см.
-
 Обчислити площу трикутника, у якого висота дорівнює 4см, а сторона, до якої та висота проведена рівна 14см.
Обчислити площу трикутника, у якого висота дорівнює 4см, а сторона, до якої та висота проведена рівна 14см.

![]()

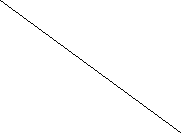
 Запам’ятай ! а
Запам’ятай ! а
 а
а ![]()
![]()
![]() S =
S =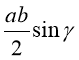
![]() в
в
в
Застосуй дану формулу до розв’язування задач.
-
Обчислити площу трикутника, у якого а = 12см, в = 6см, а sin
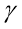 дорівнює 0,2.
дорівнює 0,2.
- Обчислити площу трикутника, довжини сторін якого 6см та 18см, а кут між ними 300.
Запам’ятай формулу Герона!

S=![]() , де а, в, с – довжини сторін трикутника
, де а, в, с – довжини сторін трикутника
р – півпериметр трикутника.
Зразок розв’язку задач.
У трикутнику довжини його сторін дорівнюють 10см, 8см та 12см. Знайти площу трикутника.
Розв’язок.
р =![]() =
= ![]() . S =
. S =![]() =
= ![]() . Відповідь.15
. Відповідь.15![]() см2.
см2.
Розв’яжи задачі за зразком.
- Довжини сторін трикутника дорівнюють 13, 14 і 15 см. . Знайдіть площу трикутника.
- Сторони паралелограма дорівнюють 25см і 29см, а одна із діагоналей – 36см. Знайдіть площу паралелограма. (Підказка! Площа паралелограма дорівнює площі трикутника,
помноженій на 2 : S![]() = 2* S
= 2* S![]() ).
).
9кл Тема 2. Метод координат на площині.
Залікові запитання І –ІІ рівня.
Зразок розв’язування задачі №1.
Знайти середину відрізків АВ і СК, якщо А (3;5) і В (7;9), а С (-4;8) і К (6; -16)
Розв’язок. А В
![]()
![]()
![]()
![]()
![]()
![]() Відповідь. (5;7) – середина відрізка АВ.
Відповідь. (5;7) – середина відрізка АВ.
![]()
![]() Відповідь. (1; -4) – середина відрізка СК
Відповідь. (1; -4) – середина відрізка СК
Розв’яжи задачу за зразком.
1. Знайти середину відрізків АВ і СК, якщо А (5;3), В (8;14), С (-6; -8) і К (14;-4).
Зразок розв’язування задачі №2.
Середина відрізка МР – точка О (-4; 12), М (8;11). Знайти координати точки Р.
Розв’язок. М О Р
![]()
![]()
![]()
![]()
Позначимо координати точки Р (х![]() ; у
; у![]() ), тоді:
), тоді: ![]()
![]()
8 + х![]() = -4* 2; 11+ у
= -4* 2; 11+ у![]() =12 * 2
=12 * 2
х![]() =-8 – 8 у
=-8 – 8 у![]() =24 -11
=24 -11
х![]() = -16 у
= -16 у![]() =13. Відповідь. Координати точки Р (-16; 13)
=13. Відповідь. Координати точки Р (-16; 13)
Розв’яжи задачу за зразком
2. .Середина відрізка МР – точка О (-8; 5), М (-3; 9). Знайти координати точки Р.
Зразок розв’язування задачі №3.
Знайти відстань між точками М та В, якщо М( 6; 8) і В ( -4; 3).
Розв’язок.
Знайдемо координати відрізка МВ: (-4 - 6; 3 - 8)=(-10; -5)
МВ = ![]() . Відповідь. Довжина МВ =
. Відповідь. Довжина МВ =![]() .
.
Розв’яжи задачу за зразком
3.Знайти відстань між точками М та В, якщо М( 7; 8) і В ( 9; -3).
![]()
Запам’ятай ! Рівняння кола : (х – а)2 +(у – в)2 = R2 ,
де (а;в) – координати центру кола, а R – довжина радіуса кола.
Зразок розв’язування задачі №4.
Записати рівняння кола з центром в точці А(-4;6) та діаметром D = 6см.
Розв’язок.
Знайдемо радіус кола: R = D:2 = 6 : 2 = 3см. Тоді рівняння кола має вигляд
(х-(-4))2 + (у-6)2 = 32; (х + 4)2 + (у – 6)2 = 9.
Розв’яжи задачу за зразком
![]() 4.Записати рівняння кола з центром в точці О(9; -5) та радіусом R = 7см.
4.Записати рівняння кола з центром в точці О(9; -5) та радіусом R = 7см.
Запам’ятай ! Рівняння прямої : у = кх + в ,
к –кутовий коефіцієнт, (х;у) – координати точки, через яку пряма проходить.
Зразок розв’язування задачі №5.
Чи проходить пряма у =5х + 6 через точку О(-4; 2)?
Розв’язок.
к = 5; у =2; х = -4. отже, 2 =5*(-4) + 6. Перевіримо рівність. 2 = -20 +6; 2 ![]() -14. Отже, пряма
-14. Отже, пряма
НЕ проходить через точку О.
Розв’яжи задачу за зразком
5. Через яку точку А(6;-1) чи В(8; 0) проходить пряма у =-3х +17? Назвати коефіцієнт цієї прямої.
9кл Тема 3. Геометричні перетворення.
Залікові запитання І –ІІ рівня.
- Рухом НЕ вважають: І. симетрію відносно точки і прямої; ІІ. поворот
ІІІ. гомотетію; IV. паралельне перенесення і поворот
|
А |
Б |
В |
Г |
|
І і IV |
лише ІІІ |
лише ІІ |
ІІ і ІІІ |
- Відносно прямої п симетричними є точки (див.малюнок):

![]()
![]()
![]() n K P C
n K P C
|
А |
Б |
В |
|
|
D I M |
P I S |
Ki T |
|
![]() D
D
![]()
![]()
![]() Т
Т
![]()
![]()

![]() Запам’ятай ! В координатах точки
Запам’ятай ! В координатах точки
![]() при симетрії відносно осі ОУ змінюємо знак Х і навпаки! F S
при симетрії відносно осі ОУ змінюємо знак Х і навпаки! F S
![]() При симетрії відносно початку координат змінюють знак і х і у М
При симетрії відносно початку координат змінюють знак і х і у М
Зразок розв’язування задачі .
Які координати точки М, якщо вона симетрична точці А(-4;7) відносно осі ОУ?
Розв’язок.
Якщо М симетрична відносно осі ОУ, то змінюємо знак біля -4. Отже М (4;7)
Розв’яжи задачу за зразком.
3.Дано точку А ( -8; -4). Які координати точки В, якщо вона симетрична А відносно початку відліку
|
А |
Б |
В |
Г |
|
(-8; -4) |
(8; -4) |
(-8;4) |
(8;4) |
4.Дано квадрат АВСК. При повороті цього квадрата на 1800 за годинниковою стрілкою навколо
точки А куди перейде вершина С ?
 А В
А В

![]() А. у точку К
А. у точку К
Б. у точку А
В. у точку В
Г. не змінить свого положення
К С
5. Точка М ( -5; 1) при паралельному перенесенні на 1 одиницю у додатному напрямі осі ОХ переходить у точку К з координатами А. ( -6; 0); Б. ( -4; 1)
В. ( -4; 2); Г. ( -5; 2).
Зразок розв’язування задачі.
Паралельне перенесення задано формулами ![]()
В яку точку при цьому паралельному перенесенні перейде точка ( -5;3).
Розв’язок.
Координати ( -5; 3) підставляємо у формули замість х та у. ![]() ;
; ![]() .
.
Відповідь. Точка ( -5;3) перейде у точку ( -8; 5).
Розв’яжи задачу за зразком.
6. В яку точку при паралельному перенесенні ![]() перейде точка ( 6; -2)?
перейде точка ( 6; -2)?
9кл Тема 4. Вектори на площині..
Залікові запитання І –ІІ рівня.
Зразок розв’язування задачі №1.
.Дано координати кінців вектора: А( 6;2) і В(8;4). Знайти координати вектора ![]() .
.
Розв’язок.
Точка А – початок вектора, точка В – його кінець. Отже, від координат кінця віднімаємо коорди-
нати початку: ( 8 -6; 4 -2) = (2;2) – координати вектора ![]() .
.
Розв’яжи задачу за зразком.
1.С (7; 5), М (6; -6); К ( -2; 8). Знайдіть координати векторів ![]() та
та ![]()
Зразок розв’язування задачі №2.
Знайдіть довжину вектора ![]() ( -4; 6).
( -4; 6).
Розв’язок. Скористаємось формулою ![]() =
= ![]() , де в
, де в![]() = -4, а в
= -4, а в![]() =6. Отже,
=6. Отже, ![]() =
=![]() =
= ![]() =
=![]() . Відповідь. Довжина вектора в =
. Відповідь. Довжина вектора в =![]() .
.
Розв’яжи задачу за зразком.
2.Знайдіть довжину вектора ![]() (11; -9).
(11; -9).
Зразок розв’язування задачі №3.
Знайдіть координати вектора ![]() , якщо к = -4,
, якщо к = -4, ![]() ( 4;-3).
( 4;-3).
Розв’язок . ![]() ( -4*4; -4*(-3)) = (-16; 12) – координати вектора.
( -4*4; -4*(-3)) = (-16; 12) – координати вектора.
Розв’яжи задачу за зразком.
3а. Знайдіть координати вектора ![]() , якщо к = 0,5,
, якщо к = 0,5, ![]() ( -94; 18).
( -94; 18).
3б. Знайдіть координати вектора ![]() , якщо м =
, якщо м = ![]() ,
, ![]() ( 15; -10).
( 15; -10).
Зразок розв’язування задачі №4.
Знайдіть скалярний добуток векторів ![]() ( -5; 23) і
( -5; 23) і ![]() (14; 2)
(14; 2)
Розв’язок . ![]() *
*![]() = -5*14+23*2 = -70 + 46 = -24.
= -5*14+23*2 = -70 + 46 = -24.
Відповідь. Скалярний добуток векторів а і в дорівнює -24.
Розв’яжи задачу за зразком.
4. Знайдіть скалярний добуток векторів ![]() ( 18; 3) і (14; -12).
( 18; 3) і (14; -12).
Зразок розв’язування задачі №5.
Знайдіть косинус кута між векторами ![]() і
і ![]() , якщо
, якщо ![]() =24 ;
=24 ; ![]() = 10, а їх скалярний добуток дорівнює 32.
= 10, а їх скалярний добуток дорівнює 32.
Розв’язок . Скористаємось формулою cos![]() =
= 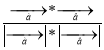 . Отже, cos
. Отже, cos![]() =
=![]() - відповідь.
- відповідь.
5. Знайдіть косинус кута між векторами ![]() і
і ![]() , якщо
, якщо ![]() =4 ;
=4 ; ![]() = 22, а їх скалярний добуток дорівнює 11.
= 22, а їх скалярний добуток дорівнює 11.


про публікацію авторської розробки
Додати розробку