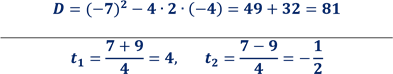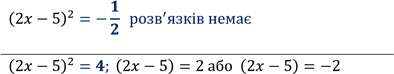Додаток. Покрокове розв'язування рівнянь, що зводяться до квадратних

Про матеріал

Покрокове розв'язування рівнянь, що зводяться до квадратних. Матеріал розрахований для учнів

Перегляд файлу

Розв’яжіть рівняння:

Розв’язання

Використаємо метод заміни змінної

Крок	Зміст дії	Результат дії
Крок 1	Замінимо змінну х² змінною t, щоб понизити степінь рівняння
Крок 2	Запишемо задане рівняння з використанням змінної t
Крок 3	Розв’яжемо квадратне рівняння . Визначимо його коефіцієнти й знайдемо дискримінант
Крок 4	Обчислимо корені рівняння t₁ та t₂
Крок 5	Повернемося до початкової заміни
Крок 6	Розв’яжемо отримані неповні квадратні рівняння	;

Відповідь:

Розв’яжіть рівняння:

Розв’язання

Крок	Зміст дії	Результат дії
Крок 1	Замінимо вираз змінною t, щоб понизити степінь рівняння
Крок 2	Запишемо задане рівняння з використанням змінної t
Крок 3	Розв’яжемо квадратне рівняння . Визначимо його коефіцієнти й знайдемо дискримінант
Крок 4	Обчислимо корені рівняння t₁ та t₂
Крок 5	Повернемося до початкової заміни

Крок 6	Розв’яжемо отримані лінійні рівняння

Відповідь:

Розв’яжіть рівняння:

Крок	Зміст дії			Результат дії
Крок 1	Замінимо вираз змінною t, щоб пони рівняння		епінь	тоді отримали	;
		зити ст
Крок 2	Запишемо задане рівнянн використанням змінної t		я з
Крок 3	Розв’яжемо квадратне рівн . Визначи його коефіцієнти й знайде		яння мо мо

Крок	Зміст дії		Результат дії
Крок 1	Замінимо вираз змінною t, степінь рівняння
		щоб понизити
Крок 2	Запишемо задане рівняння з використанням змінної t
Крок 3	Розв’яжемо квадратне рівняння . Визначимо його коефіцієнти й знайдемо дискримінант
Крок 4	Обчислимо корені рівняння t₁ та t₂
Крок 5	Повернемося до початкової заміни
Крок 6	Розв’яжемо отримані квадратні рівняння

Відповідь:

Розв’яжіть рівняння:

;

	дискримінант
Крок 4	Обчислимо корені рівняння t₁ та t2
Крок 5	Повернемося до початкової заміни
Крок 6	Розв’яжемо отримані квадратні рівняння	За теоремою Вієта: коренів немає, отже розв’язку немає	—