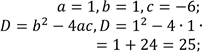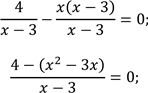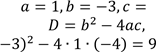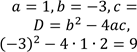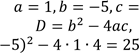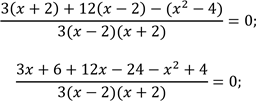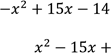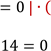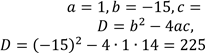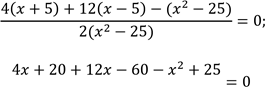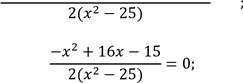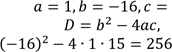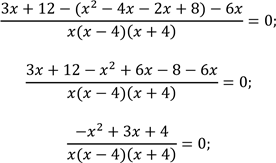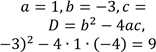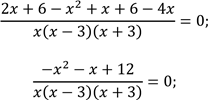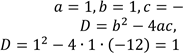Додаток. Покрокове розв'язування рівнянь, що зводяться до квадратних

Кр

ок

Зміст дії

Результат дії

Крок 1

Знайдемо область допустимих значень рівняння 

Крок 2

Перенесемо змінну х в ліву частину рівняння з протилежним знаком. Зведемо до спільного знаменника дроби в лівій частині та виконаємо дію віднімання раціональних дробів з однаковими знаменниками

Крок 3

Скористаємося правилом рівності дробу нулю:

. З урахуванням ОДЗ

розглянемо рівність чисельника нулю.  Помножимо обидві частини рівняння на (-1)

Крок 4

Визначимо коефіцієнти отриманого квадратного рівняння. 

Це зведене квадратне рівняння, яке має «зручні» коефіцієнти, тому розв’яжемо його за теоремою Вієта.

Крок 5

Перевіримо, чи задовольняють отримані корені ОДЗ рівняння.

 задовольняє ОДЗ задовольняє ОДЗ

Кр

ок

Зміст дії

Результат дії

Крок 1

Знайдемо область допустимих значень рівняння 

Крок 2

Перенесемо змінну х у праву частину рівняння з протилежним знаком. Зведемо до спільного знаменника дроби та

виконаємо дію віднімання раціональних дробів з однаковими знаменниками

Крок 3

Скористаємося правилом рівності дробу нулю:

. З урахуванням

ОДЗ розглянемо рівність чисельника нулю.  Помножимо обидві частини рівняння  на (-1)

Крок 4

Визначимо коефіцієнти отриманого квадратного рівняння. 

Це зведене квадратне рівняння, яке має «зручні» коефіцієнти, тому розв’яжемо його за теоремою Вієта.

Крок 5

Перевіримо, чи задовольняють отримані корені ОДЗ рівняння.

 задовольняє ОДЗ задовольняє ОДЗ

Кр

ок

Зміст дії

Результат дії

Крок 1

Знайдемо область допустимих значень рівняння 

Крок 2

Перенесемо доданок 4  в ліву частину рівняння з протилежним знаком. Зведемо до спільного знаменника дроби в лівій частині та виконаємо дії додавання і віднімання раціональних дробів з однаковими знаменниками

Крок 3

Скористаємося правилом рівності дробу нулю:

. З урахуванням ОДЗ

розглянемо рівність чисельника нулю. 

Крок 4

Визначимо коефіцієнти отриманого квадратного рівняння. 

Це зведене квадратне рівняння, яке має «зручні» коефіцієнти, тому розв’яжемо його за теоремою Вієта.

Крок 5

Перевіримо, чи задовольняють отримані корені ОДЗ рівняння.

 задовольняє ОДЗ  задовольняє ОДЗ

Кр

ок

Зміст дії

Результат дії

Крок 1

Знайдемо область допустимих значень рівняння 

Крок 2

Перенесемо доданок 3  в ліву частину рівняння з протилежним знаком. Зведемо до спільного знаменника дроби в лівій частині та виконаємо дію  віднімання раціональних дробів з однаковими знаменниками

Крок 3

Скористаємося правилом рівності дробу нулю:

. З урахуванням ОДЗ

розглянемо рівність чисельника нулю. 

Крок 4

Визначимо коефіцієнти отриманого квадратного рівняння. 

Це зведене квадратне рівняння, яке має «зручні» коефіцієнти, тому розв’яжемо його за теоремою Вієта.

Крок 5

Перевіримо, чи задовольняють отримані

 задовольняє ОДЗ

корені ОДЗ рівняння.

 задовольняє ОДЗ

Кр

ок

Зміст дії

Результат дії

Крок 1

Знайдемо область допустимих значень рівняння 

Крок 2

Перенесемо доданок   в ліву частину рівняння з протилежним знаком. Зведемо до спільного знаменника дроби в лівій частині та виконаємо дії додавання і віднімання раціональних дробів з однаковими знаменниками

Крок 3

Скористаємося правилом рівності дробу нулю:

. З урахуванням

ОДЗ розглянемо рівність чисельника нулю. 

Помножимо обидві частини рівняння  на (-1)

Крок 4

Визначимо коефіцієнти отриманого квадратного рівняння. 

Це зведене квадратне рівняння, яке має «зручні» коефіцієнти, тому розв’яжемо його за теоремою Вієта.

Крок 5

Перевіримо, чи задовольняють отримані корені ОДЗ рівняння.

 задовольняє ОДЗ

 задовольняє ОДЗ

Кр

ок

Зміст дії

Результат дії

Крок 1

Знайдемо область допустимих значень рівняння 

Крок 2

Перенесемо доданок   в ліву частину рівняння з протилежним знаком. Зведемо до спільного знаменника дроби в лівій частині та виконаємо дії додавання і віднімання раціональних дробів з однаковими знаменниками

Крок 3

Скористаємося правилом рівності дробу нулю:

. З

урахуванням ОДЗ розглянемо рівність чисельника нулю.  Помножимо обидві частини

рівняння  на (-1)

Крок 4

Визначимо коефіцієнти отриманого квадратного рівняння. 

Це зведене квадратне рівняння, яке має «зручні» коефіцієнти, тому розв’яжемо його за теоремою Вієта.

Крок 5

Перевіримо, чи задовольняють отримані корені ОДЗ рівняння.

 задовольняє ОДЗ

 задовольняє ОДЗ

Кр

ок

Зміст дії

Результат дії

Розкладемо знаменники дробовораціональних виразів на множники

Крок 1

Знайдемо область допустимих значень рівняння 

Крок 2

Перенесемо дробово-раціональний вираз 

   у праву частину рівняння з

протилежним знаком. Зведемо до спільного знаменника дроби та виконаємо дію віднімання раціональних дробів з однаковими знаменниками

Крок 3

Скористаємося правилом рівності дробу нулю:

. З урахуванням

ОДЗ розглянемо рівність чисельника нулю. 

Помножимо обидві частини рівняння  на (-1)

Крок 4

Визначимо коефіцієнти отриманого квадратного рівняння. 

Це зведене квадратне рівняння, яке має «зручні» коефіцієнти, тому розв’яжемо його за теоремою Вієта.

Крок 5

Перевіримо, чи задовольняють отримані корені ОДЗ рівняння.

 задовольняє ОДЗ

не задовольняє ОДЗ

Кр

ок

Зміст дії

Результат дії

Розкладемо знаменники дробовораціональних виразів на множники

Крок 1

Знайдемо область допустимих значень рівняння 

Крок 2

Перенесемо дробово-раціональний вираз 

   у ліву частину рівняння з

протилежним знаком. Зведемо до спільного знаменника дроби та виконаємо дію віднімання раціональних дробів з однаковими знаменниками

Крок 3

Скористаємося правилом рівності дробу нулю:

. З урахуванням

ОДЗ розглянемо рівність чисельника нулю. 

Помножимо обидві частини рівняння  на (-1)

Крок 4

Визначимо коефіцієнти отриманого квадратного рівняння. 

Це зведене квадратне рівняння, яке має «зручні» коефіцієнти, тому розв’яжемо його за теоремою Вієта.

Крок 5

Перевіримо, чи задовольняють отримані корені ОДЗ рівняння.

 задовольняє ОДЗ

не задовольняє ОДЗ