Додавання і віднімання дробів з різними знаменниками
Тема. Додавання і віднімання дробів з різними знаменниками
Мета: домогтися закріплення учнями змісту алгоритмів зведення раціональних дробів до спільного знаменника та додавання (віднімання) раціональних дробів з різними знаменниками; сформувати вміння свідомого виконання дій відповідно до вивчених алгоритмів; вдосконалити вміння виконувати перетворення раціональних дробів за алгоритмами, вивченими на попередніх уроках (скорочення раціональних дробів, застосування правила знаків, зведення до нового знаменника).
Тип уроку: застосування знань та вмінь.
Наочність та обладнання: опорний конспект «Додавання і віднімання раціональних дробів».
Хід уроку
I. Організаційний стан
II. Перевірка домашнього завдання
Для перевірки засвоєння учнями змісту алгоритму та вмінь зводити раціональні дроби до спільного знаменника можна організувати роботу з перевірки домашнього завдання за зразком (у парах) або провести роботу з відшукання помилок (учитель заздалегідь готує розв'язання домашніх вправ з «помилками», які учні мають відшукати). Зрозуміло, що в цьому разі проводиться перевірка та корекція виконаних учнями робіт одразу після її завершення.
III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів
Створенню відповідної мотивації навчальної діяльності учнів сприятиме усвідомлення проблем, сформульованих на попередньому уроці, а саме: зведення раціональних дробів до спільного знаменника не є самоціллю — це лише засіб, за допомогою якого додавання і віднімання будь-яких раціональних дробів можна виконувати за правилом додавання та віднімання раціональних дробів з однаковим знаменником. Свідоме сприйняття учнями цих тверджень приводить до розуміння того, що важливим постає питання про вивчення алгоритму додавання та віднімання раціональних дробів із різними знаменниками — це і с основна дидактична мета уроку, — а також допомагає окреслити коло завдань на урок: на основі вивчених алгоритмів додавання і віднімання раціональних дробів з однаковими знаменниками та зведення раціональних дробів до спільного знаменника сформулювати алгоритм додавання і віднімання раціональних дробів з різними знаменниками, а також сформувати первинні вміння застосовувати сформульований алгоритм для розв'язування відповідних завдань.
(Цей коментар має місце у випадку, коли на попередньому уроці було опрацьовано лише навчальний матеріал, що стосується зведення раціональних дробів до спільного знаменника. В іншому випадку метою уроку є закріплення вивченого на попередньому уроці порядку дій під час зведення раціональних дробів до спільного знаменника та виконання додавання та віднімання раціональних дробів із різними знаменниками).
IV. Актуалізація опорних знань та вмінь
Для успішної роботи учнів на уроці перед, початком вивчення основного питання слід поновити знання та вміння щодо виконання арифметичних дій з раціональними числами, дій зі степенями з натуральним показником, перетворень цілих виразів, а також перетворень раціональних дробів, що розглядатись на початку вивчення теми (скорочення раціональних дробів, знаходження ОДЗ раціональних дробів, застосування правила знаків та зведення раціонального дробу до нового знаменника).
Виконання усних вправ
-
Обчисліть:
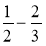 ;
; 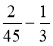 ;
; 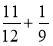 .
.
- Який вираз слід підставити замість *, щоб утворилася тотожність?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
- Подайте у вигляді добутку: т2 – п2; 4m2 – п2; т2 – 2тп + п2; mп – п2;
т2n – mn2; 5m2 – 10mn + 5n2.
- Знайдіть найменший спільний знаменник для дробів:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]() ;
;
г) ![]() і
і ![]() .
.
V. Застосування знань
Якщо на попередньому уроці вивчалося лише питання про зведення раціональних дробів до нового знаменника, то єдиним новим моментом цього уроку є запис алгоритму додавання та віднімання раціональних дробів з різними знаменниками, а також розгляд прикладів його застосування в типових ситуаціях.
Доведення тотожностей, що виражають правила додавання та віднімання раціональних дробів з різними знаменниками, спираються на основну властивість дробу та правила додавання і віднімання раціональних дробів з однаковими знаменниками. Всі міркування докладно подані в підручнику, тому вчитель на свій розсуд або пропонує учням самостійно за підручником опрацювати цей матеріал, або здійснює доведення під час фронтальної бесіди.
Формулювання і доведення алгоритму додавання і віднімання раціональних дробів з різними знаменниками обов'язково має завершитись демонстрацією його застосування. Тому після доведення алгоритму слід так само ретельно опрацювати приклади його застосування. Цю роботу також можна провести із використанням уміщених у тексті підручника прикладів: бажано організувати роботу так, щоб учні виділяли в розв'язанні послідовні кроки, записані в алгоритмі (тобто усвідомили послідовність виконаних дій). У будь-якому разі учні мають вивчити не тільки запис алгоритму у вигляді формули, але й отримати опис орієнтовної схеми дій у стандартних ситуаціях.
У роботі над вивченням цього питання, як і на попередньому уроці, вчитель звертається до опорного конспекту (див. урок №5).
VI. Застосування вмінь
Виконання усних вправ
-
Зведіть дріб
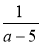 до знаменника: 5 – а; 2а – 10; а(а – 5); 25 – а2; а3 – 125.
до знаменника: 5 – а; 2а – 10; а(а – 5); 25 – а2; а3 – 125.
- Закінчіть виконання дій:
а) ![]() ; б)
; б) 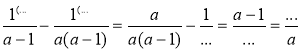 .
.
-
Подайте у вигляді дробу вираз: а)
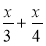 ; б)
; б) 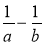 ; в)
; в) 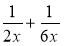 ; г)
; г) 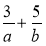 ;
;
д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
Виконання письмових вправ
Для реалізації дидактичної мети уроку на цьому уроці слід розв'язати завдання такого змісту.
- Додавання та віднімання раціональних дробів, з попереднім зведенням їх до нового знаменника.
1) Зведіть до спільного знаменника дроби:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]() ;
;
г) ![]() і
і ![]() ; д)
; д) ![]() і
і ![]() ; є)
; є) ![]() і
і ![]() .
.
2) Перетворіть у дріб вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
3) Перетворіть у дріб вираз: а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
4) Спростіть вираз: а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ; д)
; д) 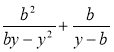 ;
;
є) ![]() ; ж)
; ж) 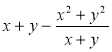 ; з)
; з) ![]() .
.
-
Доведення тотожностей (виконання перетворення суми або різниці
раціональних дробів у раціональний дріб).
1) Доведіть тотожність:
а) ![]() ; б)
; б) ![]() .
.
2) Доведіть тотожність:
а) 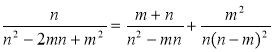 ; б)
; б) ![]() .
.
-
Знаходження значення виразу з попереднім спрощенням його, із
застосуванням алгоритмів додавання або віднімання раціональних
дробів з різними знаменниками.
Знайдіть значення виразу: а) ![]() при х = 4;
при х = 4;
б) ![]() при а = -2; b = 3.
при а = -2; b = 3.
- Виконання логічних вправ та завдань підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) При яких натуральних п значення виразу є натуральним числом:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ?
?
2) Знайдіть значення виразу, знаючи, що ![]() :
:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3) Вставте пропущений вираз:
|
5а – 3b |
2а + b |
3а – 4b |
|
|
|
? |
Вправи, запропоновані до розв'язання на уроці, мають відповідати за змістом прикладам, розв'язаним у підручнику, але з поступовим ускладненням, а саме:
- за рахунок збільшення кількості перетворень для пошуку спільного знаменника;
- збільшення кількості перетворень після зведення дробів до нового знаменника та запису їх суми або різниці у вигляді дробу (скорочення дробів та застосування правила знаків).
Вчителеві слід ясно уявляти собі, що перетворення суми (різниці) раціональних дробів приводить до раціонального виразу, тотожному до даного виразу на спільному ОДЗ даного і здобутого виразів, що співпадає з ОДЗ даного виразу (на цей факт слід звертати увагу учнів, бо він використовуватиметься надалі під час розв'язування раціональних рівнянь; зрозуміло, що вимагати від усіх учнів розуміння таких вказівок зарано).
Перетворюючи суми або різниці раціональних дробів у дріб, учні можуть пропонувати різні форми запису відповіді (наприклад відповідь виду ![]() записувати як
записувати як ![]() ), тобто необов'язково у вигляді дробу. Тому слід вказати учням на відмінність таких форм запису, хоча самі вирази тотожно рівні (перший вираз є раціональним дробом, другий є алгебраїчною сумою цілого виразу та раціонального дробу), а звідси — на необхідність усвідомлення учнями змісту завдання, яке вони беруться виконувати.
), тобто необов'язково у вигляді дробу. Тому слід вказати учням на відмінність таких форм запису, хоча самі вирази тотожно рівні (перший вираз є раціональним дробом, другий є алгебраїчною сумою цілого виразу та раціонального дробу), а звідси — на необхідність усвідомлення учнями змісту завдання, яке вони беруться виконувати.
VII. Підсумки уроку
Серед рівностей виберіть правильну. Поясніть свій вибір.
Тестове завдання
В якому з випадків правильно виконано додавання? В інших випадках укажіть помилку.
1) ![]() ;
;
2) ![]() ;
;
![]()
![]() 3)
3) 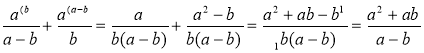 ;
;
4) 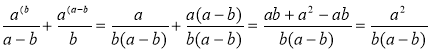 .
.
VIII. Домашнє завдання
- Вивчити правило додавання та віднімання дробів з різними знаменниками (з доведенням) та алгоритм (схему дій) під час його застосування.
- Розв'язати вправи репродуктивного характеру на застосування вивченого алгоритму.
- На повторення: завдання, що передбачають повторення правил скорочення дробів, застосування правила знаків та знаходження ОДЗ дробового виразу.


про публікацію авторської розробки
Додати розробку
