Розробка уроку на тему «Раціональні вирази. Раціональні дроби. Основна властивість дробу, додавання і віднімання раціональних дробів».
Тема. Підсумковий урок
Мета: повторити, систематизувати та узагальнити знання і способи дій, які опанували учні під час вивчення теми «Раціональні вирази. Раціональні дроби. Основна властивість дробу, додавання і віднімання раціональних дробів».
Тип уроку: систематизація та узагальнення знань і вмінь.
Наочність та обладнання: опорні конспекти № 1 – 3.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
З метою економії часу ретельній перевірці підлягають лише вправи на застосування алгоритму, вивченого на попередньому уроці (або зібрати зошити з виконаною домашньою самостійною роботою № 2).
III. Формулювання мети і завдань уроку, мотивація навчальної діяльності учнів
Основна дидактична мета та завдання на урок цілком логічно випливають із місця уроку в темі - оскільки урок є останнім, підсумковим, то актуальним постає питання про повторення, узагальнення та систематизацію знань та вмінь, набутих учнями в ході вивчення теми. Таке формулювання мети створює відповідну мотивацію діяльності учнів.
IV. Повторення та систематизація знань
Залежно від рівня підготовки, вчитель може організувати роботу учнів різними способами: або як самостійну роботу з теоретичним матеріалом (наприклад, за підручником або за конспектом теоретичного матеріалу повторити зміст основних понять теми, або ж скласти схему, що відображає логічний зв'язок між основними поняттями теми, тощо), або традиційно провести опитування (у формі інтерактивної вправи) за основними питаннями теми.
Виконання усних вправ
- Які вирази називають цілими? Наведіть приклади.
- Які вирази називають дробовими? Наведіть приклади.
-
Які вирази називають раціональними? Які з наведених раціональних виразів цілі? Які дробові? 3а;
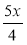 ; 15р2q;
; 15р2q; 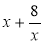 ;
; 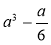 ;
; 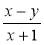 .
.
- Які значення змінних, що входять до виразу, називають допустимими значеннями?
- Як формулюється основна властивість дробу?
- Що відбувається зі знаком дробу, якщо змінити знак його чисельника і знаменника; чисельника; знаменника?
- Як додати дроби з однаковими знаменниками? Наведіть приклади.
- Як виконати віднімання дробів з однаковими знаменниками? Наведіть приклади.
- Як знайти спільний знаменник поданих раціональних дробів? Наведіть приклади.
-
Як додати (відняти) дроби з різними знаменниками? Розкажіть на прикладі дробів: а)
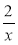 і
і 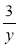 ; б)
; б) 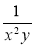 і
і 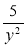 .
.
-
Як додати (відняти) раціональний дріб і цілий вираз? Покажіть це на прикладі виразів
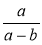 і а – b.
і а – b.
V. Повторення та систематизація вмінь
Зазвичай цей етап уроку проводиться у формі групової роботи, мета якої полягає в тому, щоб учні самі сформулювали та випробували узагальнену схему дій, якої вони мають дотримуватись, розв'язуючи типові завдання, подібні до яких будуть винесені на контроль.
Наприклад, типовими завданнями теми «Раціональні вирази» є завдання:
- Скоротити раціональні дроби.
- Перетворити в раціональний дріб суму або різницю двох або більшого числа раціональних виразів.
- Знайти допустимі значення змінної в раціональному виразі.
- Довести, що значення раціонального виразу, що дорівнює сумі або різниці раціональних дробів (із цілими виразами), не залежить від значення змінної, що міститься в цьому виразі.
- Знайти значення раціонального виразу при деякому значенні змінної (або виразів зі змінними).
Після складання списку основних видів завдань учитель формує робочі групи учнів (за кількістю видів завдань) і завдання кожної з груп формулюється так: «Скласти алгоритм розв'язання завдання...» (кожна з груп отримує індивідуальне завдання). На складання алгоритму кожній із груп відводиться певний час, за який учасники групи мають скласти алгоритм, записати його у вигляді послідовних кроків, підготувати презентацію своєї роботи. По закінченні відбувається презентація виконаної роботи кожною з груп. Після презентації - обов'язкове випробування алгоритмів: причому бажано, щоб групи обмінялись алгоритмами і перевірили їх застосування не на одному, а на кількох завданнях. Після випробування — обов'язкова корекція та підбиття підсумків.
VI. Підсумки уроку
Підсумком уроку узагальнення та систематизації знань і вмінь учнів є, по-перше, складені самими учнями узагальнені схеми дій під час розв'язування типових завдань, по-друге — здійснення учнями необхідної частини свідомої розумової діяльності учнів — рефлексії — відображення кожним учнем власного сприйняття своїх успіхів, та найголовніше — проблеми, над якими слід ще попрацювати.
VII. Домашнє завдання
- Вивчити складені на уроці алгоритми.
- Використовуючи складені алгоритми, виконати завдання домашньої контрольної роботи № 1.
Домашня контрольна робота
-
Скоротіть дроби: а)
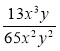 ; б)
; б) 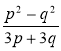 ; в)
; в) 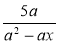 .
.
-
Подайте у вигляді дробу вирази: а)
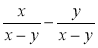 ; б)
; б) 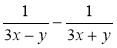 ;
;
в) ![]() ; г)
; г) 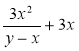 ; д)
; д) ![]()
-
Спростіть вираз
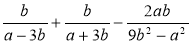 .
.
- Знайдіть значення виразу:
а) ![]() при а =
при а = ![]() ; х =
; х = ![]() ; б)
; б) ![]() при
при ![]() = 3.
= 3.
-
Доведіть, що при всіх допустимих значеннях а вираз тотожно дорівнює нулю:
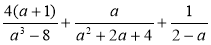 .
.
-
Знайдіть допустимі значення змінної у виразі
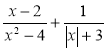 .
.


про публікацію авторської розробки
Додати розробку
