Додавання і віднімання дробів з різними знаменниками
Тема. Додавання і віднімання дробів з різними знаменниками
Мета: домогтися закріплення учнями змісту алгоритмів зведення раціональних дробів до спільного знаменника та додавання (віднімання) раціональних дробів з різними знаменниками; вдосконалити вміння свідомого виконання дій відповідно до вивчених алгоритмів, перетворення раціональних Дробів за алгоритмами, вивченими на попередніх уроках (скорочення раціональних дробів, застосування правила знаків, зведення до нового знаменника).
Тин уроку: застосування знань, відпрацювання вмінь.
Наочність та обладнання: опорний конспект «Додавання і віднімання раціональних дробів».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Оскільки вправи домашнього завдання є вправами репродуктивного (в основному) характеру, то перевірку домашнього завдання можна здійснити або частково (тільки в учнів, що потребують додаткової педагогічної уваги), або можна запропонувати учням перевірити відповіді (правильні відповіді заздалегідь записані за дошкою або роздані як картки для самостійного опрацювання).
III. Формулювання мети і завдань уроку, мотивація навчальної діяльності учнів
Для усвідомлення учнями необхідності вивчення матеріалу, запропонованого на цьому уроці, можна створити проблемну ситуацію: розглянувши спочатку завдання на перетворення суми або різниці цілого числа і звичайного дробу у звичайний дріб (матеріал відомий із 6 класу) та за умови успішного виконання цього завдання, відповісти на запитання:
- Чи можливе подібне перетворення під час роботи з раціональними виразами?
- Якщо це так, то за яким алгоритмом слід виконувати дії в цьому разі?
Зрозуміло, що за умови усвідомлення учнями існування аналогій між алгоритмами скорочення, додавання та віднімання звичайних та раціональних дробів, на останні два запитання дасться ствердна відповідь, а це дозволяє свідомо (можливо із залученням учнів) сформулювати як основну дидактичну мету уроку — алгоритм додавання та віднімання цілих і дробових раціональних виразів та засвоєння навичок його застосування, — так і завдання на урок: застосовуючи вміння, набуті підчас вивчення теми «Додавання і віднімання раціональних дробів», навчитись розв'язувати більш складні завдання.
IV. Актуалізація опорних знань та вмінь
Перед початком вивчення питання щодо виконання сумісного додавання або віднімання цілих і дробових раціональних виразів слід активізувати знання та вміння учнів стосовно виконання таких дій: арифметичні дії зі звичайними дробами, подання цілого числа у вигляді дробу із заданим знаменником, перетворення суми або різниці раціональних дробів з однаковими знаменниками на раціональний дріб, скорочення раціональних дробів, зведення раціонального дробу до нового знаменника.
Виконання усних вправ
-
Обчисліть:
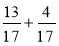 ;
; 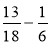 ;
; 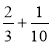 ;
; 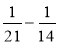 ;
; 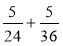 .
.
-
Подайте у вигляді дробу вирази: 2; 2,5; 2
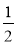 ; а; а + 1; 3а2 – а + 1.
; а; а + 1; 3а2 – а + 1.
- Розкладіть на множники вираз: 25 – х2; a2 + ab; 8 + а3; 1 + х2 – 2х;
3х6 – 12х4; b10 – b6.
- Перетворіть у дріб вираз:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() ; и)
; и) ![]() .
.
- Заключіть у дужки вирази, перед якими стоїть знак «–»:
а – b; а + b; а - b + с; – а – b; – 2а – 2b + с.
V. Застосування знань
У роботі над складанням алгоритму додавання та віднімання цілих раціональних виразів і раціональних дробів слід підкреслити: по-перше, на відміну від додавання або віднімання цілих чисел зі звичайними дробами (коли перевага надається виконанню дій без перетворення цілого числа у неправильний дріб), у роботі з раціональними виразами подібний спосіб виконання дій просто неможливий. По-друге, якщо цілий вираз є многочленом, то бажано цей многочлен подати у вигляді одного дробу, причому якщо цей многочлен є від'ємником, то, перш ніж подавати його у вигляді дробу, слід заключити його в дужки, перед якими стоїть знак мінус. По-третє, щоб правильно виконати названі вище дії, необхідно чітко виконувати послідовність дій, передбачених вивченим алгоритмом додавання і віднімання раціональних дробів з різними знаменниками (до цього алгоритму додається лише один крок: записати поданий цілий вираз у вигляді дробу зі знаменником 1). (Див. опорний конспект).
VI. Застосування вмінь
Виконання усних вправ
- Запишіть у вигляді дробу зі знаменником а – b вирази:
1; 3; a; ab; a + b; a2 + ab + b2; а – b.
- Закінчіть виконання дій:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) ![]() .
.
Виконання письмових вправ
Для реалізації дидактичної мети уроку слід розв'язати завдання такого змісту.
- Перетворення на раціональний дріб суми (різниці) цілого виразу та раціонального дробу.
1) Виконайте додавання (віднімання) дробів:
а) ![]() ; б)
; б) ![]() ; в)
; в)  .
.
2) Спростіть вираз: а) 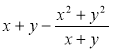 ; б)
; б) ![]() .
.
3) Перетворіть у дріб вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; є)
; є) 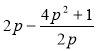 ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
4) Подайте у вигляді дробу: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
5) Перетворіть у дріб вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
- Спрощення виразів, що містять додавання або віднімання раціональних виразів (як цілих, так і дробових).
1) Доведіть, що при будь-яких допустимих значеннях змінної значення виразу:
а) ![]() є додатним числом;
є додатним числом;
б) 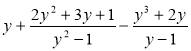 є від'ємним числом.
є від'ємним числом.
2) Доведіть, що вирази тотожно рівні:
а) ![]() і
і ![]() ; б)
; б) ![]() і а – 1.
і а – 1.
3) Подайте у вигляді дробу: а) ![]() ;
;
б) ![]() ; в)
; в) 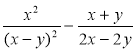 ; г)
; г) ![]() .
.
-
Виконання вправ на повторення: вправи на повторення способів
дій, вивчених на попередніх уроках (на скорочення раціональних дробів, зведення раціональних дробів до нового знаменника, знаходження ОДЗ раціонального дробу, знаходження значень змінної, при яких значення раціонального дробу дорівнює нулю).
1) Скоротіть дріб:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) 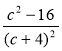 ; д)
; д) ![]() ;
;
є) 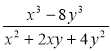 ; ж)
; ж) 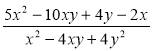 .
.
2) Знайдіть значення виразу ![]() при а = 25; а = -1,8.
при а = 25; а = -1,8.
3) Спростіть вираз: а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
4) Подайте у вигляді суми або різниці цілого виразу і дробу:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
- Виконання логічних вправ та завдань підвищеного рівня складності для учнів, які мають достатній та високий рівень знань.
1) Доведіть, що коли при деяких натуральних значеннях а і b дріб ![]() нескоротний, то й дріб
нескоротний, то й дріб ![]() нескоротний.
нескоротний.
2) Спростіть вираз:
а) ![]() ;
;
б) 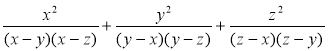 .
.
Оскільки урок є останнім у розділі «Додавання і віднімання раціональних дробів з різними знаменниками», крім завдань на закріплення алгоритму додавання та віднімання цілого виразу і раціонального дробу (особливу увагу слід приділити випадкам віднімання від раціонального дробу многочлена), для розв'язання пропонується низка завдань на відпрацювання навичок, набутих на попередніх уроках розділу, та на повторення алгоритмів скорочення дробів та знаходження ОДЗ дробового виразу.
VII. Підсумки уроку
Самостійна робота № 2
(можна запропонувати як домашню самостійну роботу)
Варіант 1
Подайте у вигляді дробу вирази:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) 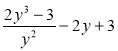 .
.
Варіант 2
Подайте у вигляді дробу вирази:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) 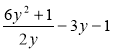 .
.
VIII. Домашнє завдання
- Розв'язати вправи на додавання і віднімання раціональних дробів з однаковими і різними знаменниками і раціональних дробів з цілими виразами.
- На повторення: розв'язати вправи на скорочення дробів і знаходження ОДЗ раціональних виразів.
- Повторити алгоритми виконання вивчених дій з раціональними дробами.


про публікацію авторської розробки
Додати розробку
