Додавання та віднімання многочленів

Тема. Додавання та віднімання многочленів

Мета: вдосконалити вміння учнів перетворювати суму та різницю многочленів у многочлен стандартного вигляду; виробити вміння викону­вати обернені перетворення (заключати кілька членів многочлена в дуж­ки, перед якими стоїть певний знак); здійснити проміжну діагностику рівня засвоєння знань та вмінь.

Тип уроку: застосування знань, умінь та навичок.

Хід уроку

І. Перевірка домашнього завдання

 № 1 (1, 2) та № 2, № 3 домашнього завдання — це вправи на закріп­лення знань та вмінь, вироблення яких було розпочато на попередньо­му уроці. Тому вчитель або організовує само- та взаємоперевірку, або розбирає під час фронтальної бесіди незрозумілі моменти.

№ 1 (3) потребує більшої уваги, бо це завдання, що містить у собі «дужки в дужках». Тому цю вправу обов'язково перевіряємо (роботи учнів, які впоралися із цим завданням, можуть бути оцінені).

Пояснюючи, слід звернути увагу: оскільки ми володіємо правилами розкриття дужок, перед яким стоїть знак «+» або «–», то й починаємо з того, що шукаємо «внутрішні» дужки, які можна розкрити за названими правилами, і, якщо можна, зводимо подібні члени.

Після цього процес повторюється доти, доки ми не перетворимо де­який вираз у вираз, що зовсім не містить дужок. (Робимо запис (див. ниж­че) і коментуємо кожний крок.)

(2а³ – 6b³) – (2а³ – 6аb – (5а³ – (3аb + 7b³))).

1-й крок: 2а³ – 6b³ – (2а³ – 6ab – (5a³ – 3аb – 7b³)) ...

2-й крок: 2а³ – 6b³ – (2а³ – 6ab – 5a³ + 3ab + 7b³) ...

3-й крок: 2а³ – 6b³ – (–3а³ – 3ab + 7b³) ...

4-й крок: 2а³ – 6b³ + 3а³ + 3аb – 7b³ ...

5-й крок: 5а³ + 3аb – 13b³.

II. Актуалізація опорних знань

 Цей етап уроку проводимо у вигляді бесіди, але бажано для усві­домлення учнями своїх дій, щоб не вчитель ставив учням запитання (що традиційно робимо на етапі актуалізації), а щоб учні самі під­бирали ці запитання, а потім записували відповідь на них. Щоб зорієн­тувати учнів на пошук у правильному напрямку, можна скористатися підказкою-прикладом № 1 (3) з домашнього завдання (було обговоре­но раніше). Запитання, які ставить учитель, можуть бути такими:

Розглянувши приклад № 1 (3) з домашнього завдання, з'ясуйте:

1. Вираз якого вигляду було перетворено?
2. Які види перетворень (і за якими алгоритмами) було виконано на кожному кроці перетворень?

III. Робота з випереджальним домашнім завданням

 Оскільки приклади, з якими працювали учні вдома, можуть бути різними, пропонуємо загальні приклади:

1) (х + 2у) + (2х – у) = х + 2у + 2х – у; 2) (х + 2у) – (2х – у) = х + 2у – 2х + у.

Учням пропонуємо самостійно попрацювати за таким алгоритмом:

1. Запишіть дані тотожності у зворотному порядку (поміняйте місцями праву та ліву частину рівності).
2. Порівняйте праву та ліву частину кожної з новоутворених рівностей (за алгоритмом порівняння).
3. Зробіть висновок.

По закінченні роботи учні презентують свої наробки, і проводиться корекція та узагальнення висновків, а отже, формулюємо правила:

1. Якщо перед дужками стоїть знак «+», то члени, що беруть у дужки, записують з тими ж самими знаками.
2. Якщо перед дужками стоїть знак «–», то члени, що беруть у дужки, за­писують із протилежними знаками.

IV. Узагальнення знань. Засвоєння та розширення вмінь

 Перед виконанням вправ акцентуємо на тому, що ми маємо у своє­му арсеналі правила (алгоритми) 2-х взаємообернених дій:

1. додавання та віднімання многочленів;
2. заключення членів многочлена в дужки.

Але при цьому перетворення дещо схожі, тобто залежно від знака, що стоїть перед дужками, знаки доданків у дужках або не змінюються, або змінюються на протилежні. Тому роботу з виконання обох видів завдань починаємо саме з визначення знака перед дужками.

Виконання усних вправ

1. Обчисліть: 57 – 29; 57 – 89; –5,7 + 2,9;  5,7 – 29; 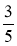 – 0,4; – 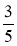– 0,4.
2. Чи правильна рівність? Якщо ні, знайдіть та виправі є помилку.

1) (–5х² + 2ху – 4) + (4х² – 6ху) = –5х² + 2ху – 4 – 4х² – 6ху;

2) (–5а² + 1) – (8а² + 4аb) = –5а² – 1 + 8а² – 4аb;

3) 3а² – 7а + 1 = 3а² – (–7а – 1);

4) = а ∙ b ∙ а ∙ (а²b).

3. Розв'яжіть рівняння: х – 0,3 = 5; x + 0,3 = –5.

Яким правилом, відомим вам з молодшої школи, ви користувалися?

Виконання письмових вправ

1. Знайдіть значення виразу:

12х² – (5х² + 2ху) – (7х² – 4ху), якщо х = 0,35; у = 4.

2. Замість (*) поставте такий многочлен, щоб утворилася тотожність:

1) (*) – (5ху – х² + 2у²) = 3х² + ху;  2) 5а³ – а² + 3а⁴ – 7 + (*) = 2а² – 3а.

3. Доведіть, що значення виразу (7п + 2) – (4п – 7) кратне 3 при будь-якому натуральному п.                                          

4*. Доведіть, що різниця чисел: і ділиться на 9.

5. Подайте   многочлен   8а² + 5b – 7а³ + 11а – 6  у   вигляді   різниці   двох многочленів так, щоб один з них не містив змінної b.

6*. Подайте многочлен –2х² + 3х – 5 у вигляді різниці двох двочленів.

V. Діагностика засвоєння знань та вмінь

Самостійна робота

VI. Підсумок уроку

Проведення самоперевірки та самоцінювання виконаних робіт (за запропонованими вчителем підказками правильною розв'язування вправ).

VII. Домашнє завдання

(Замість виконання № 1 та 2 можна запропонувати учням виконати аналіз самостійної роботи.)

№ 1. Який многочлен у сумі з многочленом 5х² – 3х – 9 тотожно дорівнює:

1) 0;   2)18;  3) 2х – 3;  4) х² – 5х + 6?

№ 2. Доведіть, що вираз (2х⁶ – 4х² – 2) – (х – х² – 3) + (3х² + х) набуває тільки додатних значень при будь-яких значеннях х. Якого найменшого значення набуває цей вираз і при якому значенні х?

№ 3. Випереджальне домашнє завдання.

Послідовно виконайте такі завдання:

1) Повторіть зміст понять «одночлен», «многочлен», «члени многочле­на», «розподільна властивість множення».

2) Яке з названих понять можна використати, щоб записати вирази, то­тожно рівні виразам: a(b + c); a(b – c); a(b + c + d)?

3) Використовуючи слова «одночлен», «добутки», «многочлен», «члени многочлена», «сума», прочитайте тотожність, що утворилася в п. 2.