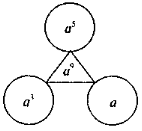
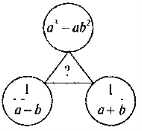
Раціональні рівняння. Розв'язування раціональних рівнянь
Тема. Раціональні рівняння. Розв'язування раціональних рівнянь
Мета: домогтися засвоєння учнями змісту схем розв'язання дробово-раціональних рівнянь із використанням основної властивості пропорції та властивості рівносильних рівнянь; закріпити знання учнів щодо вивчених на попередньому уроці понять (раціональне рівняння, ціле рівняння, дробово-раціональне рівняння, ОДЗ рівняння та схеми розв'язання дробового рівняння виду ![]() = 0, де А і В — деякі многочлени від однієї змінної); сформувати вміння застосовувати вивчені схеми для розв'язування рівнянь відповідного виду, вдосконалити вміння виконувати вивчені на попередніх уроках перетворення раціональних виразів.
= 0, де А і В — деякі многочлени від однієї змінної); сформувати вміння застосовувати вивчені схеми для розв'язування рівнянь відповідного виду, вдосконалити вміння виконувати вивчені на попередніх уроках перетворення раціональних виразів.
Тип уроку: доповнення знань, удосконалення вмінь.
Наочність та обладнання: опорний конспект «Додавання та віднімання раціональних дробів».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Одним зі способів перевірки рівня засвоєння учнями знань та вмінь, запропонованих для вивчення на попередньому уроці, є математичний диктант.
Математичний диктант
- Закінчіть речення:
Рівняння називають раціональним, якщо....
- Закінчіть речення:
Рівняння називають цілим раціональним рівнянням, якщо...
- Складіть та запишіть два дробово-раціональних рівняння різного виду
-
Розв'яжіть рівняння
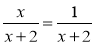 .
.
Якщо під час розв'язування вправ домашнього завдання учні мали значні труднощі, тоді доцільно провести перевірку домашнього завдання за зразком.
ІІІ. Формулювання мети і завдань уроку
З метою усвідомлення учнями необхідності вивчення матеріалу, запропонованого на поточний урок, учитель може провести роботу, що передбачає розв'язування учнями завдань на виконання таких розумових дій, як порівняння (знаходження спільного та відмінного), а також узагальнення та формулювання гіпотези.
Виконання усних вправ
- Розгляньте рівняння:
1) ![]() ; 2)
; 2) 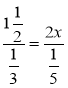 ; 3)
; 3) ![]() ; 4)
; 4) ![]()
та порівняйте їх за різними критеріями (видом самого рівняння, видом виразів, з яких складаються права та ліва частини рівнянь, тощо). Що в них спільного, відмінного? Яким способом розв'язуються перші два рівняння? Чи можна третє і четверте рівняння розв'язати таким способом? Що додатково слід врахувати, розв'язуючи останні два рівняння?
- Розгляньте рівняння:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
та порівняйте їх за різними критеріями (видом самого рівняння, видом виразів, з яких складаються права та ліва частини рівнянь, тощо). Що в них спільного, відмінного? Яким способом розв'язуються перші два рівняння? Чи можна третє і четверте рівняння розв'язати таким способом? Що додатково слід врахувати, розв'язуючи останні два рівняння?
Після проведеної роботи учні мають сформулювати питання (проблему) — чи не можна дробово-раціональні рівняння, що мають вигляд пропорції або рівності раціональних виразів, розв'язувати подібними способами — до способів розв'язання цілих раціональних рівнянь відповідного вигляду? Які додаткові дії при цьому обов'язково слід виконати? Пошук відповіді на поставлене запитання і становить основну дидактичну мету уроку, до якої додаються завдання: сформулювати алгоритми розв'язання дробово-раціональних рівнянь із застосуванням основної властивості пропорції та властивості рівносильних рівнянь (якщо обидві частини рівняння помножити на одне й те саме число, відмінне від нуля, то дістанемо рівняння, рівносильне даному), а також, закріпивши знання послідовності дій, передбачених цими алгоритмами, сформувати вміння застосовувати ці алгоритми на практиці (для розв'язування відповідного виду рівнянь).
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчального матеріалу перед вивченням матеріалу уроку слід активізувати такі знання і вміння учнів: тотожні перетворення цілих виразів; перетворення суми, різниці, добутку і частки двох раціональних дробів на раціональний дріб; знаходження спільного знаменника для даних кількох раціональних дробів; застосування основної властивості пропорції та властивості рівносильних рівнянь.
Виконання усних вправ
- Виконайте дії:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
- Знайдіть спільний знаменник для дробів:
![]() і
і ![]() ;
; ![]() і
і ![]() ;
; ![]() і
і ![]() ;
; ![]() і
і ![]() .
.
-
Розв'яжіть рівняння:
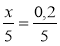 ;
; 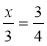 ;
; 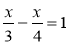 ;
; 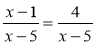 .
.
V. Засвоєння знань
План вивчення нового матеріалу
- Алгоритм розв'язання дробово-раціонального рівняння, що має вигляд пропорції (із прикладом).
- Алгоритм розв'язання дробово-раціонального рівняння, що має вигляд рівності двох раціональних виразів (із прикладом).
Розв'язування учнями завдань на етапі формулювання мети і завдань уроку підготувало учнів до свідомого сприйняття ними змісту навчального матеріалу уроку: схеми розв'язання дробово-раціональних рівнянь із застосуванням основної властивості пропорції та із використанням властивості рівносильних рівнянь.
Перед вивченням першого питання плану слід розглянути питання про ОДЗ дробового рівняння виду ![]() : учні мають усвідомити, що в цьому випадку ОДЗ знаходимо з умови В ≠ 0, D ≠ 0. Тоді алгоритм розв'язання рівнянь типу
: учні мають усвідомити, що в цьому випадку ОДЗ знаходимо з умови В ≠ 0, D ≠ 0. Тоді алгоритм розв'язання рівнянь типу ![]() можна записати у вигляді такої схеми дій:
можна записати у вигляді такої схеми дій:
- Знайти ОДЗ рівняння (див. попередній урок).
- Використати основну властивість пропорції: перейти до рівняння AD = BC, розв'язати це рівняння.
-
Перевірити, які зі знайдених коренів задовольняють ОДЗ; ті, що не
задовольняють ОДЗ, є сторонніми коренями; записати відповідь.
Після складання схеми дій необхідно проілюструвати її застосування під час розв'язування відповідного прикладу.
Під час вивчення питання про спосіб переходу від дробового рівняння, що має вигляд рівності двох раціональних виразів, до цілого рівняння, можна запропонувати учням перетворення, що ґрунтується на застосуванні властивості рівносильних рівнянь – у результаті множення обох частин рівняння на вираз, що не дорівнює нулю, утворюється рівняння, рівносильне даному (такий спосіб розв'язання цілих рівнянь схожого вигляду учні вивчили в 7 класі). Так само, як і за перетворення цілих рівнянь, таким множником є спільний знаменник для всіх дробів, але спільний знаменник у випадку дробового рівняння є виразом зі змінними. Тому ОДЗ такого дробового рівняння знаходимо з умови: спільний знаменник усіх дробів не дорівнює нулю.
Після цього формулюється загальна схема дій розв'язування дробових рівнянь:
- знайти спільний знаменник усіх раціональних дробів; знайти ОДЗ рівняння (див. вище);
- помножити обидві частини рівняння на спільний знаменник; розв'язати утворене ціле рівняння;
- виконати перевірку знайдених коренів цілого рівняння на відповідність їх до ОДЗ (див. п. 1), відсіяти можливі сторонні корені, записати відповідь.
Підбиваючи підсумки вивченого матеріалу, слід зауважити, що вивчені схеми розв'язання дробових рівнянь відрізняються лише способом переходу до цілого рівняння, серед коренів якого можуть міститися корені даного дробового рівняння; загальні положення розв'язання дробових рівнянь є незмінними: перейшовши до цілого рівняння (яке є наслідком даного рівняння) та розв'язавши це ціле рівняння, обов'язково враховуємо ОДЗ даного дробового рівняння або перевіряємо, чи не перетворюють корені цілого рівняння знаменник даного рівняння на нуль.
Слід зауважити, що оволодіти бажано всіма трьома видами перетворень, бо існують види рівнянь, розв'язання одних з яких простіше зробити одним способом, ніж іншим (доречно було б це проілюструвати на прикладах).
VI. Засвоєння вмінь
Виконання усних вправ
- При яких значеннях змінної а не мають змісту вирази:
![]() ;
; ![]() ;
; ![]() ?
?
- Чи рівносильні рівняння:
а) ![]() та 3х = 2(х – 1); б)
та 3х = 2(х – 1); б) ![]() та х(х + 3) = (х – 1)(х + 1)?
та х(х + 3) = (х – 1)(х + 1)?
Чому?
- При якому значенні х значення дробів рівні:
![]() і
і ![]() ;
; ![]() і
і ![]() ;
; ![]() і
і ![]() ;
; ![]() і
і ![]() ?
?
Виконання письмових вправ
Щоб реалізувати дидактичну мету, на цьому уроці слід розв'язати завдання такого змісту:
-
Розв'язування дробово-раціональних рівнянь за алгоритмами
(складеними на уроках 20, 21).
1) Розв'яжіть рівняння:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) 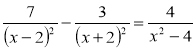 ;
;
е) 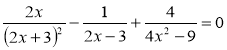 .
.
-
Складання та розв'язування (найбільш раціональним способом)
дробово-раціональних рівняння за умовою задачі.
1) Відстань між містами А і В дорівнює 720 км. З міста А до міста В виїхав автомобіль і одночасно з ним вилетів літак. Автомобіль прибув до міста В на 10 год пізніше від літака. Знайдіть швидкість літака та автомобіля, якщо швидкість літака в 6 разів більша від швидкості автомобіля.
2) До басейну підведено дві труби. Через першу трубу басейн можна наповнити водою удвічі швидше, ніж через другу. Якщо відкрити обидві труби одночасно, то басейн наповниться за 4 год. За який час можна наповнити басейн через кожну трубу окремо?
-
На повторення: перетворити раціональний вираз із використанням
набутих раніше знань.
1) Спростіть вираз: а) 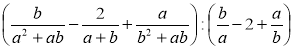 ;
;
б) 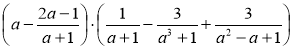 ; в)
; в) 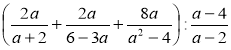 .
.
2) Доведіть тотожність: а) 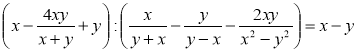 ;
;
б) 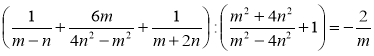 .
.
- Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Який вираз пропущено?
|
|
|
|a| ≠ |b| |
5.* Розв'язування дробово-раціонального рівняння з параметром.
1) Розв'яжіть рівняння з параметром а: ![]() .
.
2) При яких значеннях а рівняння ![]() не має коренів?
не має коренів?
3) При яких значеннях а рівняння ![]() має один корінь?
має один корінь?
Усні вправи сприяють закріпленню учнями схеми дій під час виконання перетворень відповідно до певного алгоритму і а формуванню первинних умінь виконувати дії відповідно до вивчених алгоритмів.
Під час розв'язування письмових вправ на уроці слід вимагати від учнів дотримування правил: перед розв'язуванням дробового рівняння визначити вид рівняння, а вже потім вибрати відповідний спосіб рівносильних перетворень рівняння; вибравши певний алгоритм перетворень дробового рівняння, слід чітко слідувати тільки цьому алгоритму, не «перескакувати» на інший; рівняння вважається розв'язаним тільки якщо виконана вся послідовність дій, передбачена алгоритмом.
VII. Підсумки уроку
В якому з випадків правильно розв'язане рівняння?
|
а) (2х – 3)(х – 1) = (2х – 1)(х + 3), 2х2 + 3 = 2х2 – 3, 3 = -3 — коренів немає |
б)
1) ОДЗ: 2х – 1 ≠ 0 та х - 1 ≠ 0; 2) (2х – 3)(х – 1) = (2х – 1)(х + 3), 2х2 - 3х – 2х + 3 = 2х2 – х + 6х – 3, - 5х + 3 = 5х - 3, -10х = -6, х = 0,6 — задовольняє ОДЗ. 3) Відповідь. 0,6 |
VIII. Домашнє завдання
- Вивчити алгоритми розв'язання дробово-раціональних рівнянь різного вигляду; скласти загальний алгоритм розв'язання дробово-раціональних рівнянь.
- Розв'язати дробово-раціональні рівняння та вправи, що передбачають складання та розв'язування дробово-раціональних рівнянь.
- Повторити вивчені схеми дій під час перетворення раціональних виразів; розв'язати вправи на застосування цих схем та вивчених раніше способів перетворення окремого виду раціональних виразів.


про публікацію авторської розробки
Додати розробку