«Додавання векторів. Множення вектора на число. Кут між векторами. Скалярний добуток векторів»
Тестові завдання на тему:
«Додавання векторів. Множення вектора на число. Кут між векторами. Скалярний добуток векторів»
Мета тесту: здійснити тематичне оцінювання навчальних досягнень учнів 9 класу загальноосвітньої школи з теми: «Додавання векторів. Множення вектора на число. Кут між векторами. Скалярний добуток векторів».
Тест містить 20 завдань, із них: 10 завдань з вибором 1 правильної відповіді; 3 завдання на встановлення відповідності; 1 завдання на встановлення правильної послідовності; 4 завдання з короткою відповіддю; 2 завдання з розгорнутою відповіддю.
Максимальна кількість балів за тест – 34.
Час виконання – 45 хвилин.
Матриця тесту
Умовні позначення:
ВОВ – завдання з вибором 1 правильної відповіді
ВВ – завдання на встановлення відповідності
ВП – завдання на встановлення правильної послідовності
КВ – завдання з короткою відповіддю
РВ – завдання з розгорнутою відповіддю
|
Підтема |
I – початковий рівень |
II – середній рівень |
III – достатній рівень |
IV – високий рівень |
Загальна к-сть завдань |
|
1.Додавання векторів. |
3 ВОВ 1, 2. Розуміння правила трикутника для додавання векторів. 3. Розуміння правила паралелограма для додавання векторів. |
1 ВВ 11. Вміння виражати вектор через суму і різницю двох векторів |
1 КВ 15. Вміння знаходити суму і різницю двох векторів, їх модуль. |
– |
5 |
|
2. Множення вектора на число. |
1 ВОВ 4. Вміння визначати напрямленість векторів через означення добутку вектора на число. |
1 ВОВ 5. Вміння обчислювати добуток вектора на число, якщо заданий модуль вектора. 1 ВВ 12. Вміння обчислювати добуток вектора на число та його модуль, якщо задані координати вектора. |
1 ВП 14. Вміння застосовувати вивчені означення до доведення теорем. 1 КВ 16. Вміння знаходити значення координати одного вектора за умови його колінеарності з другим вектором. |
– |
5 |
|
3. Кут між векторами. |
3 ВОВ 6, 7, 8. Вміння знаходити із рисунка кут між векторами. |
– |
1 КВ 17. Вміння знаходити значення кута між двома векторами. |
1 РВ 19. Вміння застосовувати вивчені означення до розв’язування задач (обчислення координатів та модуля вектора, косинуса кута між двома векторами). |
5 |
|
4. Скалярний добуток векторів. |
2 ВОВ 9. Вміння визначати за значенням скалярного добутку вид кута між векторами. 10. Вміння формулювати умову перпендикулярності двох векторів. |
1 ВВ 13. Вміння обчислювати скалярний добуток двох векторів. |
1 КВ 17. Вміння знаходити скалярний добуток двох векторів та косинус кута між ними. |
1 РВ 20. Вміння застосовувати вивчені означення до розв’язування задач (обчислення скалярного квадрата та скалярного добутку двох векторів). |
5 |
|
|
9 |
4 |
5 |
2 |
20 |
ЗАВДАННЯ З ВИБОРОМ ОДНІЄЇ ПРАВИЛЬНОЇ ВІДПОВІДІ
Завдання 1-10 мають по чотири варіанти відповідей, серед яких лише одна правильна. Правильно виконане завдання оцінюється 1 балом.
1. Дано трикутник АВС. Виразіть вектор 
через вектори 
і 
.
а) + ; в) – ;
б) – ( + ); г)
– .
2. Дано трикутник АВС. Виразіть вектор через вектори і
.
а) – ; в) –
;
б) + ; г) 
–.
3. Дано паралелограм АВСD. Виразіть вектор через вектори і
.
а) –; в)
+;
б) +; г) – ( +).
4. Який з векторів співнапрямлений з вектором 
, якщо 
?
а) –3; в) 
;
б) 
; г) 3.
5. Знайдіть модуль вектора 
, якщо 
= 6.
а) –3; в) 
;
б) 
; г) 3.
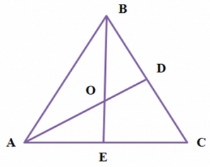
6. На рисунку 1 зображено рівносторонній трикутник АВС, медіани якого AD і ВЕ перетинаються в точці О. Знайдіть кут між векторами 
і .
а) 45°; в) 90°;
б) 60°; г) 180°.
7. На рисунку 1 зображено рівносторонній трикутник АВС, медіани якого AD і ВЕ перетинаються в точці О. Знайдіть кут між векторами і 
.
а) 60°; в) 120°;
б) 90°; г) 180°.
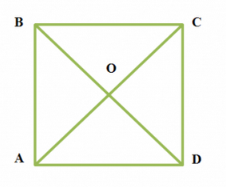
8. На рисунку 2 зображено квадрат АВСD, діагоналі якого перетинаються в точці О. Знайдіть кут між векторами і .
а) 30°; в) 90°;
б) 45°; г) 135°.
9. Відомо, що скалярний добуток векторів є від’ємним числом. Вичначте вид кута між векторами.
а) гострий; в) тупий;
б) прямий; г) розгорнутий.
10. Скалярний добуток двох ненульових векторів дорівнює нулю тоді й тільки тоді, коли ці вектори:
а) рівні; в) колінеарні;
б) перпендикулярні; г) протилежно напрямлені.
ЗАВДАННЯ НА ВСТАНОВЛЕННЯ ВІДПОВІДНОСТІ
Завдання 11-13 передбачають встановлення відповідності. За кожну правильно позначену логічну пару можна отримати 0,5 бали. Максимальна кількість балів за повністю правильно виконане завдання становить 2 бали.
11. Точки М і N – середини відповідно сторін ВА і ВС трикутника АВС; 
= 
, 
= 
. Встановіть відповідність між векторами (1–4) та їх вираженням через і (А–Д).
|
1. |
А. |
|
2. |
Б. |
|
3. |
В. |
|
4. |
Г. |
|
|
Д. |
12. Дано вектор (–6; 12). Встановіть відповідність між векторами (1–4) та їх модулями (А–Д).
|
1. |
А. |
|
2. |
Б. |
|
3. |
В. |
|
4. |
Г. |
|
|
Д. |
13. Встановіть відповідність між векторами (1–4) та їх скалярними добутками (А–Д).
|
1. |
А. 0 |
|
2. |
Б. 2 |
|
3. |
В. 3 |
|
4. |
Г. 4 |
|
|
Д. 6 |
ЗАВДАННЯ НА ВСТАНОВЛЕННЯ ПОСЛІДОВНОСТІ
Завдання 14 передбачає установлення послідовності. Максимальна кількість балів за правильно виконане завдання становить 2 бали.
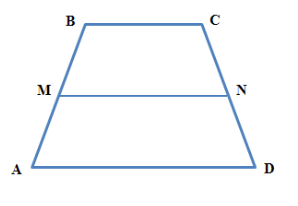14. Встановіть послідовність доведення теореми про середню лінію трапеції за допомогою векторів, користуючись рисунком 3.
|
А. |
|
Б. |
|
В. |
|
Г. |
|
|
ЗАВДАННЯ З КОРОТКОЮ ВІДПОВІДДЮ
За правильно виконане завдання з короткою відповіддю Ви отримуєте 2 бали; за неправильно виконане або взагалі не виконане завдання Ви отримуєте 0 балів.
15. Дано вектори 
(4; -5), 
(-1; 7). Знайдіть:
1) координати векторів + , + ;
2) 
, 
.
16. Знайдіть значення х, при якому вектори (2; 3) і 
(-1; х) колінеарні.
17. Знайдіть кут між векторами і , якщо ( + 3)( – ) = –11, =2, 
=3.
18. Дано вектори (1; -2), (2; -3). Знайдіть:
1) скалярний добуток векторів і .
2) косинус кута між векторами і .
ЗАВДАННЯ З РОЗГОРНУТОЮ ВІДПОВІДДЮ
За правильно виконане завдання з розгорнутою відповіддю максимально Ви отримуєте 4 бали; за взагалі не виконане завдання Ви отримуєте 0 балів.
19. Знайдіть кути трикутника з вершинами А(0; 6), В(4
; 6), С(3; 3).
20. У трикутнику АВС АВ = 4 см, ВС = 6 см, 
= 30°. Знайдіть довжину медіани ВМ.
Відповіді:
1. Завдання з вибором однієї правильної відповіді
Відповіді:
|
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
10. |
|
а |
в |
б |
г |
г |
в |
в |
г |
в |
б |
2. Завдання на встановлення відповідності
Відповіді:
11.1-Г, 2-В, 3-А, 4-Д.
12.1-В, 2-Г, 3-Д, 4-Б.
- 1-Г, 2-Б, 3-В, 4-А.
3. Завдання на встановлення послідовності
Відповіді:
14.1-Д, 2-А, 3-В, 4-Г, 5-Б.
4. Завдання з короткою відповіддю
15. Відповідь:
+ = (
, + = (
; = 
, = 13.
16. Відповідь: х = –1,5.
17. Відповідь: 
=0°.
18. Відповідь: · = 8; 
= 
.
19. Критерії оцінювання:
|
І етап (1 бал): Знаходимо координати векторів |
||
|
|
|
|
|
ІI етап (1 бал): Знаходимо модулі векторів: |
||
|
|
|
|
|
ІII етап (1 бал): Знаходимо скалярні добутки: |
||
|
|
|
|
|
IV етап (0,5 бала):
Знаходимо косинуси кутів |
||
|
|
|
|
|
V етап (0,5 бала): Знаходимо третій кут: |
||
|
|
|
|
|
Відповідь: 30°, 60°, 90°. |
||
20. Критерії оцінювання:
І етап (1 бал):
За правилом паралелограма, 
ІI етап (1 бал):
Знаходимо квадрат медіани:
.
ІII етап (1 бал):
Записуємо одержану рівність із використанням скалярного квадрату і скалярного добутку:
.
IV етап (1 бал):
Знаходимо ВМ:
; ВМ2 = 49; ВМ = 7 (см).
Відповідь: 7 см.
Шкала переводу тестових балів в оцінку за 12-бальною системою:
|
Тестові бали |
Оцінка за 12-бальною шкалою |
|
1-3 |
1 |
|
4-6 |
2 |
|
7-10 |
3 |
|
11-13 |
4 |
|
14-15 |
5 |
|
16-17 |
6 |
|
18-20 |
7 |
|
21-23 |
8 |
|
24-27 |
9 |
|
28-30 |
10 |
|
31-32 |
11 |
|
33-34 |
12 |
Харківський національний педагогічний університет імені Г.С.Сковороди
Тестові завдання на тему:
«Додавання векторів. Множення вектора на число. Кут між векторами. Скалярний добуток векторів»
|
Залікове завдання |
|
з основ педагогічних вимірювань |
|
та моніторингу якості освіти |
|
студентки ІV курсу МФ групи |
|
фізико-математичного факультету |
|
Назаренко Валерії Володимирівни |
Харків – 2017
про публікацію авторської розробки
Додати розробку