Домашня контрольна робота з геометрії за I семестр 7 класу

Домашняя контрольная работа по геометрии

за I семестр  7 класс

Домашняя контрольная работа по геометрии

за I семестр  7 класс

Вариант 1

Вариант  2

1.  Зная, что АВ — 8, М — середина отрезка АВ, найдите на пря­мой АВ все такие точки X, для которых сумма ХА+ХВ+ХМ равна 9. Покажите эти точки на рисунке.

1. Зная, что АВ — 8, М — середина отрезка АВ, найдите на пря­мой АВ все такие точки X, для которых сумма ХА +ХВ+ ХМ равна 15. Покажите эти точки на рисунке.

2. Прямой угол двумя лучами, исходящими из его вершины, разделён на три угла, один из которых равен разности двух других углов. Найдите величину большего из этих углов.

2. Прямой угол разделен лучом, исходящим из его вершины, на два таких угла, что половина одного угла равна трети другого. Найдите эти углы.

3. При пересечении двух прямых один из образовавшихся углов в 8 раз меньше суммы остальных углов. Найдите величину каждого из этих углов.

3. При пересечении двух прямых один из образовавшихся углов равен суммы  остальных углов. Найдите величину каждого из этих углов.

4. На рисунке 1 ВЕ и СF — высоты треугольника АВС. При помощи только линейки постройте высоту АХ этого треугольника. Найдите длину отрезка ВС, если АХ = ВЕ, СХ=СЕ  и  АС = 17 дм.

4. На рисунке 1 КР и МF — высоты треугольника КМL. При помощи только линейки постройте высоту LХ этого треугольника. Найдите величину угла ХLМ, если  КР = LХ_,  МР=МХ и РКМ = 27⁰.

5. 1) На рисунке 2 треугольник ABC равнобедренный с основанием АС, L – середина АС, АМ = СК. Докажите, что МL=LK.

5. 1) На рисунке 2 изображён равнобедренный треугольник с основанием РТ, СО – высота треугольника, РВ = ТА. Докажите, что РВО = ОАТ. 

2) Равнобедренные треугольники АВС и DBC имеют общее основание ВС. Вершины А и D находятся по разные стороны от ВС. Отрезки AD и ВС пересекаются в точке О. Докажите, что ADВС.

2) Равнобедренные треугольники АВС и АВD имеют общее основание АВ. Вершины С и D находятся по разные стороны от АВ. Отрезки АВ и СD пересекаются в точке М. Докажите, что М – середина АВ.

6. 1) На одной стороне угла с вершиной А отмечены точки D и B, на другой стороне – С и E так, что

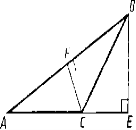
    АD = АС = 3 см,  АВ =АЕ = 4 см.  Докажите, что:

а) ВС = ЕD;

б) КВ = КЕ, где К — точка пересечения отрезков ВС и ED.

2) АВС и A₁В₁С₁ — равнобедренные треугольники с основа­ниями АС и А₁С₁, точки М и М₁ — середины сторон ВС и В₁С₁ соответственно,    АВ=А₁В₁,    АМ=А₁М₁.    Докажите,    что ΔАВС=ΔА₁В₁С₁.

6. 1) На одной стороне угла с вершиной В отмечены точки М  и  О, на другой — К  и  Р так, что ВМ = ВР,  ВО < ВМ, ВК < ВР, а ОРВ = КМВ. Докажите, что:

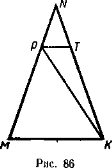
а) МК = ОР;

б) ТМ = ТР, где Т - точка пересечения отрезков МК и ОР.

2) АС  и А₁С₁ — основания  равнобедренных треугольников АВС и А₁В₁С₁, точки М  и  М₁ — середины сторон ВС и В₁С₁ соответственно,  АС = А₁С₁,  АВ = А₁В₁. Докажите, что  ΔАВМ = ΔА₁В₁М₁.

7. На рисунке 3 АВ = ВС, ЕD =АЕ, С ==80°,  DAС = 40^о.

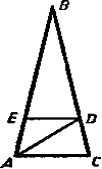
Докажите, что прямые ЕD и AС параллельны. Найдите угол

ВЕD.

7. На  рисунке 3  РN = NT,  РK — биссектриса угла  MРT, 

NРГ = 70°, РKM = 55°. Докажите, что прямые РT и MK параллельны. Найдите угол РКТ.

8. На отрезке АВ взята точка С; через точки А и В проведены по одну сторону от АВ параллельные лучи. На них отложены отрезки АО = АС и ВЕ = ВС, точка С соединена отрезками с точками D и E. Докажите, что DССЕ.

8. Через точку О, расположенную внутри треугольника АВС, проведена прямая DЕ, параллельная стороне АС и пересекающая стороны АВ и ВС соответственно в точках D и Е. АD = DО и СЕ—ЕО. Докажите, что ВО –  биссектриса угла АВС.