Допоміжний матеріал до уроку «Ознаки зростання і спадання функції»

Допоміжний матеріал до уроку «Ознаки зростання і спадання функції»

Дорогі десятикласники!

Сьогодні я наведу вам ще декілька прикладів на застосування ознак зростання (спадання) функції.

№22.3(1,3)

 1).  f(х) = – – 7;

= = – = –  = х( – 1) =

=х(х – 1)(х + 1);

  = 0,   х(х – 1)(х + 1) = 0,   х = 0, х = – 1, х = 1 –  точки,                       в яких похідна змінює (може змінювати) знак.

Ці точки розбивають числову пряму на проміжки:

; ; ; .

Визначаємо знак похідної на кожному з утворених проміжків в довільно взятих точках:

= (–5)(– 5–1)(–5 +1) = –120, тобто на проміжку

х є; функція є спадною.

= (–0,5)(–0,5 –1)(–0,5 + 1) =0,375, тобто на проміжку

х є задана функція є зростаючою, і т.д.

Одержані знаки відмічаємо на числовому промені:

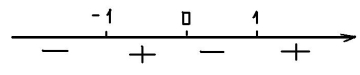
Отже, функція (зростає), якщо хє і хє; .

Функція (спадає), якщо хє; і хє.

3). f(х) = + ;

= =  = 2х – 2   = 2х – = =

=  ;        =  0,  х = 1. Але в даному випадку є ще точка

х 0  , тобто утворилися проміжки: (– );  (0 ; ; .  

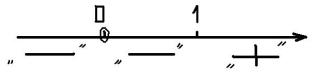
Отже, функція (зростає), якщо хє; .

Функція (спадає), якщо хє; 0)  і  х є (0;

Бажаю успіху!

Б а ж а ю МИРУ!